- •Сборник задач по оптике
- •Содержание
- •Часть I. Геометрическая оптика и фотометрия
- •Законы отражения и преломления света. Принцип Ферма.
- •Построение изображений в сферическом зеркале.
- •Построение изображения в тонкой линзе
- •Оптические приборы. Микроскоп и телескоп.
- •Элементы матричной оптики. Толстые линзы.
- •Фотометрия
- •Часть II. Плоскополяризованный свет. Формулы френеля.
- •Часть III. Интерференция света
- •Часть IV. Дифракция
- •Дифракция Френеля. Зонная пластинка
- •Дифракция Фраунгофера. Дифракционная решетка.
- •Разрешающая способность оптических приборов.
- •Часть V. Молекулярная оптика и смежные разделы
- •Элементы кристаллооптики. Эллиптически поляризованный свет.
- •Дисперсия света. Фазовая и групповая скорости.
- •Давление света
- •Тепловое излучение
- •Список литературы
Элементы матричной оптики. Толстые линзы.
|
|
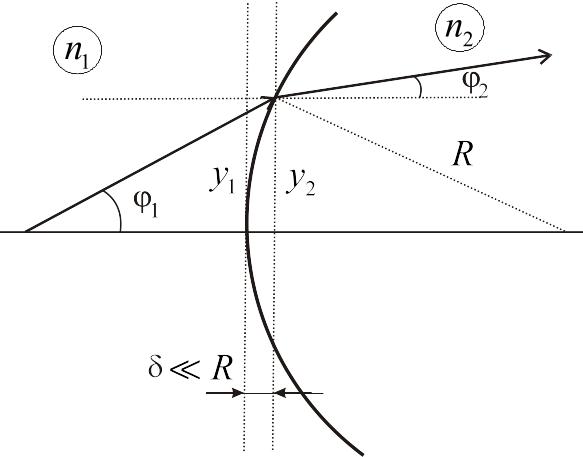
Рис.15. К получению преломляющей матрицы |
Рис.16. К получению передаточной матрицы |
Любой луч в рамках гауссовой оптики можно определить заданием двух параметров: координаты
 и углом наклона к оптической оси
.
и углом наклона к оптической оси
.
Преломляющая матрица – матрица, описывающая преобразование параметров луча света, преломляющегося на сферической разделяющей поверхности радиуса (рис. 15):
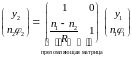 .
.
Преломляющая сила (оптическая сила) преломляющей сферической разделяющей поверхности:
 .
.
Передаточная матрица – матрица, описывающая преобразование параметров луча света, распространяющегося в оптически однородном промежутке (рис. 16):

Здесь
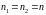 ,
,
 .
.
Получить выражение для преломляющей и передаточной матрицы.
Получить матрицу
 преобразования параметров параксиального
луча для толстой линзы.
преобразования параметров параксиального
луча для толстой линзы.
|
Рис. 17 |
 .
Причём в рамках гауссовой оптики
расстояние
можно измерять вдоль оптической оси
(рис 17). Поэтому матрица
получается путём перемножения преломляющих
матриц двух сферических границ раздела
(с оптическими силами
.
Причём в рамках гауссовой оптики
расстояние
можно измерять вдоль оптической оси
(рис 17). Поэтому матрица
получается путём перемножения преломляющих
матриц двух сферических границ раздела
(с оптическими силами
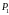 и
и
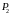 )
и матрицы оптического промежутка.
)
и матрицы оптического промежутка.
Ответ:
 .
.
Покажите, что матрица, описывающая распространение луча из области предметов через толстую линзу в область изображений, может быть представлена в виде
 ,
,
где
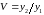 – линейное поперечное увеличение линзы,
– линейное поперечное увеличение линзы,
 .
Указание:
Как и в предыдущей задаче, перемножьте
в нужном порядке матрицу толстой линзы
и передаточные матрицы в пространстве
предметов и изображений. Используйте
затем свойство стигматичности изображения,
а также тот факт, что
.
Указание:
Как и в предыдущей задаче, перемножьте
в нужном порядке матрицу толстой линзы
и передаточные матрицы в пространстве
предметов и изображений. Используйте
затем свойство стигматичности изображения,
а также тот факт, что
 .
.
Найдите положение главных плоскостей
 и
и
 толстой линзы. Ответ:
Положение передней главной плоскости
толстой линзы. Ответ:
Положение передней главной плоскости
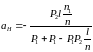 относительно полюса первой разделяющей
поверхности, положение задней главной
плоскости
относительно полюса первой разделяющей
поверхности, положение задней главной
плоскости
 относительно полюса второй разделяющей
поверхности. Значение координаты левее
полюса считается отрицательной.
относительно полюса второй разделяющей
поверхности. Значение координаты левее
полюса считается отрицательной.Найдите положение фокальных плоскостей
 и
и
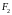 толстой линзы. Ответ:
Положение передней фокальной плоскости
толстой линзы. Ответ:
Положение передней фокальной плоскости
 относительно полюса первой разделяющей
поверхности, положение задней фокальной
плоскости
относительно полюса первой разделяющей
поверхности, положение задней фокальной
плоскости
 относительно полюса второй разделяющей
поверхности.
относительно полюса второй разделяющей
поверхности.Выразите фокусные расстояния толстой линзы через оптические силы ее преломляющих поверхностей. Ответ:
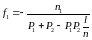 ,
,
 .
.
-
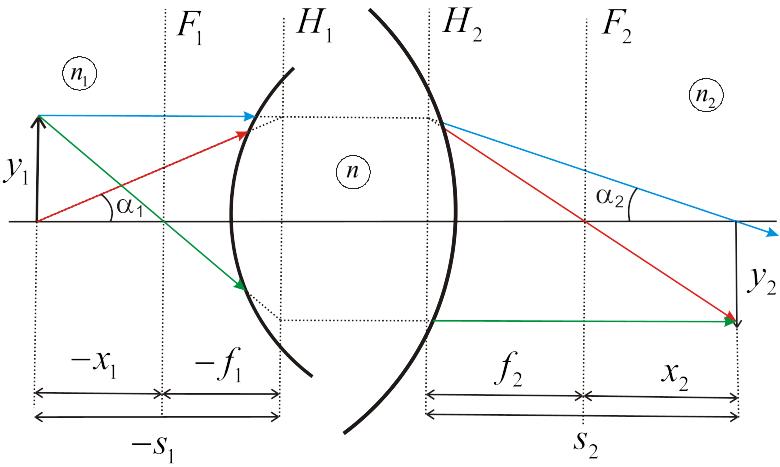
Рис. 18. К определению формулы толстой линзы.
Используя рис. 18, получить
уравнение толстой линзы в форме Гаусса:
 ;
;уравнение толстой линзы в форме Ньютона:
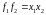 ;
;теорему Лагранжа-Гельмгольца:
 (углы отмеряют против часовой стрелки,
расстояние вертикально вверх).
(углы отмеряют против часовой стрелки,
расстояние вертикально вверх).
Найдите связь между угловым
 и поперечным увеличением
толстой
линзы. Ответ:
и поперечным увеличением
толстой
линзы. Ответ:
 .
.Как связаны между собой угловое, поперечное и продольное
 увеличения толстой линзы?
Ответ:
увеличения толстой линзы?
Ответ:
 .
.Можно ли в оптической системе получить и линейное и угловое увеличение одновременно?
Используя выражение для фокусного расстояния толстой линзы (см. задачу 46), по обе стороны от которой находится одно и то же вещество с
 ,
получите оптическую силу толстой и
тонкой линзы. Ответ:
,
получите оптическую силу толстой и
тонкой линзы. Ответ:
 ,
,
 .
Если луч встречает на своём пути выпуклую
сферическую разделяющую поверхность,
то радиус кривизны считается положительным.
Для тонкой линзы полагаем
.
Если луч встречает на своём пути выпуклую
сферическую разделяющую поверхность,
то радиус кривизны считается положительным.
Для тонкой линзы полагаем
 .
.Найти фокусное расстояние
 двояковыпуклой тонкой линзы, ограниченной
сферическими поверхностями с радиусами
двояковыпуклой тонкой линзы, ограниченной
сферическими поверхностями с радиусами
 мм и
мм и
 мм; показатель преломления стекла линзы
мм; показатель преломления стекла линзы
 .
Ответ:
31 мм.
.
Ответ:
31 мм.Используя решение задачи 45, найти оптическую силу тонкой линзы (показатель преломления ), погружённой в среду с показателем преломления
 .
Ответ:
.
Ответ:
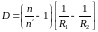 .
.Линза с фокусным расстоянием
 см сделана из стекла с показателем
преломления
.
Найти фокусное расстояние
см сделана из стекла с показателем
преломления
.
Найти фокусное расстояние
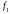 линзы, помещенной в воду с показателем
преломления
линзы, помещенной в воду с показателем
преломления
 .
Ответ:
.
Ответ:
 .
.Две тонкие симметричные линзы с одинаковыми радиусами кривизны преломляющих поверхностей
 см (одна – собирающая, с показателем
преломления
см (одна – собирающая, с показателем
преломления
 ,
а другая –
рассеивающая,
с показателем преломления
,
а другая –
рассеивающая,
с показателем преломления
 )
прижали вплотную друг к другу и погрузили
в воду с
)
прижали вплотную друг к другу и погрузили
в воду с
 .
Найти фокусное расстояние f
этой
оптической системы.
.
Найти фокусное расстояние f
этой
оптической системы.
Ответ:
 см.
см.
Оптическая система находится в воздухе. Пусть ОО' – ее оптическая ось, f и
 –
передний и задний фокусы, Н
и Н'
– передняя
и задняя главные плоскости, Р
и Р'
– сопряженные
точки. Найти построением:
–
передний и задний фокусы, Н
и Н'
– передняя
и задняя главные плоскости, Р
и Р'
– сопряженные
точки. Найти построением:
а) положение
 и Н'
(рис. а);
и Н'
(рис. а);
б) положение точки S', сопряженной с точкой S (рис.б);
в) положение F, F' и Н' (рис. в, где показан ход луча до и после прохождения системы).
-
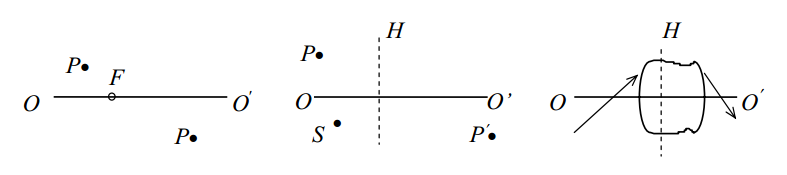
Рис.19
Две тонкие линзы с фокусными расстояниями
 и
и
 находятся на расстоянии
друг от друга, образуя центрированную
систему. Найти фокусное расстояние
этой системы, а также положения ее
главных плоскостей. Ответ:
находятся на расстоянии
друг от друга, образуя центрированную
систему. Найти фокусное расстояние
этой системы, а также положения ее
главных плоскостей. Ответ:
 расстояния главных плоскостей системы
от первой и второй линз соответственно
равны
расстояния главных плоскостей системы
от первой и второй линз соответственно
равны
 ,
,
 .
.В каком случае двояковыпуклая линза, изготовленная из стекла с показателем преломления и находящаяся в воздухе, будет рассеивающей? Ответ: Когда толщина линзы
 ,
где
,
где
 и
и
 – абсолютные
значения радиусов кривизны поверхностей
линзы.
– абсолютные
значения радиусов кривизны поверхностей
линзы.Найти положения главных плоскостей и фокусные расстояния для центрированной системы, состоящей из одной сферической преломляющей поверхности. Ответ: Главные плоскости совпадают между собой и касаются преломляющей поверхности в точке пересечения ее с главной оптической осью;
 .
.Имеются две тонкие симметричные линзы: одна собирающая с показателем преломления
 ,
другая рассеивающая с
,
другая рассеивающая с
 .
Обе линзы имеют одинаковый радиус
кривизны поверхностей
.
Обе линзы имеют одинаковый радиус
кривизны поверхностей
 см. Линзы сложили вплотную и погрузили
в воду
см. Линзы сложили вплотную и погрузили
в воду
 .
Каково фокусное расстояние этой системы
в воде? Ответ:
.
Каково фокусное расстояние этой системы
в воде? Ответ:
 см.
см.Стеклянный шар
 имеет радиус R
= 4
см. 1) Найти
расстояние
от центра шара до изображения предмета,
который находится на расстоянии 6 см
от поверхности шара. 2) Определить
линейное увеличение. Ответ:
1)
имеет радиус R
= 4
см. 1) Найти
расстояние
от центра шара до изображения предмета,
который находится на расстоянии 6 см
от поверхности шара. 2) Определить
линейное увеличение. Ответ:
1)
 см, 2) увеличение
см, 2) увеличение
 .
.Радиус кривизны
 сферической поверхности стеклянной
(
сферической поверхности стеклянной
( )
плоско-выпуклой линзы равен 26 см. Толщина
линзы
)
плоско-выпуклой линзы равен 26 см. Толщина
линзы
 см. Вычислить фокусное расстояние f
линзы и
найти положение изображения предмета,
расположенного на расстоянии 75 см от
выпуклой поверхности линзы. Ответ:
см. Вычислить фокусное расстояние f
линзы и
найти положение изображения предмета,
расположенного на расстоянии 75 см от
выпуклой поверхности линзы. Ответ:
 см; в 148 см от плоской поверхности.
см; в 148 см от плоской поверхности.На сколько радиус кривизны
 выпуклой поверхности выпукло-вогнутой
стеклянной
линзы толщиной
выпуклой поверхности выпукло-вогнутой
стеклянной
линзы толщиной
 см должен быть больше радиуса кривизны
вогнутой поверхности, чтобы в воздухе
линза была телескопической? Ответ:
см должен быть больше радиуса кривизны
вогнутой поверхности, чтобы в воздухе
линза была телескопической? Ответ:
 см.
см.Показать, что две тонкие линзы, сделанные из одного материала, образуют ахроматизированную в отношении фокусного расстояния систему, если расстояние между ними
 .
.Написать условие ахроматизации двух линз, сложенных вплотную. Какое заключение о фокусных расстояниях обеих компонент ахроматической линзы можно сделать из этого условия? Ответ:
 .
Фокусные расстояния обеих компонент
имеют всегда противоположные знаки.
Если вся система собирающая, то линза
с большей дисперсией рассеивающая, а
линза с меньшей дисперсией собирающая.
Наоборот, если система рассеивающая,
то линза с большей дисперсией должна
быть собирающей, а линза с меньшей
дисперсией – рассеивающей.
.
Фокусные расстояния обеих компонент
имеют всегда противоположные знаки.
Если вся система собирающая, то линза
с большей дисперсией рассеивающая, а
линза с меньшей дисперсией собирающая.
Наоборот, если система рассеивающая,
то линза с большей дисперсией должна
быть собирающей, а линза с меньшей
дисперсией – рассеивающей.