
- •Сборник задач по оптике
- •Содержание
- •Часть I. Геометрическая оптика и фотометрия
- •Законы отражения и преломления света. Принцип Ферма.
- •Построение изображений в сферическом зеркале.
- •Построение изображения в тонкой линзе
- •Оптические приборы. Микроскоп и телескоп.
- •Элементы матричной оптики. Толстые линзы.
- •Фотометрия
- •Часть II. Плоскополяризованный свет. Формулы френеля.
- •Часть III. Интерференция света
- •Часть IV. Дифракция
- •Дифракция Френеля. Зонная пластинка
- •Дифракция Фраунгофера. Дифракционная решетка.
- •Разрешающая способность оптических приборов.
- •Часть V. Молекулярная оптика и смежные разделы
- •Элементы кристаллооптики. Эллиптически поляризованный свет.
- •Дисперсия света. Фазовая и групповая скорости.
- •Давление света
- •Тепловое излучение
- •Список литературы
Дифракция Фраунгофера. Дифракционная решетка.
Используя метод Френеля-Кирхгофа, рассчитать дифракцию Фраунгофера на круглом отверстии радиуса . Длина волны , свет падает под углом
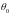 к нормали. Указание:
Используйте определение функции Бесселя
к нормали. Указание:
Используйте определение функции Бесселя
 .
Ответ:
.
Ответ:
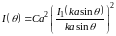 .
.Щель постоянной ширины прикрыта двумя плоскопараллельными стеклянными пластинками толщины с показателями преломления и , примыкающими друг к другу. Одна пластинка закрывает первую половину щели, другая – вторую половину щели. На щель нормально падает плоская монохроматическая волна с длиной волны . 1) Рассчитать распределение интенсивности на экране, если коэффициенты пропускания (по интенсивности) пластинок равны
 и
и
 .
2) При каком условии центр дифракционной
картины Фраунгофера будет темным?
Ответ:1)
.
2) При каком условии центр дифракционной
картины Фраунгофера будет темным?
Ответ:1)
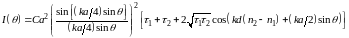 ,
где
,
где
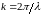 ,
2)
,
2)
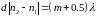 ,
,
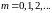
Одну половину длинной узкой щели шириной b перекрывают тонкой прозрачной пластиной с показателем преломления n. В результате интенсивность света в центре дифракционной картины уменьшается в два раза. Найти 1) толщину d пластины и 2) интенсивность света в направлениях, соответствующих направлениям на дифракционные минимумы в отсутствие пластины. Решите задачу аналитическим методом (см. предыдущую задачу) и методом векторных диаграмм. Поглощением в пластине пренебречь. Ответ:
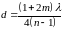 ,
,
,
,
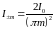 ,
если
– нечетное,
,
если
– нечетное,
 ,
если
– четное.
,
если
– четное.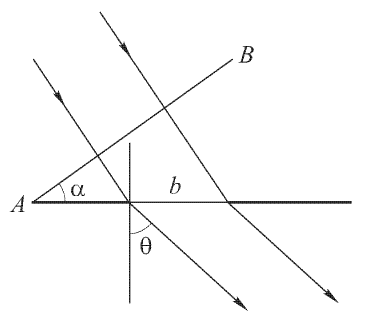
Рис.36
На щель ширины положена стеклянная призма с показателем преломления и преломляющим углом (см. рис.36). На грань АВ призмы нормально падает плоская монохроматическая волна. Найти направления на нулевой максимум и минимумы в дифракционной картине Фраунгофера. Ответ: Нулевой максимум
 ,
минимумы
,
минимумы
 .
.Плоская волна проходит через стеклянную пластинку с показателем преломления п, падая на ее поверхность нормально. Толщина пластинки испытывает скачкообразное изменение на величину d порядка длины световой волны вдоль некоторой прямой, проходящей через точку С перпендикулярно к плоскости рисунка (рис. 37). Прошедшая волна собирается линзой в ее фокусе. При каких значениях d интенсивность света в фокусе будет вдвое меньше интенсивности света в том же фокусе в случае отсутствия уступа на пластинке? Ответ:
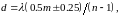 где
где
Найти угловое распределение интенсивности света при фраунгоферовой дифракции на решетке из N щелей и с периодом d при условии, что световые лучи падают на решетку нормально, а ширина щели равна b.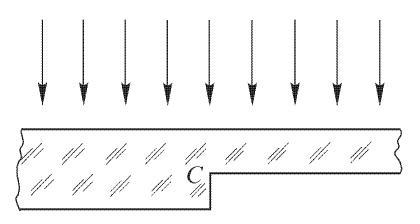
Рис. 37
Плоская монохроматическая волна с длиной падает нормально на простую дифракционную решетку. Дифракционная картина наблюдается в фокальной плоскости, установленной за решеткой собирающей линзы. Найти, как изменится дифракционная картина, если увеличить в два раза 1) число щелей N; 2) ширину щели (
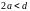 );
3) период решетки d;
4) длину волны
.
Как изменится дифракционная картина,
если свет буде падать на решетку под
углом
?
);
3) период решетки d;
4) длину волны
.
Как изменится дифракционная картина,
если свет буде падать на решетку под
углом
?
Показать, что для дифракционной решётки с периодом
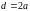 все чётные максимумы пропадают.
все чётные максимумы пропадают.На дифракционную решетку с периодом нормально падает параллельный пучок монохроматического света с длиной волны . Решетка имеет
 щелей шириной
щелей шириной
 каждая. Найти угловое распределение
интенсивности света за решеткой, если
закрыть центральную её часть непрозрачным
экраном так, что по краям решетки
открытыми остаются по
каждая. Найти угловое распределение
интенсивности света за решеткой, если
закрыть центральную её часть непрозрачным
экраном так, что по краям решетки
открытыми остаются по
 щелей. Ответ:
щелей. Ответ:
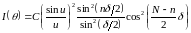 ,
где
,
где
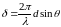 ,
,
 .
.Показать, что интенсивность света после прохождения экрана с отверстием произвольной формы
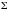 пропорциональна спектральной плотности
возмущения
пропорциональна спектральной плотности
возмущения
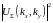 в плоскости дифракционного отверстия.
Здесь
в плоскости дифракционного отверстия.
Здесь
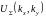 – фурье-образ поля
– фурье-образ поля
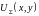 ,
проходящего через решётку.
,
проходящего через решётку.Рассчитать дифракцию Фраунгофера на щели с коэффициентом пропускания
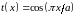 ,
где
– ширина щели, начало отсчёта находится
в центре щели. Угол падения света равен
.
Ответ:
,
где
– ширина щели, начало отсчёта находится
в центре щели. Угол падения света равен
.
Ответ:
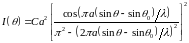 .
.Синусоидальная решетка с периодом и с амплитудным коэффициентом пропускания
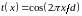 освещается нормально падающей плоской
волной. Найти распределение интенсивности
за синусоидальной решеткой. Рассмотреть
случаи, когда решетка имеет конечную
ширину L
и бесконечную ширину.
освещается нормально падающей плоской
волной. Найти распределение интенсивности
за синусоидальной решеткой. Рассмотреть
случаи, когда решетка имеет конечную
ширину L
и бесконечную ширину.
Рассчитать дифракционную картину отражательной фазовой решетки с периодом , изображенной на рис. 38. Ответ: Поле в точке наблюдения равно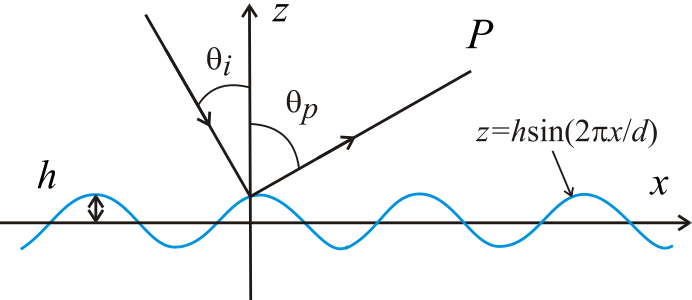
Рис.38.
 ,
где
,
где
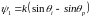 ,
,
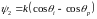 ,
,
,
,
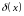 – функция Дирака. При
– функция Дирака. При
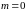
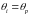 – угол блеска.
– угол блеска.
Дифракционная решетка имеет 1000 штрихов. Сколько штрихов должна иметь решетка, чтобы угловая ширина главного максимума уменьшилась в два раза? Ответ: 2000.
На дифракционную решетку нормально падает пучок света от разрядной трубки. Какова должна быть постоянная d дифракционной решетки, чтобы в направлении
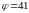 0
совпадали максимумы линий
0
совпадали максимумы линий
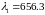 нм и
нм и
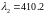 нм? Ответ:
нм? Ответ:
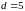 мкм.
мкм.
Могут ли перекрываться спектры первого и второго порядков дифракционной решетки при освещении ее видимым светом (400 –700 нм)? Ответ: нет.
Рис.39
Описать характер спектров дифракционной решетки, если ее постоянная равна: 1) удвоенной; 2) утроенной; 3) учетверенной ширине щели.
Рассчитать и проанализировать дифракционную картину при нормальном падении света на пилообразную решетку (см. рис. 39), сделанную из стекла с показателем преломления n. Число зубьев решетки равно N,
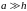 .
Длина волны падающего света равна
.
.
Длина волны падающего света равна
.Подсчитать минимальное число штрихов решетки, которая может разрешить натриевый дублет (
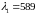 нм,
нм,
 нм) в спектре первого порядка. Ответ:
1000.
нм) в спектре первого порядка. Ответ:
1000.На дифракционную решетку падает нормально параллельный пучок белого света. Спектры третьего и четвертого порядка частично накладываются друг на друга. На какую длину волны в спектре четвертого порядка накладывается граница (
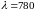 нм) спектра третьего порядка? Ответ:
585 нм.
нм) спектра третьего порядка? Ответ:
585 нм.Наблюдается дифракция параллельного пучка монохроматического излучения с частотой ν = 1015 Гц, падающего нормально па дифракционную решетку с числом штрихов N = 15000. Во сколько раз изменится угловая расходимость в 1-м порядке, если падающее на решетку излучение промодулировать так, чтобы были сформированы короткие импульсы длительностью τ = 10-12 с? Ответ: в 16 раз.
