ЭАиТЧ_ПР3_Наибольший общий делитель и его линейное представление. Наименьшее общее кратное

МИНОБРНАУКИ РОССИИ

Федеральное государственное образовательное учреждение высшего образования

“Юго–Западный государственный университет”

Кафедра информационной безопасности

Лабораторная работа №3

По дисциплине «Элементы алгебры и теории чисел»

По теме «Наибольший общий делитель и его линейное представление. Наименьшее общее кратное.»

Выполнил: студент группы ИБ-11б

Гребенникова А.И.

Проверил проф. Добрица В.П.

Курск 2023г.

Цель: изучить понятия НОД и НОК, их свойства, теорему Евклида о НОД, научиться находить линейное представление НОД.

Ход работы:

Вариант 5.

Задание1. Вычислить НОД d = (299; 391; 667) двумя способами

1. Разложим числа на простые множители

;

Из разложения видно, что НОД = 23.

2. Найдем все возможные делители чисел (299, 391, 667). Для этого поочередно разделим число 299 на делители от 1 до 299, число 391 на делители от 1 до 391, число 667 на делители от 1 до 667. Если число делится без остатка, то делитель запишем в список делителей.

Для числа 299 выпишем все случаи, когда оно делится без остатка:

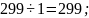
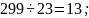
Для числа 391 выпишем все случаи, когда оно делится без остатка:

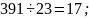
Для числа 667 выпишем все случаи, когда оно делится без остатка:

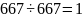
Выпишем все общие делители чисел (299, 391, 667) и выделим самый большой, это и будет наибольший общий делитель НОД чисел (299, 391, 667) Общие делители чисел (299, 391, 667): 1, 23

Ответ: НОД (299, 391, 667) = 23.

(Почему убираете мои замечания? Повторяю их.) Извиняюсь, видимо я пропустила письмо с вашим ответом, либо оно до меня не дошло по каким-то причинам, поэтому решила повторно отправить первоначальный вариант работы.

(Вы фактически 2 раза применили метод разложения на простые множители. А надо другой метод: последовательное нахождение НОД для двух чисел (в первом случае) и найденного НОД и третьего числа по алгоритму Евклида.)

Воспользуемся алгоритмом Евклида. Запишем его поэтапно соответствующими равенствами. Найдём НОД(299,391)

НОД(299,391)=23

Найдём НОД(23,667)

НОД(23,667)=23

Ответ: НОД (299, 391, 667) = 23

Задание 2. Пользуясь алгоритмом Евклида вычислить НОД и выразить его через исходные числа: (1073; 3683).

Применим алгоритм Евклида к данным числа. Запишем его поэтапно соответствующими равенствами.

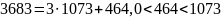
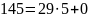
Остаток от деления равен 0, значит НОД равен предыдущему остатку от деления.

Ответ: НОД(1073; 3683)=29

Для нахождения линейного представления этого НОД через исходные числа будем последовательно выражать остатки через исходные числа.

Задание 3. Для пары чисел (1073; 3683).найти наименьшее общее кратное. Результат вычисления НОК проверить разложением чисел на простые множители.

НОК(1073; 3683)=

НОК(1073; 3683)=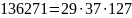

Задание 4. Сократите следующие дроби, представив числитель и знаменатель дроби в каноническом виде: 438875/747843.

Задание 5. Пользуясь расширенным алгоритмом Евклида вычислить НОД и выразить его через исходные числа (899; 493; 9639).

Найдём НОД(899; 493)

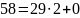
НОД(899; 493)=29

Линейное представление:

(Как найдено? Это тоже повторение вопроса.)

Опишем пошагово линейное представление НОД:

1. Из выражения выразим 29:

Аналогично выразим 58, 87 и 406:

Подставим полученные равенства в выражение и получим линейное представление НОД:

НОД(899; 493; 9639)=НОД(НОД(899; 493);9639)=НОД(29;9639)

Найдём НОД(29;9639)

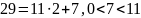
НОД(29;9639)=1

Линейное представление:

Выразим НОД(29; 9639) через исходные числа: