Турищев Л.С. Строительная механика УМК Часть 1. Статически определимые системы, Новополоцк ПГУ 2005

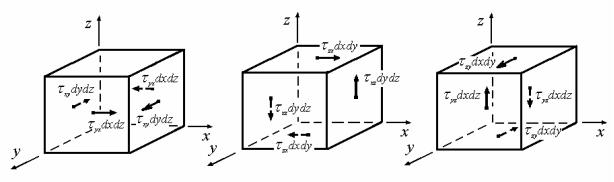
Равнодействующие касательных составляющих внутренних сил с учетом закона парности касательных напряжений

τxy = τyx , τxz = τzx , τyz = τzy

образуют три пары сил

τxy dydz и τyxdxdz,

τxz dydz и τzx dxdy,

τyz dxdz и τzy dxdy,

содинаковыми моментами противоположного направления (рис. 6.15). Следовательно, они являются обобщенными силами с параметрами, равными моментам соответствующих пар сил

Рис. 6.15

Деформация элементарного объема описывается тремя относительными линейными деформациями εx , εy , εz и тремя углами сдвига

γxy , γyz , γzx . Изменения размеров его сторон

εxdx, εy dy, εz dz

являются обобщенными перемещениями для соответствующих обобщенных сил, образованных равнодействующими (6.16). В свою очередь, углы сдвига

γxy , γyz , γzx ,

характеризующие изменение формы элементарного объема, являются обобщенными перемещениями для соответствующих обобщенных сил с параметрами (6.17).

151

С учетом установленных обобщенных сил и обобщенных перемещений, возникающих в окрестности произвольной точки при деформировании тела, получим выражение для действительной элементарной работы внутренних сил

dAв.с. = − 12 [(σx dydz)εx dx +(σy dxdz)εy dy +(σz dxdy)εz dz + +(τxy dydz)dxγxy +(τyz dxdz)dyγyz +(τzxdxdy)dzγzx ]

или

dAв.с. = −12 [σxεx + σyεy + σz εz + τxy γxy + τyz γyz + τzx γzx ]dV , (6.18)

где dV = dxdydz . Аналогично получается и выражение для возможной элементарной работы внутренних сил

dAв′.с. = −[σxεx +σyεy +σzεz + τxyγxy + τyzγyz + τzxγzx ]dxdydz .

Выражение в квадратных скобках, входящее в полученные формулы, дает величину работы на единицу объема упругого тела и называется удельной работой внутренних сил. Тогда полная действительная и возможная работа для всего упругого тела будут, соответственно, равны

V

6.4.2. Работа внутренних сил плоской стержневой конструкции

Рассмотрим произвольную плоскую стержневую конструкцию (рис. 6.16, а), которая образована из прямых стержней и стержней малой кривизны. По статическим свойствам она может быть как статически определимой, так и статически неопределимой. От внешних воздействий (нагрузки, температуры и осадки опор) конструкция в своей плоскости деформируется, и в стержнях возникают внутренние силы.

Поскольку каждый стержень конструкции является упругим телом, рассмотрим элемент произвольного стержня длиной ds (рис. 6.16, б) и выделим в нем элементарный параллелепипед длиной ds и площадью

152

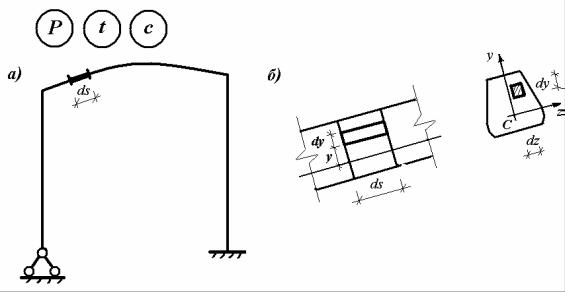
dA = dydz . Будем считать, что поперечное сечение стержня отнесено к главным центральным осям инерции.

Рис. 6.16

В соответствии с гипотезами сопротивления материалов, вводимыми при изучении напряженно-деформированного состояния плоского призматического стержня, и принятой схемой деформирования стержней конструкции будем считать

Тогда внутренние силы, возникающие в конструктивных элементах плоской стержневой системы, будут характеризоваться одним нормальным напряжением

и одним касательным напряжением

Сучетом (6.21) – (6.23) выражения для вычисления действительной

ивозможной элементарной работы внутренних сил плоской стержневой конструкции примут вид

dAв.с. = − 12 [σε+τγ]dAds

и

dAв′.с. = −[σε+ τγ]dAds .

153

Тогда полная действительная и возможная работа для всей плоской стержневой конструкции будут, соответственно, равны

kl A

Вформулах (6.24) и (6.25) суммирование осуществляется по стержням рассматриваемой конструкции.

6.5.Аналитическая форма определения перемещений в плоских стержневых конструкциях от произвольных внешних воздействий

В основе аналитической формы определения перемещений в деформируемых системах лежит принцип возможных перемещений. Согласно этому принципу, если деформируемая система находится в равновесии, то сумма работ всех действующих сил, включая и внутренние силы, на возможных перемещениях системы от положения равновесия равняется нулю.

Возможными перемещениями деформируемой системы называются воображаемые бесконечно малые перемещения, которые допускаются наложенными связями системы. Так как рассматриваемые плоские стержневые конструкции являются линейно-деформируемыми системами, то для них, ввиду линейной зависимости между перемещениями и внешними воздействиями, возможными перемещениями являются любые малые конечные перемещения, которые могут возникать в конструкции.

6.5.1. Выводобщейформулыдляопределенияперемещенийвплоских стержневыхконструкцияхотпроизвольныхвнешнихвоздействий

Пусть имеется некоторая плоская стержневая конструкция, которая подвергается одновременному воздействию нагрузки, температуры и осадке опор (рис. 6.17, а). При задании перемещений опор их нумерация согласуется с нумерацией реакций конструкции.

Как и ранее, принимается, что по статическим свойствам конструкция может быть как статически определимой, так и статически неопределимой. От внешних воздействий конструкция деформируется, и в ней возникают перемещения. Требуется для некоторого сечения K по произвольному направлению i определить его перемещение ∆i .

154

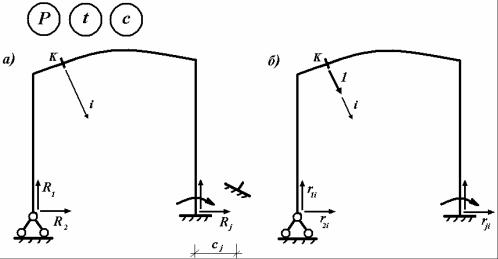
Исходное состояние конструкции назовем действительным состоянием. Будем считать, что для этого состояния известны опорные реакции R1,..., R j и внутренние усилия M , Q, N в стержнях конструкции. Тогда,

как следствие, можно считать известными напряжения σ, τ и деформации ε, γ в любой точке конструкции.

Рис. 6.17

Образуем вспомогательное единичное состояние. Для этого в сечении K заданной конструкции по направлению искомого перемещения приложим безразмерную силу, равную единице (рис. 6.17, б). Также считаем, что во вспомогательном состоянии известны следующие величины:

−единичные опорные реакции r1i ,..., rji ;

−единичные внутренние усилия mi , qi , ni в стержнях конструкции;

−единичные напряжения σi , τi и единичные деформации εi , γi в

произвольной точке конструкции.

Поскольку конструкция во вспомогательном единичном состоянии находится в равновесии, применим к этому состоянию принцип возможных перемещений, задавая в качестве возможных перемещения действительного состояния конструкции. При этом предполагается, что во время придания возможных перемещений температура во всех точках конструкции остается без изменения. Тогда уравнение принципа возможных перемещений будет включать работу единичной силы, единичных опорных реакций, единичных внутренних сил на соответствующих перемещениях действительного состояния и имеет вид

155

В уравнение (6.26) входит единственная неизвестная величина – перемещение ∆i и, следовательно, его решение имеет вид

Формула (6.27) не используется непосредственно для вычисления перемещений в стержневых конструкциях. Но она позволяет выразить искомое перемещение для произвольной плоской стержневой конструкции (статически определимой или неопределимой) при одновременном приложении нагрузки, температурного воздействия и осадки опор через характеристики ее действительного и единичного состояний. Поэтому формула (6.27) имеет фундаментальное значение при определении перемещений в линейно-деформируемых системах и является для них общей формулой.

6.5.2. Упрощения общей формулы при раздельном приложении нагрузки, температурного воздействия и осадки опор

При воздействии на плоскую стержневую конструкцию только нагрузки

ε, γ и напряжения σ, τ, связаны, согласно закону Гука, следующими зависимостями

При этом по-прежнему считаем, что по статическим свойствам рассматриваемая стержневая конструкция может быть как статически определимой, так и статически неопределимой. С учетом (6.28) и (6.29) формула (6.27) примет вид

При упрощении общей формулы для температурного воздействия или осадки опор будем считать плоскую стержневую конструкцию статически определимой системой. В соответствии со свойствами таких конструкций в них не возникают внутренние усилия от этих внешних воздействий.

156

Поэтому при температурном воздействии на статически определимую конструкцию не возникает сдвиговых деформаций

а линейные деформации связаны с изменениями температуры следующей физической зависимостью

Здесь α – коэффициент линейного расширения конструкционного материала и ∆t – приращение температуры в произвольной точке конструкции. Кроме того, как и в случае приложения нагрузки, выполняется условие (6.28).

Подставляя (6.28), (6.31), (6.32) в (6.27), получим следующую формулу для температурных перемещений в статически определимых стержневых конструкциях

Коэффициент линейного расширения α выносить за знак суммы в формуле (6.33) нельзя, так как конструкционный материал стержней конструкции в общем случае может быть разным.

Поскольку при воздействии на статически определимую конструкцию осадки опор в ней не возникают линейные и сдвиговые деформации

ε = 0, γ = 0 ,

то общая формула для определения перемещений в этом случае принимает вид

Полученная формула, в отличие от формул (6.30) и (6.33), является рабочей, так как по ней можно вычислять значения перемещений. При пользовании формулой (6.34) заданные смещения опор c j считаются положи-

тельными, если по направлению они совпадают с соответствующими единичными опорными реакциями rji .

6.5.3. Вывод рабочей формулы для определения перемещений от действия нагрузки

При действии на плоскую стержневую конструкцию произвольной нагрузки нормальные и касательные напряжения, возникающие в ее про-

157

извольной точке, связаны с внутренними усилиями известными из сопротивления материалов формулами

Подставим (6.34) – (6.38) в формулу (6.30) и вычислим внутренний интеграл по площади.

Интеграл для первого слагаемого подынтегрального выражения (6.30) примет вид

После раскрытия скобок и вычисления интеграла в правой части формулы (6.39) получим

При выводе (6.40) следует учесть, что встречающийся при преобразовани-

ях интеграл вида ∫ydA является статическим моментом площади попе-

A

речного сечения и равняется нулю, так как сечение отнесено к главным центральным осям инерции.

Интеграл для второго слагаемого подынтегрального выражения (6.30) примет вид

можно ограничиваться учетом только изгибных деформаций. Это же справедливо для обычных рамных конструкций и только в случае рам повышенной этажности необходим учет продольных деформаций. Совместный учет изгибных и продольных деформаций необходим при определении перемещений в арках и комбинированных системах. А при определении перемещений в ферменных конструкциях достаточно учитывать влияние только продольных деформаций.

6.5.4. Вывод рабочей формулы для определения перемещений от температурного воздействия

Температурное воздействие на стержни конструкции обычно характеризуется двумя независимыми величинами – внутренней температурой tв и наружной температурой tн и зависимой от них величиной – температурой на оси tо . Внутренней температурой всегда считается более высокая температура

tв > tн.

Поэтому внутренняя температура не всегда совпадает с температурой внутри контура конструкции.

Например, если температура внутри контура рамы равняется −25oC , а снаружи – +15oC , то в этом случае tв = +15oC , а tн = −25oC .

Для преобразования формулы (6.33) к виду, позволяющему определять численные значения перемещений от температурного воздействия, выразим приращение температуры в произвольной точке конструкции ∆t через tв и tн .

Поскольку температурные изменения в конструкции происходят с того момента, как завершен монтаж конструкции, то величину ∆t будем определять по отношению к температуре завершения монтажа конструкции. Такая температура называется температурой замыкания tз.

Будем считать, что изменение температуры по высоте поперечного сечения некоторого стержня конструкции происходит по линейному закону (рис. 6.18, а). Такой закон справедлив для основных конструкционных материалов, используемых при возведении строительных сооружений. Как и раньше, считаем, что сечение отнесено к главным центральным осям инерции.

160