
Турищев Л.С. Строительная механика УМК Часть 1. Статически определимые системы, Новополоцк ПГУ 2005
.pdf
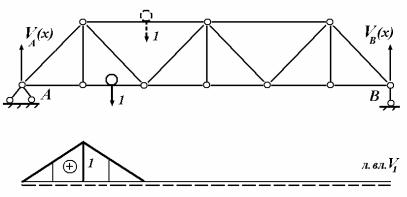
поясу (груз понизу) и по верхнему поясу (груз поверху) (рис. 4.27, а). Предполагается, что движение единичного груза происходит по вспомогательным балочкам, которые опираются на узлы фермы. Таким образом обеспечивается узловое нагружение фермы.
Рис. 4.27
Применение метода рассечения на крупные части к построению линий влияния рассмотрим для продольных сил, возникающих в стержнях O3 и D3 . Рассечем ферму на две части через третью панель верхнего и четвертую панель нижнего поясов (рис. 4.27, б). При нахождении продольных сил O3 и D3 как некоторых функций от абсциссы x произвольного положения единичного груза будем рассматривать три его положения – слева и справа от рассеченной панели и в пределах этой панели.
Линия влияния O3 . Рассмотрим первое произвольное положение единичного груза – груз понизу и слева от рассеченной панели (4.27, б). Для определения продольной силы O3 рассмотрим равновесие правой отсеченной части фермы и составим уравнение моментов относительно моментной точки этого усилия RO3
∑M Rпр.ч. = 0; - O3 (x) h −VB (x) 2a = 0 , |
|
|||||
O |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
откуда |
2a |
|
|
|
|
|
O (x) = − |
V |
B |
(x) . |
(4.5) |
||
|
||||||
3 |
h |
|
|
|||
101 |
|
|
|
|
||
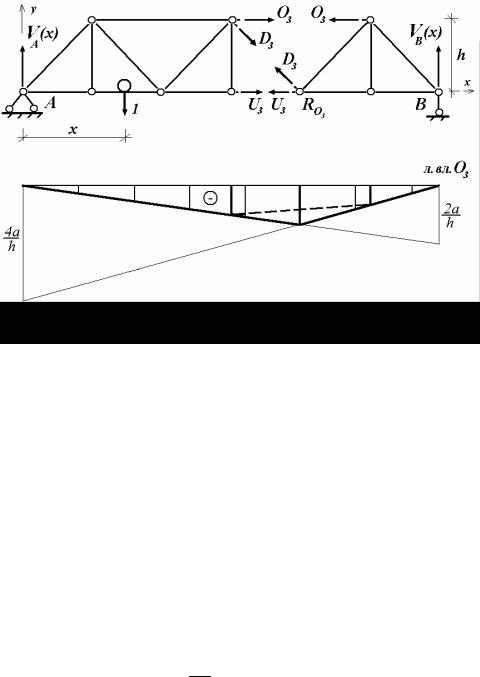
Из (4.5) следует, что левый участок линии влияния O3 имеет очертание линии влияния правой опорной реакции фермы VB (x) , ординаты которой
должны быть умножены на величину − 2ha (рис. 4.28).
Рис. 4.28
Рассмотрим второе произвольное положение единичного груза – груз понизу и справа от рассеченной панели. Для определения продольной силы O3 рассмотрим равновесие левой отсеченной части фермы и составим
уравнение моментов относительно моментной точки этого усилия
∑M Rл.ч. |
= 0; O3 (x) h −VA (x) 4a = 0 , |
|
||||
O |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
откуда |
|
|
|
|
|
|
|
O (x) = − |
4a |
V |
A |
(x) . |
(4.6) |
|
|
|||||
|
3 |
h |
|
|
||
Из (4.6) следует, что правый участок линии влияния O3 |
имеет очертание |
|||||
линии влияния левой опорной реакции фермы, ординаты которой должны быть умножены на величину − 4ha (рис. 4.28).
Рассмотрим третье произвольное положение единичного груза – груз понизу и в пределах рассеченной панели. Так как изменение продольной силы O3 будет описываться некоторой линейной функцией от абсциссы x
единичного груза, а концевые значения ординат этой функции могут быть найдены из (4.5) и (4.6), то этого достаточно для получения очертания соединительного участка линии влияния.
102
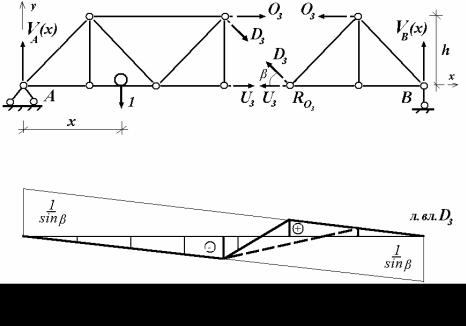
Очертание линии влияния продольной силы O3 при движении груза
понизу показано на рис. 4.28 сплошной линией. Левый и правый участки линии влияния пересекаются под моментной точкой RO3 .
Поскольку при движении единичного груза поверху при составлении уравнений равновесия для трех рассмотренных произвольных положений единичного груза ничего не изменяется, то полученные соотношения (4.5) и (4.6) справедливы для такого движения груза. Однако при этом изменяются границы рассеченной третьей панели верхнего пояса по сравнению с аналогичной панелью нижнего пояса. Поэтому на линии влияния O3 изме-
нится очертание соединительного участка, который показан на рис. 4.28 пунктирной линией.
Линия влияния D3 . Для определения продольной силы D3 при поло-
жении единичного груза понизу и слева от рассеченной панели (рис. 4.27, б) составимсуммупроекцийсилправойотсеченной частифермынаосьy
∑yпр.ч. = 0; D3 (x) sin β+VB (x) = 0 , |
|
||||||
откуда |
|
1 |
|
|
|
|
|
D |
(x) = − |
V |
B |
(x) . |
(4.7) |
||
sin β |
|||||||
3 |
|
|
|
|
|||
Из (4.7) следует, что левый участок линии влияния D3 имеет очертание линии влияния правой опорной реакции фермы, ординаты которой умно-
жены на величину − sin1 β (рис. 4.29).
Рис. 4.29
103
Для определения продольной силы D3 при положении единичного груза понизу и справа от рассеченной панели составим сумму проекций сил левой отсеченной части фермы на ось y
∑y л.ч. = 0; |
- D3 (x) sin β+VA (x) = 0 , |
|
|||||
откуда |
|
|
|
|
|
|
|
D |
(x) = |
1 |
V |
A |
(x) . |
(4.8) |
|
sin β |
|||||||
3 |
|
|
|
|
|||
Из (4.8) следует, что правый участок линии влияния D3 имеет очертание линии влияния левой опорной реакции фермы, ординаты которой умноже-
ны на величину sin1 β (см. рис. 4.29).
Для получения соединительного участка, как и в предыдущем случае построения линии влияния, используются концевые значения D3 , полученные из (4.7) и (4.8). Очертание линии влияния D3 при движении груза понизу показано на рис. 4.29 сплошной линией. Очертание соединительного участка, соответствующее движению единичного груза поверху, показано на рис. 4.29 пунктирной линией.
4.4.2. Применение для построения линий влияния метода вырезания узлов
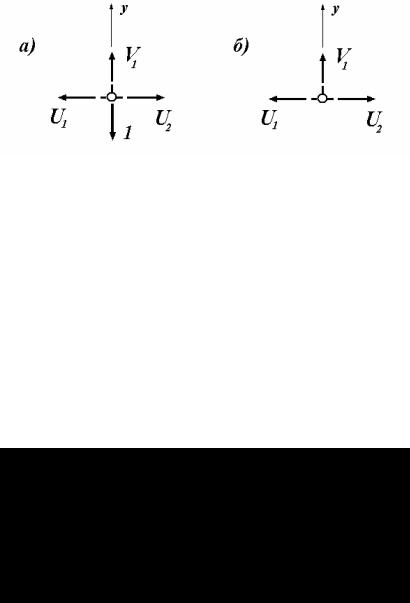
Будем по-прежнему рассматривать ферму, показанную на рис. 4.27, а. Применим метод вырезания узлов для построения линии влияния продольной силы, возникающей в дополнительной стойке V3 . Вырежем узел нижнего пояса фермы, к которому примыкает эта стойка (рис. 4.30). При нахождении продольной силы V3 будем рассматривать три положения движущегося единичного груза по отношению к вырезанному узлу – груз в узле, груз вне узла и вне рассеченных панелей, груз в рассеченных панелях.
Рис. 4.30
104
Рассмотрим первое положение единичного груза – груз понизу и в узле (рис. 4.30, а). Для определения продольной силы V3 рассмотрим равновесие узла и составим сумму проекций сил, приложенных к узлу, на ось y
∑y = 0; V3 −1 = 0 ,
откуда
V3 =1. |
(4.9) |
Соотношение (4.9) дает значение одной ординаты линии влияния V3 , соответствующей расположению единичного груза в узле.
Рассмотрим второе положение единичного груза – груз понизу и вне узла и вне рассеченных панелей (рис. 4.30, б). Для определения продольной силы V3 также составим сумму проекций узловых сил на ось y
∑y = 0; V3 (x) = 0 ,
откуда
V3 (x) = 0 . |
(4.10) |
Из соотношения (4.10) следует, что очертание линии влияния V3 при втором положении единичного груза совмещается с осью x. Такой результат очевиден, так как имеем трехстержневой ненагруженный узел, в котором оси двух стержней нижнего пояса направлены по одной прямой. Следовательно, дополнительная стойка V3 является нулевой при движении единичного груза вне рассеченных панелей, полученных при вырезании узла.
Для получения двух соединительных участков используются концевые значения V3 , найденные из (4.9) и (4.10). Очертание линии влияния V3 показано на рис. 4.31.
Рис. 4.31
105
Поскольку при движении единичного груза поверху по отношению к вырезанному узлу он может занимать только положение вне узла и вне рассеченных панелей, то продольная сила V3 при любом его положении
описывается соотношением V3 (x) = 0 и очертание линии влияния совмещается с осью x. На рис. 4.31 оно показано пунктирной линией.
4.5.Анализ распределения продольных сил
встержнях простых ферм
Впростых фермах при узловой нагрузке можно без численного определения продольных сил, возникающих в элементах поясов и решеток, устанавливать знаки этих сил и закономерности в изменениях их величин. Умение выполнять такой анализ позволит качественно предвидеть результаты расчетов ферм и, следовательно, осуществлять контроль их правильности.
4.5.1.Анализ знаков усилий в поясах ферм
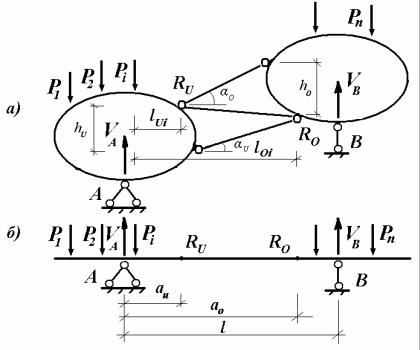
Изобразим произвольную простую ферму в виде двух дисков, соединенных стержневым участком, включающим элемент верхнего пояса O , элемент нижнего пояса U и раскос D (рис. 4.32, а). Будем считать, что к ферме приложена некоторая узловая нагрузка. Одновременно рассмотрим балку (рис. 4.32, б), имеющую одинаковые с фермой пролет, схему нагружения и, следовательно, опорные реакции.
Рис. 4.32
106
Рассечем ферму на две части и составим уравнения моментов, например, для левой части, относительно моментных точек усилий элементов поясов O и U
∑M RлO.ч. = 0; OhO cos αO + M RбалO = 0;
∑M Rл.Uч. = 0; UhU cos αU + M RбалU = 0;
|
л.ч. |
|
л.ч. |
где M Rбал =VAaO − ∑PilOi |
и M Rбал =VAaU − ∑PilUi – изгибающие моменты в |
||
O |
i |
U |
i |
|
|
||
сечениях балки под соответствующими моментными точками (рис. 4.33). Тогда выражения для внутренних усилий O и U принимают вид
M Rбал |
|
|
O |
|
|
O = − h cos αO |
(4.11) |
|
M Rбал |
. |
|
|
|
|
U = U h cos αU
Рис. 4.33
Из (4.11) следует, что знаки продольных сил, возникающих в поясах простых ферм, следующим образом зависят от знаков балочных изгибающих моментов под моментными точками этих усилий
M Rбал > 0; O < 0 и U > 0;
M Rбал < 0; O > 0 и U < 0 .
Следовательно, при положительных балочных моментах соответствующие элементы верхнего пояса сжаты, а нижнего – растянуты. При отрицатель-
107

ных балочных моментах картина распределения знаков усилий в поясах обратная. Важно подчеркнуть, что очертание решетки фермы не влияет на картину распределения знаков усилий в поясах.
Поскольку для анализа знаков продольных сил в поясах ферм величины балочных моментов не требуются, то для его проведения достаточно иметь только качественное очертание эпюр балочных моментов. Получение такого очертания балочных эпюр не представляет особой сложности. Поэтому с помощью соотношений (4.11) можно достаточно просто для заданной схемы нагружения фермы без вычислений проанализировать, какие элементы поясов будут растянуты, а какие – сжаты.
4.5.2. Анализ распределения величин усилий в поясах ферм
Для установления качественной картины изменения величин усилий в поясах фермы по длине пролета будем в пределах каждой панели пренебрегать разницей высот и различием в положениях моментных точек. Второе позволяет отказаться от необходимости рассмотрения конкретного очертания решетки. Кроме того, будем считать угол наклона элементов поясов постоянным в пределах половины пролета. Последнее условие не справедливо только для ферм с полигональным очертанием поясов.
С учетом введенных предположений соотношения (4.11) принимают
вид
O,U = m |
M бал |
C , |
(4.12) |
|
h |
||||
|
|
|
где C – константа. Из (4.12) следует, что величина усилий в поясах характеризуется величиной дроби
M бал
.
h
Качественно величина дроби описывается разностью отрезков, изображающих графически величины, стоящие в знаменателе и числителе.
Поскольку изменение числителя дроби графически описывается очертанием эпюры балочных изгибающих моментов, а знаменателя – очертанием внешнего контура фермы, то изменение величин продольных сил в поясах будет описываться фигурой, заключенной между внешним контуром фермы и эпюрой балочных изгибающих моментов. Чем больше разность соответствующих ординат, тем меньше величины продольных сил, и наоборот.
108
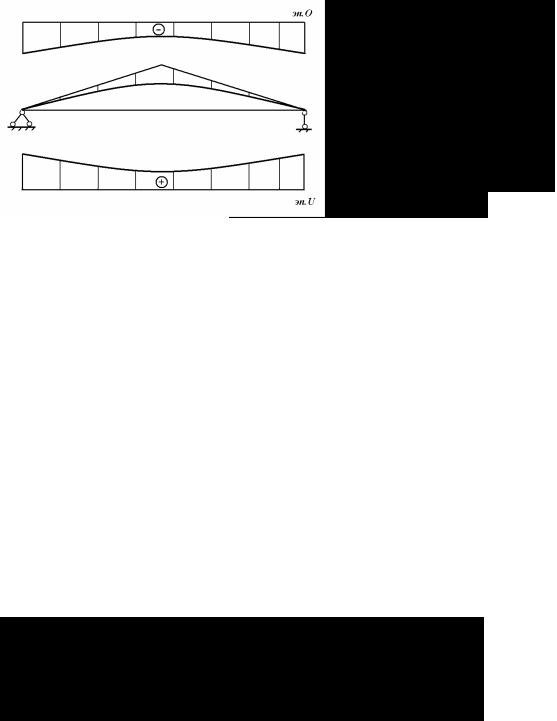
Покажем применение рас- |
Эп. О |
смотренного подхода к анализу |
|
распределения величин усилий в |
|
поясах фермы, внешний контур |
|
которой имеет треугольное очер- |
|
тание. Нагрузку считаем близкой к равномерной и поэтому балочная эпюра моментов будет иметь очертание квадратной параболы. Вписывая эпюру балочных моментов в контур фермы, получим,
что величины усилий в поясах уменьшаются по модулю от опор к средине пролета фермы (рис. 4.34). Фактическое изменение усилий в поясах будет не непрерывным, а ступенчатым, так как величины балочных моментов должны браться только под соответствующими моментными точками.
4.5.3. Анализ знаков усилий в раскосах и основных стойках ферм
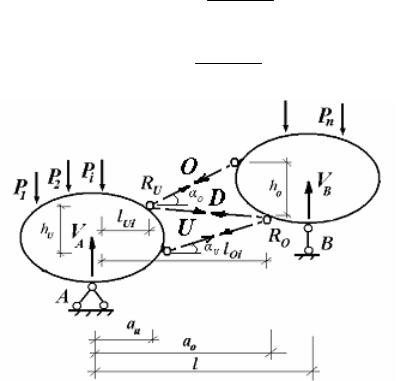
Знаки усилий в раскосах и основных стойках произвольной простой фермы связаны с закономерностями изменения величин усилий в поясах этой фермы. Рассмотрим некоторую ферму с треугольной решеткой и узловой схемой нагружения одного из ее поясов. Считая поочередно нагруженными верхний и нижний пояс, вырежем по одному узлу, соответственно, из ненагруженного нижнего пояса (рис. 4.35, а) и ненагруженного верхнего пояса (рис. 4.35, б). На рис. 4.35 раскосы приняты растянутыми, восходящие раскосы обозначены Dв , а нисходящие – Dн.
Рис. 4.35
При рассмотрении равновесия вырезанных узлов сначала будем считать, что величины усилий в поясах увеличиваются к средине пролета фермы. Следовательно, для рассматриваемых узлов усилия в элементах поясов получают некоторые приращения ∆U > 0 и ∆O > 0 . Тогда из силовых
109
вых треугольников этих узлов следует, что нисходящие раскосы растянуты, а восходящие раскосы сжаты (рис. 4.36).
Рис. 4.36
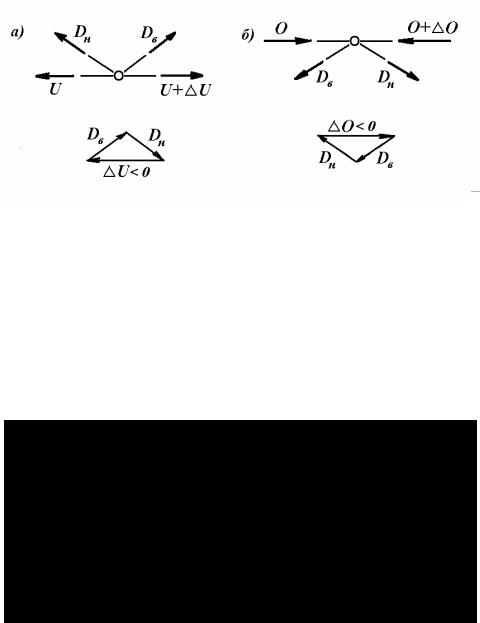
Если при рассмотрении равновесия вырезанных узлов принять, что величины усилий в поясах уменьшаются к средине пролета фермы, то приращения усилий в элементах поясов должны удовлетворять условиям ∆U < 0 и ∆O < 0 . В этом случае из силовых треугольников рассматриваемых узлов следует, что нисходящие раскосы сжаты, а восходящие раскосы растянуты (рис. 4.37).
Рис. 4.37
Поскольку основные стойки можно рассматривать как частные случаи раскосов с углом наклона 90°, то все сформулированные критерии распространяются и на них.
Так, например, для треугольной фермы с раскосной решеткой (рис. 4.38) основные стойки играют роль восходящих раскосов.
110
