6.3.2 Определение экономически целесообразных диаметра трубопровода и скорости потока

В простом трубопроводе в виду постоянства его диаметра движение среды во всех его сечениях одинаково. Попробуем определить величину этой скорости, которая должна быть найвыгоднейшей с экономической точки зрения.

Положим, что имеем водопроводную сеть, выполненную из труб определенного диаметра. Представим теперь, что диаметр труб данной сети начинаем уменьшать. В результате этого получаем следующее: скорость движения воды по сети возрастает ( ); потери напора в этих трубах будут растут ( ); а следовательно будет расти и мощность насосов, перекачивающих воду ( ). Т.е. можно утверждать, что эксплуатационные затраты Э при этом возрастают.

Также бесспорно выглядит и тот факт, что уменьшение диаметра труб магистрали снижает стоимость самой магистрали, т.е. величину капитальных затрат З_К на ее сооружение. Приводя капитальные затраты (с учетом срока окупаемости) и эксплуатационные затраты к единице перемещаемой среды строят графики зависимости K_пр=f(d) и Э_пр=f(d) (см. рисунок 6.3). Тогда суммарные затраты З_пр выразятся кривой полученной как сумма З_пр=Э_пр+К_пр=f(d). Абсцисса d_э определяет область экономически выгодного диаметра, а следовательно и диаметра, при котором приведенные затраты будут минимальными т.е. К_mо min.

По В.С. Яблонскому, приближенно можно принять, что экономически наивыгоднейший диаметр обычно соответствует скорости примерно 1 м/с, т.е. диаметру, определяемому по формуле:

(6.23)

где секундный расход жидкости, м³/с.

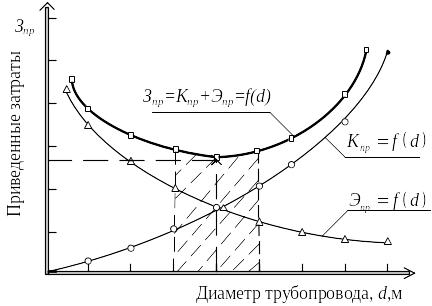
о – график зависимости приведенных капитальных затрат K_пр=f(d);

D – график зависимости приведенных эксплуатационных затрат Э_пр=f(d);

– результирующий график приведенных затрат З_пр=К_пр+Э_пр=f(d)

Рисунок 6.3 – К определению экономически выгодного диаметра

Проведенные расчеты показали, что для определенного диаметра трубы есть своя экономичная скорость. Величина этой скорости для перемещения маловязких жидкостей в напорном трубопроводе лежит в пределах 1 ÷3 м/с. Ниже, в таблице 6.2, приведены экономичные скорости движения жидкости в трубах определенного диаметра.

Таблица 6.2. – Экономичные скорости движения жидкости в трубах различного диаметра

Размер условного прохода, Dy, м	0,10	0,20	0,25	0,30
Экономичная скорость, u, м/с	0,75	0,90	1,10	1,25

6.3.3 Построение напорной характеристики простого трубопровода

При гидравлическом расчете трубопровода весьма широко используются графические методы расчета, основанные на понятии напорной характеристики трубопровода. Применение графических методов значительно упрощает расчет, а в отдельных случаях является единственно возможным приемом, позволяющим получить решение. Прежде всего покажем, что для любого трубопровода и в частности для простого существует зависимость его гидравлического сопротивления (потерь напора) от пропускной способности V_c (производительности).

В уравнение гидравлических потерь (6.21) подставим среднюю скорость потока, выраженную из уравнения объемного секундного расхода с учетом площади его поперечного сечения в предположении что труба имеет круглое сечение:

V_c=su; ; откуда , (6.24)

Тогда:

Н_п= , (6.25)

т. е.

H_п= , (6.26)

Зависимость H_п= представляет собой напорную характеристику. Как не трудно убедиться она представляет собой степенной одночлен. Показатель степени “m” и коэффициент пропорциональности k может быть определен с учетом режимов движения жидкости.

Для ламинарного режима движения коэффициент гидравлического трения , а с учетом расхода жидкости и того, что трубопровод выполнен из труб круглого сечения,

(6.27)

Подстановка значения l в уравнение (6.25) дает выражение для величины потребного напора при ламинарном режиме движения:

(6.28)

Из уравнения (6.28) следует, что графическая характеристика трубопровода при ламинарном режиме движения представляет прямую линию. , причем , а показатель степени в уравнении (6.28) m=1,0.

_Для развитого турбулентного режима движения, когда Re>10⁴ _{коэффициент гидравлического трения определяется по уравнению}

_{Б.Л. Шефринсона:}

Подстановка значения l в уравнение (6.25) приводит к зависимости:

, (6.29)

т. е.

, (6.30)

которая, представляет собой уравнение параболы, т.к. m=2,0 а коэффициент пропорциональности .

На нижеприведенном рисунке 6.4 представлены графические характеристики трубопровода, схема которого приведена на рисунке 6.2 для различных режимов движения подвижных сред.

Для переходного режима движения когда показатель степени в уравнении (6.26) m =1,75

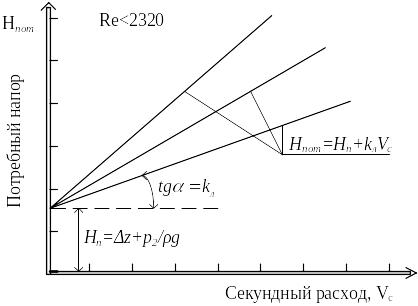
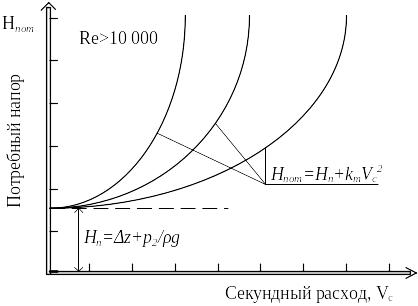
а) б)

Рисунок 6.4 – Графические характеристики трубопровода при ламинарном (а) и турбулентном (б) режимах течения жидкости