Тема 6 гидравлические потери

6.1 Гидравлические потери по длине трубопровода.

6.2 Гидравлические потери на преодоление местных сопротивлений

6.3 Гидравлический расчет простого трубопровода.

6.3.1 Расчет диаметра трубопровода

6.3.2 Определение экономически целесообразных диаметра трубопровода и скорости потока

6.3.3 Построение напорной характеристики простого трубопровода

6.4 Примеры гидравлических расчетов

6.5 Контрольные задания

Движение реальной жидкости по трубам и каналам всегда сопровождается потерями удельной энергии потока, т.е.потерями напора. При этом энергия потока тратится как на преодоление сил трения 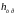так и на преодоление местных сопротивлений 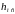. Таким образом общие энерго потери в потоке складываются из двух составляющих:

(6.1)

Определение величины потерь напора (гидравлических потерь) является одним из основных вопросов всех гидравлических расчетов т.к. их знание позволяет обоснованно подходить к выбору насосного и вентиляторного оборудования.

6.1 Гидравлические потери по длине трубопровода.

Для всех случаев движения подвижных сред в трубах и каналах величина потерь напора на преодоление сил трения определяется по уравнению Дарси – Вейсбаха:

(6.2)

гдеλ–коэффициент гидравлического трения (коэффициент Дарси);

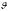– средняя скорость движения среды, м/с;

d_э – эквивалентный диаметр трубопровода, м;

l–длинатрубопровода,м.

Эквивалентный диаметр трубопровода или канала определяется по гидравлическому радиусу потока, определяемому по уравнению (4.1) как отношение площади живого сечения потокаSк его смоченному периметру χ т.е. .

При определении коэффициента гидравлического трения λ используются графики И. Никурадзе (см. рисунок 6.1) либо расчетные зависимости. При этом весь диапазон режимов движения потоков разбит на четыре зоны которые характеризуются одинаковым характером поведения графика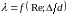 , а следовательно описываются одними и теми же уравнениями.

Рисунок 6.1– График зависимости коэффициента гидравлического трения λ от режима движения среды в трубопроводе и относительной шероховатости стенок трубы ε (графики И.Никурадзе).

В свою очередь режим движения потока определяется по значению критерия Рейнольдса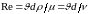 . На графиках И.Никурадзе и в расчетных зависимостях отношение абсолютной шероховатости стенок трубы Δ к диаметру трубы d заменяют относительной шероховатостью стенки 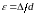. Величина абсолютной шероховатости стенки трубы определяется по таблицам в зависимости от материала стенки.

Для наглядности расчет коэффициента гидравлического трения и потерь напора по длине трубопровода представлен блок – схемой на рисунке 6.2

Весь диапазон изменения режимов движения разбивается на четыре области гидравлического трения. Так первая область – область ламинарного режима ограничивается значениями Re<2320 ( lnRe<3.36 ). Здесь все опытные точки, независимо от шероховатости стенок трубопровода укладываются на одну прямую линию, уравнение которой

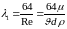(6.3)

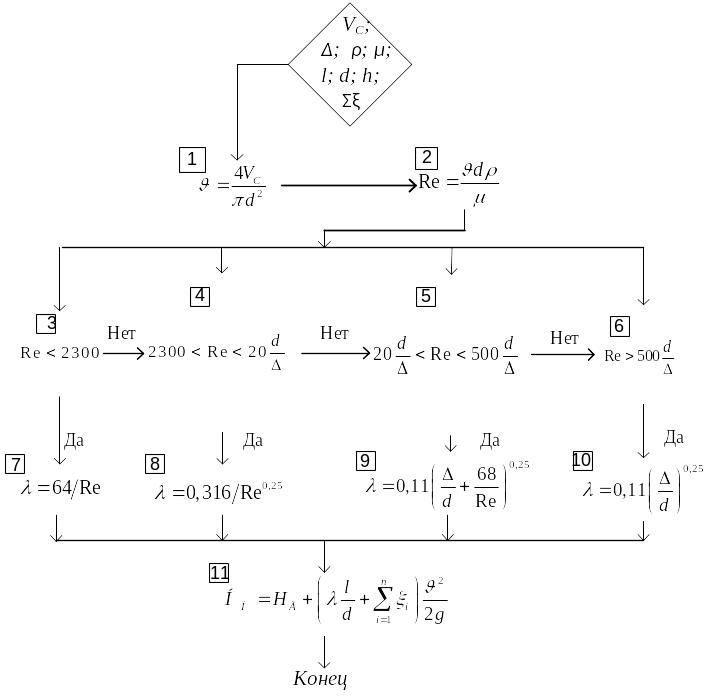
Рисунок 6.2 – Блок-схема расчета коэффициента гидравлического трения и потерь напора по длине трубопровода

Вторая область, расположенная между значениями критерия Рейнольдса Re≈2320 и Re≈4000 область неустойчивого режима или переходная. Здесь возможно существование как ламинарного, так и турбулентного режимов, экспериментальные точки имеют значительный разброс. Поэтому ее протяженность продлевается до области гидравлически шероховатых труб и захватывает область гидравлически гладких. Эта область ограничена значениями критерия Рейнольдса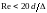 . Здесь толщина вязкого подслоя δ_л существенно больше высоты выступов шероховатости Δ и турбулентное ядро потока не соприкасается с ним. Значение коэффициента гидравлического трения рассчитывается по уравнению Блаузиуса:

(6.4)

Третья область– область гидравлически шероховатых труб или зона доквадратичного закона сопротивления. В этой области λ=f(Re, ε) т.к. толщина вязкого подслоя δ_л становится соизмеримой с высотой неровностей. При этом поток начинает взаимодействовать с выступающими неровностями стенки, в результате этого в потоке возникают дополнительные вихри и соответственно возрастают потери энергии потоком

Область «гидравлически шероховатых» труб лежит в пределах 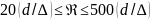. Для расчета коэффициента трения в этой зоне рекомендуется уравнение А.Д.Альтшуля:

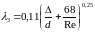(6.5)

Четвертая область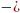 зона «квадратичного закона сопротивления». Здесь коэффициент λ не зависит от критерия Рейнольдса. Коэффициент λ, а следовательно и h_тр зависят только от относительной шероховатости т.е. λ=f(ε). Эта зона начинается при значениях 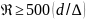. При высоких значенияхRe отношение 68/Reстремится к нулю, а поэтому из уравнения (6.5) опускается и уравнение Альтшуля преобразовано В.Л. Шефринсоном к виду (6.6) и носит его имя.

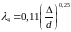(6.6)

Для труб некруглого сечения в формулах (6.3–6.6) вместо диаметра d подставляется значение эквивалентного диаметра.

При ламинарном движении жидкости в круглых трубах потери напора и давления можно также определить по формуле Пуазейля:

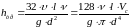, (6.7)

,

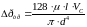где ν – кинематическая вязкость, м²/с;

– средняя скорость потока, м/с;

V_c – расход жидкости, м³/с;

l,d – длина и диаметр трубы, м.

Коэффициент трения λ_н при неизотермическом движении потока выражается через общий коэффициент λ. Для его расчета используются значения ρ и μ среды взятые при средней ее температуре на данном участке.

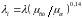(6.8)

где μ_ст и μ_ж коэффициент динамической вязкости жидкости при температуре стенки и средней температуре жидкости соответственно.

При неизотермическом движении газа можно пользоваться приближенной формулой Кутателадзе

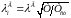(6.9)

гдеТ и Т_ст средняя температура газа и стенки.