3.4. Законы пропорциональности для центробежных машин

Согласно теории подобия физических процессов, подобными считаются те устройства и процессы для которых соблюдается подобие геометрическое, кинематическое, подобие начальных и граничных условий. Применительно к центробежным нагнетателям для подобия нагнетателей необходимо соблюсти геометрическое, кинематическое и динамическое их подобие.

Геометрическое подобие насосов предполагает пропорциональность всех сходственных размеров их проточной части (d; D; b), равенство углов определяющих форму лопаток ( ), а также одинаковое их число (z).

Геометрически подобные насосы обладают численно равными соотношениями (линейный масштаб подобия) сходственных размеров, т.е. для них соблюдается соотношение:

(3.21)

где − линейный масштаб подобия.

Кинематическое подобие предполагает, что отношение скоростей модели и натурного образца 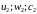в сходственных точках должно сохраняться постоянным

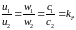(3.22)

Однако для переносного движения соотношение скоростей

(3.23)

Соотношения скоростей относительного движения определим, используя уравнение расхода (3.12)

(3.24)

Вместе с тем из соотношений (3.22) и (3.24) следует, что 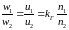подставим полученное выражение в уравнение (3.24) и выразим соотношение производительностей для подобных насосов:

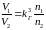(3.25)

Отсюда следует вывод: подачи геометрически подобных насосов, работающих на подобных режимах, относятся друг к другу как числа оборотов, умноженные на куб линейного масштаба подобия.

Динамическое подобие предполагает, подобие процессов передачи энергии от рабочего колеса к потоку жидкости.

(3.26)

т.е. напор, развиваемый подобными насосами в подобных режимах, пропорционален линейному масштабу подобия в квадрате и соотношению частот вращения во второй степени.

Из выражения для затрат мощности, потребляемой насосами (1.1), следует что:

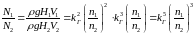(3.27)

т.е. мощность насоса пропорциональна линейному масштабу размеров в пятой степени, соотношению частот вращения рабочих колес насосав в третьей степени и соотношению плотностей перекачиваемых жидкостей.

Если рассмотреть подобные режимы работы одного и того же насоса 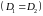при разных частотах вращения рабочего колеса и 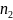, то уравнения (3.25) (3.26) и (3.27) упрощаются до вида:

(3.28)

Этими формулами пользуются для пересчета рабочих параметров насоса с одной частоты вращения рабочего колеса на другую, и они называются законами пропорциональности для центробежных машин.