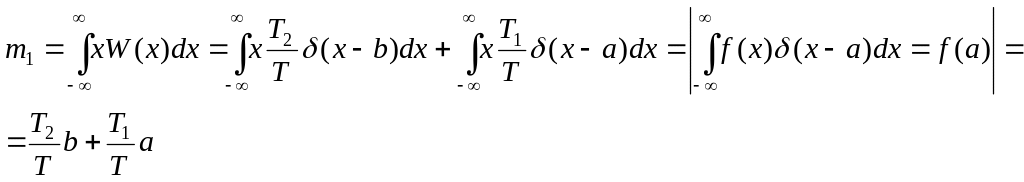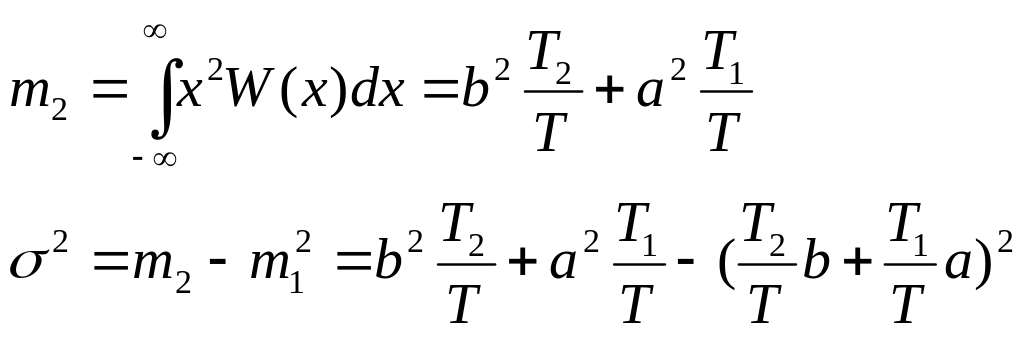- •2.Разложение сигналов в ряд по ортогональным функциям …………10
- •7.2. Амплитудный модулятор. ……………………………………...32
- •7.3.Статическая модуляционная характеристика(смх)…………..33
- •7.4. Энергетические показатели ам. ………………………………36
- •Инструкция по использованию студентами информационной базы учебной дисциплины "Теория электрической связи"(ч.1)
- •Методика итогового компьютерного контроля
- •Предисловие
- •1.Обобщённая структурная схема системы связи. Система связи - это совокупность технических устройств, которые позволяют передать сообщение от источника к получателю.
- •Источник информации – источник сообщения подлежащего передаче (человек, окружающая среда и т.П.). Сообщение - речь, музыка, текст, изображение, параметры некоторых объектов и т.П.
- •Какие блоки входят в состав приемника?
- •2.Разложение сигналов в ряд по ортогональным функциям.
- •2.1. Общие положения
- •2.2. Ряд Фурье.
- •3.Теорема Котельникова.
- •3.1.Разложение непрерывных сигналов в ряд Котельникова
- •Спектр периодической последовательности - импульсов в соответствии с формулой для u(t) имеет следующий вид :
- •3.2. Спектр дискретизированного сигнала.
- •3.3. Спектр дискретизированного сигнала при дискретизации импульсами конечной длительности (сигнал амплитудно-импульсной модуляции или аим сигнал).
- •3.4. Восстановление непрерывного сигнала из отсчётов.
- •3.5. Погрешности дискретизации и восстановления
- •4.Классификация электрических цепей.
- •5. Аппроксимация характеристик.
- •5.1.Общие положения
- •5.2. Аппроксимация полиномом.
- •5.3. Линейно-ломаная аппроксимация.
- •6. Методы расчёта спектра тока на выходе нэц.
- •6.1. Метод угла отсечки.
- •6.2. Расчёт амплитуд гармоник методом
- •6.3. Расчёт амплитуд гармоник методом 3-х и 5-и ординат.
- •7.Амплитудная модуляция (ам).
- •7.1.Временная и спектральная диаграммы сигнала ам
- •В ременная диаграмма модулированного сигнала ам:
- •7.2. Амплитудный модулятор.
- •Резонансный контур настроен на и выделяет частоты . Сопротивление резонансного контура имеет вид:
- •7.3.Статическая модуляционная характеристика
- •7.4. Энергетические показатели ам.
- •7.5. Балансная ам (бам)
- •7.6.Однополосная модуляция (ом)
- •Детектирование (демодуляция) сигналов ам.
- •8.1.Диодный детектор сигналов ам
- •8.2.Квадратичный детектор.
- •8.3. Линейный детектор.
- •8.4.Статическая характеристика детектора
- •9.Частотная модуляция (чм).
- •9.1.Временная и спектральная диаграммы сигнала чм
- •9.2. Формирование чм сигнала.
- •9.3.Статическая модуляционная характеристика (смх).
- •Выбор рабочего режима по смх.
- •9.4. Детектирование сигналов чм.
- •Расчет рабочего режима по схд.
- •10.Фазовая модуляция (фм).
- •10.1.Сравнение фм и чм
- •10.2.Фазовый (синхронный ) детектор (фд).
- •11. Случайные процессы.
- •11.1.Характеристики случайных процессов
- •Функция распределения вероятностей сп (фрв).
- •Двумерная фрв.
- •Функция плотности вероятностей случайного процесса ( фпв)
- •Числовые характеристики случайного процесса .
- •Стационарность.
- •Эргодичность.
- •11.2.Нормальный случайный процесс( гауссов процесс).
- •11.3.Фпв и фрв для гармонического колебания со случайной начальной фазой.
- •11.4.Фпв для суммы нормального случайного процесса и гармонического колебания со случайной начальной фазой.
- •11.5.Огибающая и фаза узкополосного случайного процесса.
- •11.6.Фпв и фрв для дискретных случайных процессов.
- •11.7.Нелинейные безынерционные преобразования случайного процесса.
- •11.8.Фпв процесса на выходе идеализированного ограничителя.
- •11.9.Фпв процесса на выходе идеального ограничителя.
- •11.10.Линейные (инерционные) преобразования случайного процесса. Линейная инерционная система – это линейный фильтр.
- •12.Функция корреляции.
- •13.Энергетический спектр.
- •14.Соотношение Винера - Хинчина и его применение к решению задач
- •15. Модели непрерывных каналов связи.
- •16. Введение в теорию цифровой фильтрации
- •Заключение
11.4.Фпв для суммы нормального случайного процесса и гармонического колебания со случайной начальной фазой.
Рассмотрим случайный процесс z(t), равный:
Z(t) = x(t) + Asin (wt+ )
где x(t) - нормальный случайный процесс;
Asin (wt+ ) - гармоническое колебание со случайной начальной фазой.
W(z) в этом случае находится сверткой.
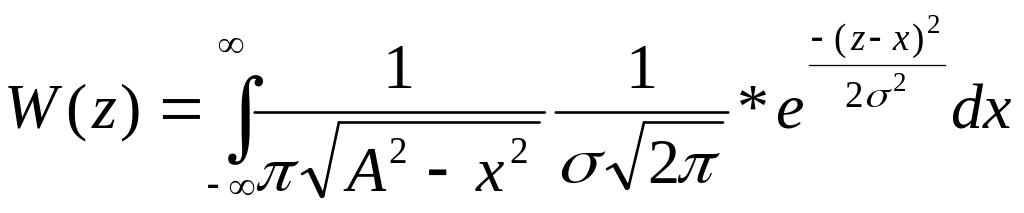
Вид ФПВ, т.е. W(z) зависит от параметра:
![]()
W(z)
h2=0 h2=
 h2=
6
h2=
6
Рис.10.8.
 0
z
0
z
h2 = 0 - нормальный случайный процесс (чистый шум).
h2 - одно гармоническое колебание.
11.5.Огибающая и фаза узкополосного случайного процесса.
Случайный процесс y(t) = Um(t) cos ( 0t+(t) ) называется узкополосным, если его ширина спектра значительно меньше, чем средняя частота 0.
Um(t) - огибающая случайного процесса (случайная амплитуда) на рис.11.9;
(t) - фаза случайного процесса.
Для нормального случайного процесса фаза (t) распределена равномерно (см. выше).

 u(t)
Um(t)
u(t)
Um(t)
Рис.11.9.
t

Огибающая нормального случайного процесса Um(t) распределена по закону Релея:
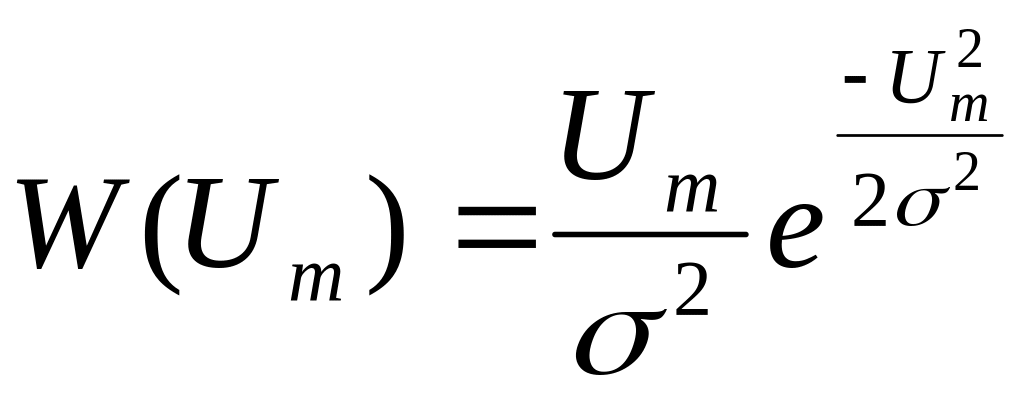 ;
Um
0
;
Um
0
W(Um)
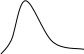

 з-н
Релея
з-н
Релея
з-н Райса Рис.11.10.
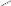
0 Um
Если узкополосный случайный процесс есть сумма нормального шума и гармонического колебания с амплитудой А, то его огибающая распределена по обобщенному закону Релея (закон Райса):
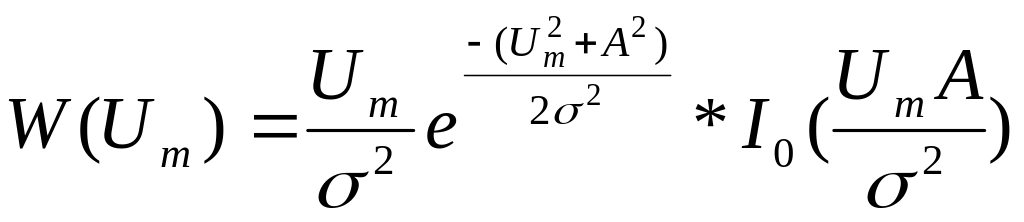 закон
Райса.
закон
Райса.
I0(.) - функция Бесселя от мнимого аргумента.
11.6.Фпв и фрв для дискретных случайных процессов.
Дискретные случайные процессы принимают с определенной вероятностью значения, отличающиеся одно от другого на конечную величину. Вероятность таких значений – число не равное 0.
Рассмотрим реализацию дискретного случайного процесса.
x(t)
а
T1

Т 2 t Рис.11.11
 b
b
T1+T2=T
Для эргодического стационарного случайного процесса усреднение по множеству реализаций эквивалентно усреднению по времени одной реализации.
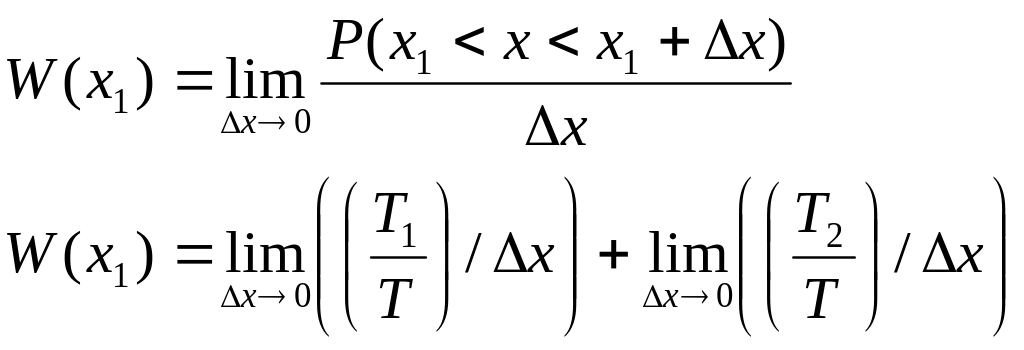
T1/T - вероятность того, что случайный процесс принимает
значение а.
T2/T - вероятность того, что случайный процесс принимает
значение b.
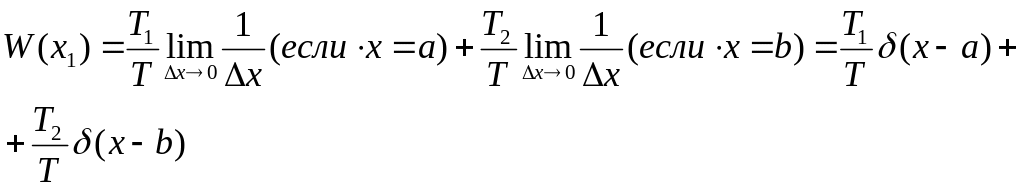
Ф![]() ПВ
заданного
случайного процесса в соответствии с
полученным выражением показана на
рис.11.12:
ПВ
заданного
случайного процесса в соответствии с
полученным выражением показана на
рис.11.12:
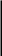
![]() W(x)
W(x)
Рис.11.12.
b 0 a x
![]()
![]()
ФРВ для случайного процесса принимающего 2 значения x=a и x=b имеет вид:
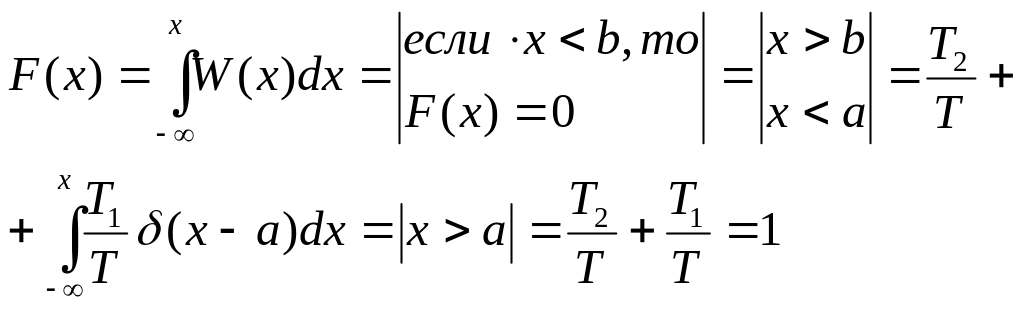
![]()
F(x)
 1
1
 T2/T1
T2/T1
 Рис.11.13.
Рис.11.13.
t
b a
Вычислим среднее значение двоичного дискретного случайного процесса, принимающего 2 значения:
x=a
c
вероятностью T1/T,
x=b
c
вероятностью T2/T