
laba_5(МЭТ-ГОТОВА)
.docxМинистерство цифрового развития, связи и массовых коммуникаций Российской Федерации
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра Электроники
Отчёт по Лабораторной работе №5
На тему: «Влияние концентрации примеси на параметры контакта двух полупроводников»
Выполнил:
Студент группы БРТ-2102
Епифанов Георгий Юрьевич
Доронина Анжела
Проверила:
Преподаватель
Каравашкина Валентина Николаевна
Москва 2022 г.
Цель работы: Исследование зависимости основных характеристик идеализированного p-n перехода от концентрации примеси.
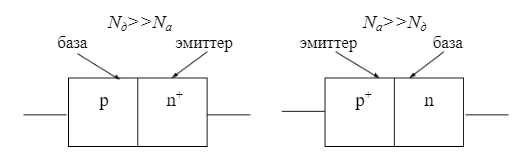
Собственное электрическое поле p-n перехода характеризуют контактной разностью потенциалов ϕk0. В идеализированном p-n переходе:
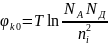
T - температура
![]() –
собственная
концентрация
–
собственная
концентрация
NA, NД – концентрации примесей
Где собственная концентрация:
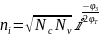
где NC, NV – эффективные плотности состояний,
ϕЗ – ширина запрещенной зоны.
ϕТ - термический потенциал
Протяженность приграничных областей с нескомпенсированными ионами примесей называют толщиной p-n перехода w. Для идеализированного p-n перехода:

εε0 – диэлектрическая проницаемость полупроводника, q – элементарный электрический заряд.
Анализ процессов в идеализированном p-n переходе приводит к так называемой формуле Шокли или теоретической ВАХ:
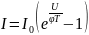
где I0 – тепловой ток (ток насыщения), I и U – ток и напряжение перехода. Величина I0 определяет величины Iпр и Iобр не только идеализированного, но и в значительной степени реального p-n перехода. Для идеализированного p-n перехода:
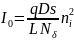 ,
,
где D – коэффициент диффузии, S – площадь p-n перехода,
L – диффузионная длина, Nб – концентрация примеси в базе.
Значения I0 изменяются в больших пределах в зависимости от типа полупроводника, площади, особенностей изготовления и температуры p-n перехода.
В зависимости от толщины p-n перехода в нём возникает лавинный или, в очень тонких p-n переходах, туннельный пробой. Напряжение лавинного пробоя Uпроб.л можно рассчитать по приближенной формуле:
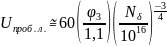
Напряжение туннельного пробоя Uпроб.т определяется выражением:
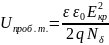
Для идеализированного p-n перехода в отсутствие напряжения барьерная ёмкость определяется соотношением:
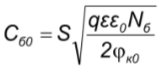
Исходные данные |
||||||
Тип п/п |
Si |
|||||
S, см2 |
3*10–7 |
|||||
Характеристики p-n перехода |
Исходный вариант |
Nб*20 |
Nб *40 |
Nб *60 |
Nб *80 |
Nб *100 |
NA, см–3 |
3*1016 |
6*1016 |
12*1016 |
18*1016 |
24*1017 |
3*1017 |
NД, см–3 |
3*1018 |
3*1018 |
3*1018 |
3*1018 |
3*1018 |
3*1018 |
Результаты при Т = 300 К |
||||||
ϕk0, В |
8,12E-1 |
8,6E-1 |
9E-1 |
9,1E-1 |
9,2E-1 |
9,3E-1 |
w, мкм |
5,9E-1 |
1,4E-1 |
1E-1 |
8,5E-2 |
7,4E-2 |
6,7E-2 |
I0, А |
2E-21 |
2,7E-22 |
2,8E-22 |
2,88E-22 |
2E-22 |
1,7E-22 |
Uпроб.л., В |
4,7E+1 |
4,98 |
2,9 |
2,1 |
1,7 |
1,4 |
Uпроб.т., В |
9,9E+1 |
4,97 |
2,4 |
1,6 |
1,24 |
9,9E-1 |
Сб0, Ф |
5,8E-13 |
2,27E-14 |
3,1E-14 |
3,87E-14 |
4,35E-14 |
4,36E-14 |
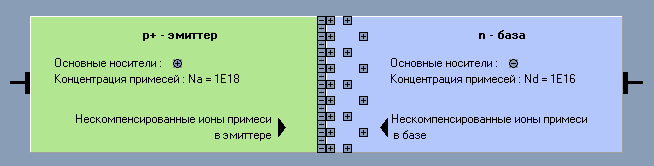
P-N переход
Исходные данные |
||||||
Тип п/п |
Si |
|||||
S, см2 |
3·10–7 |
|||||
Характеристики p-n перехода |
Исходный вариант |
N*20 |
N*40 |
N*60 |
N*80 |
N*100 |
NД =NA, см–3 |
3·1015 |
6·1016 |
12·1016 |
18·1016 |
24·1016 |
3·1017 |
Результаты при Т = 300 К |
||||||
ϕk0, В |
6,3E-1 |
7,8E-1 |
8,24E-1 |
8,45E-1 |
8,6E-1 |
8,7E-1 |
w, мкм |
7,4E-1 |
1,8E-1 |
1,3E-1 |
1,11E-1 |
9,7E-2 |
8,7E-2 |
I0, А |
1,6E-21 |
3,2E-22 |
2,2E-22 |
1,8E-22 |
1,5E-22 |
1,3E-22 |
Uпроб.л., В |
4,7E+1 |
4,98 |
2,9 |
2.1 |
1,76 |
1,4 |
Uпроб.т., В |
9,9E+1 |
4,97 |
2,4 |
1,6 |
1,24 |
9,9E-1 |
Сб0, Ф |
6E-15 |
2,4E-14 |
3,3E-14 |
4E-14 |
4,6E-14 |
5,1E-14 |

Вывод:
В ассиметричном переходе увеличение концентрации примеси в базе уменьшает напряжение пробоя и увеличивает барьерную емкость
В симметричном переходе увеличивается тепловой ток, напряжение пробоя и увеличивается барьерная емкость
Зависимость контактной разности потенциалов от концентрации примесей в обоих случаях экспоненциальная
