
Konspekt_Tv_2020_ch_6
.pdfКонспект лекций по теории вероятностей и математической статистике.
Авторы: Лохвицкий М.С., Синева И.С. 3 семестр 2020/2021 учебный год.
Лектор – Лохвицкий Михаил Сергеевич Часть 6
5.Совместное распределение случайных величин
При решении многих практических задач приходится изучать не одну случайную величину, а две, три и т.д. С.В. При этом необходимо анализировать их совместное поведение. Можно считать каждую С.В. координатой некоторого вектора и рассматривать многомерные С,В. При изучении многомерных случайных величин обобщаются все основные понятия теории вероятностей, которые были рассмотрены в предыдущих разделах. Это будет проиллюстрировано на простейшем случае двух случайных величин.
5.1. Совместное распределение двух случайных величин
5.1.1. Система дискретных случайных величин
Самой полной характеристикой для системы С.В. является закон распределения вероятностей, который устанавливает соответствие между
парами значений случайных величин { |
} и вероятностями |
|
их принятия * |
+ Этот закон можно записать в |
|
виде таблицы с двумя входами |
|
|
Таблица 5.1
⁄ |
|
|
… |
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
… |
… |
… |
… |
… |
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
Где |
{ |
|
} |
|
|
|
|
Так как события { |
|
} * |
|
+ |
бразуют |
||
полную группу, то сумма их вероятностей равняется 1: |
|
|
|||||
|
∑ |
∑ |
|
|
|
|
(5.1) |
Из двумерного закона распределения можно получить одномерные |
|||||||
законы распределения составляющих X и Y. Так событие * |
+ |
||||||
можно представить в виде суммы несовместных событий |
{ |
|
|||||
}. Поэтому |
|
|
|
|
|
|
|
|
* |
+ = ∑ |
{ |
} |
|
|
(5.2) |
Т.е. для нахождения вероятности |
нужно сложить все вероятности |
||||||
|
i-ой строчки в таблице двумерного закона. |
|
|
|
|||
Аналогично, Т. для нахождения вероятности |
нужно сложить все |
||||||
вероятности |
j-го столбца в таблице двумерного закона |
|
|
||||
|
{ |
} = ∑ |
{ |
} |
|
|
(5.3) |
Пример 5.1. В сессию студент сдает зачет и экзамен. Введем случайную величину X, принимающую два значения: 0, если зачет не сдан и 1, если зачет сдан. Величина Y - оценка на экзамене * +. Закон распределения двумерной СВ приведен в таблице 5.2

⁄ |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
0 |
0,1 |
0,1 |
0 |
0 |
0,2 |
|
|
|
|
|
|
1 |
0 |
0.1 |
0,3 |
0,4 |
0.8 |
|
|
|
|
|
|
|
0,1 |
0,2 |
0,3 |
0,4 |
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
Замечание. Для нахождения одномерных законов распределения удобно таблицу двумерного закона (таблица 5.1) дополнить окаймляющими строчкой (строчка вероятностей для с.в. X ) и столбцом (столбец вероятностей для с.в. Y). Запишем одномерные законы:
Таблица 5.3.
X |
|
0 |
|
|
1 |
|
p |
|
0,2 |
|
|
0,8 |
|
Таблица 5.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
2 |
|
3 |
4 |
|
5 |
p |
0,1 |
|
0,2 |
0,3 |
|
0,4 |
5.2. Функция распределения двумерной случайной величины
Определение 5.1. Совместной функцией распределения случайных величин X и Y, заданных на одном и том же вероятностном пространстве, называется функция
( |
) |
* |
+ |
(5.4) |
|
|
|
|
|
Геометрически функция распределения совпадает с вероятностью попадания в заштрихованную область на рисунке 5.1.
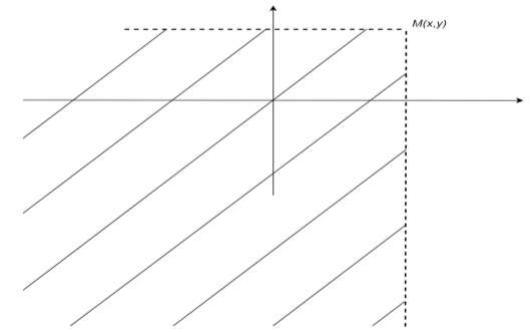
Рисунок 5.1. Область попадания для функции распределения.
Для нахождения вероятности попадания в произвольную областьV нужно использовать формулу попадания в прямоугольник G . А затем область V можно сколь угодно точно представить в виде объединения прямоугольников.
G = {(x, y) : a x < a, b y < b }. Пунктирные линии на рисунке соответствуют тому, что данная граница не включается в область, а сплошные – тем, что содержатся в области G.
Вероятность попадания в полосу равна разности значений функции
распределения в точках |
( |
) |
( |
) Так как эта полоса дополняет |
||
область с «вершиной» |
( |
) |
до области с «вершиной» |
( |
) |
|
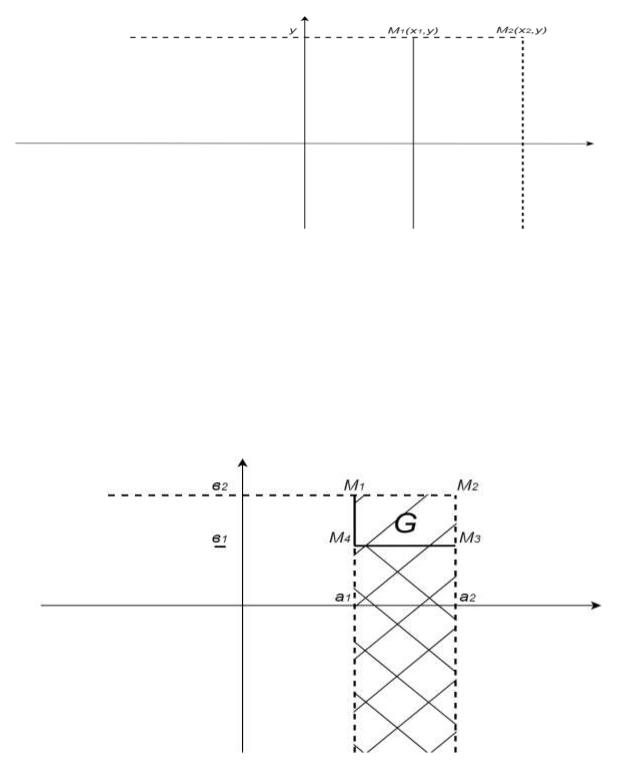
Рисунок 5.2. Вероятность попадания в полосу.
А вероятность попадания в прямоугольник равна разности вероятностей
попадания в две полосы: первая полоса с «вершинами» в точках |
(a, b) и |
||||
(a1, b2), вторая полоса с «вершинами» в точках (a, b ) и |
(a, b ). В |
||||
итоге получаем формулу: |
|
|
|
|
|
P((x, y) G) = |
(a, b) – |
(a, b ) |
(a, b ) + |
(a, b ). |
|
Рисунок 5.3. Вероятность попадания в прямоугольник.
Свойства функции |
(x, y) : |

1. |
( |
) |
* |
+ |
* |
+ |
( ) |
( )
)  *
* +
+  *
* +
+ 
 (
( ).
).
Таким образом, зная совместное распределение двух случайных величин X и Y, можно найти одномерное распределение этих случайных величин, но
обратное утверждение неверно! |
|
|
||
2. |
( |
) |
( ) |
( ) |
3. |
( |
) |
|
|
4. |
(x, y) является монотонно |
неубывающей и |
непрерывной слева |
|
функцией по каждой из переменных x и y. |
|
|
|
|||||||||||||||||||||||||||||||||||
Определение 5.2. Если |
(x, y) непрерывна и дифференцируема, то еѐ |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вторая |
смешанная производная |
|
|
|
( |
|
) |
|
|
|
(x, y) |
называется |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
совместной плотностью распределения с.в. X и Y. |
|
|
|
|||||||||||||||||||||||||||||||||||
Свойства функции |
( |
|
) : |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
1. |
|
|
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
|
|
|
|
|
|
( |
|
) |
|
|
|
|
|
где |
условие |
|
|
означает, |
что хотя |
бы одна из |
|||||||||||||||||
|
координат x и y стремится к |
|
|
(т.е. точка (x, y) бесконечно удаляется |
||||||||||||||||||||||||||||||||||
|
от начала координат). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3. |
P |
* |
( |
|
|
|
) |
|
|
|
+ |
= |
|
|
|
|
|
|
( |
|
|
) |
|
|
|
|
, где B –множество на плоскости. |
|||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. |
|
|
|
|
( |
|
|
) |
|
|
∫ |
|
|
|
|
∫ |
|
|
|
|
|
( |
|
|
) |
|
|
|
|
|
|
|
|
(5.5) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это свойство частный случай свойства 3: область В – часть плоскости x >
u, y > v . Геометрически это означает, что |
(x, |
y) |
численно равна |
объѐму области, ограниченной поверхностью |
z |
= |
(u, v), |
плоскостью z = 0, и полуплоскостями x > u, y > v (см. рисунок 5.4).

Рисунок.5.4. Геометрическая интерпретация связи |
(x, y) и |
(x, y). |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
∫ |
|
∫ |
|
|
|
( |
) |
|
|
= 1 |
(условие нормировки). |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следует из свойства 3: в этом случае область В –вся плоскость |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
|
|
( |
|
) |
|
∫ |
|
|
|
( |
|
|
) |
; |
|
(5.6) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
( |
|
) |
|
∫ |
|
|
( |
|
|
) |
|
|
|
|
|
(5.7) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(т.е. по совместной плотности распределения можно восстановить одномерные плотности распределения, но обратное неверно!) Докажем формулу (5.6).
( ) |
( |
) ∫ |
∫ |
( ) |
Возьмем производную от обеих частей этого равенства по переменной x. Используем теорему о производной интеграла по переменному верхнему пределу: производная равна подынтегральной функции, в которую вместо переменной подставлено значение верхнего предела. В данном случае подынтегральная функция - это внутренний интеграл от , в который вместо переменной интегрирования u подставили верхний предел, равный х
( ) |
|
( ) |
|
{∫ |
∫ |
( ) } |
∫ |
|
( |
|
) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Пример 5.2. Совместное |
распределение |
случайных |
величин задано |
|
|
( |
) |
|
|
плотностью распределения |
(x, y) = { |
|
|
|
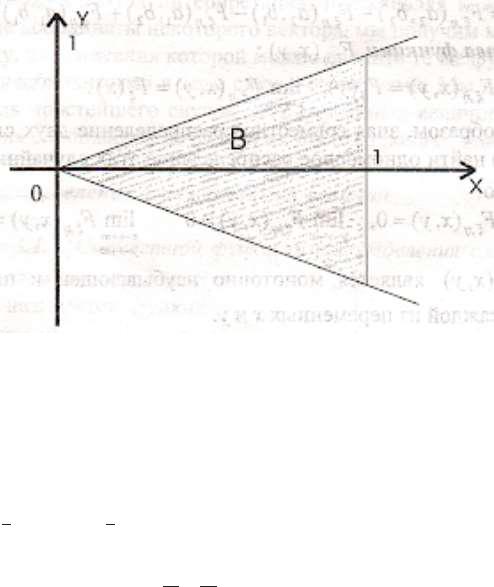
Найти вероятность попадания с.в. в область В: |
P( ( |
) B), где |
||
B={(x, y) : |y| |
} (см. рисунок 5.5). |
|
|
|
Рисунок 5.5. Область B в примере 5.2.
В соответствии со свойством 6 (интегрирование только по верхнему треугольнику, т.к. в остальной области двумерная плотность равна 0):
P(( |
|
) |
B)= |
∫ |
∫ |
( |
) |
|
∫ |
∫ |
|
|
|
|
|||||||
∫ |
( |
) |
∫ |
( |
|
) |
. |
|
|
/ |
|
|
|
Пример 5.3. Случайная величина равномерно распределена внутри
эллипса: B ={(x, y) : }
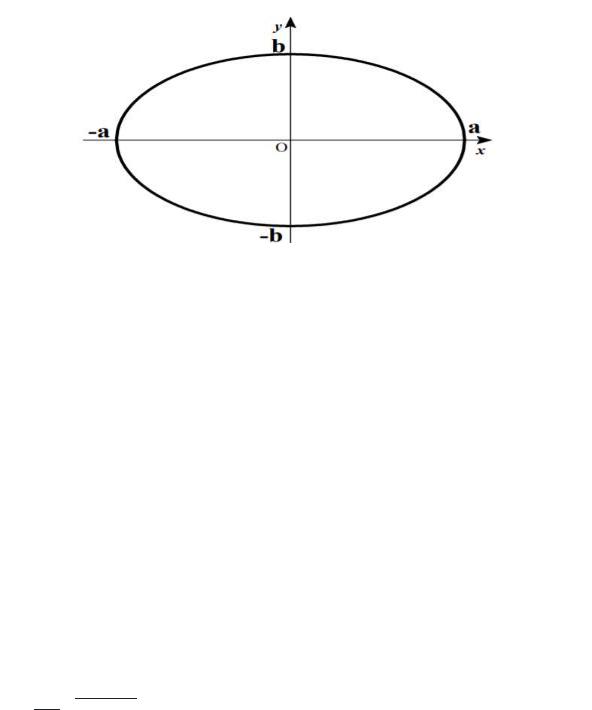
Рисунок 5.6. Эллипс к примеру 5.3.
Найти одномерные плотности распределений. Решение. Двумерная плотность имеет вид:
(x, y) = { |
. |
Постоянную С найдем из условия нормировки плотности (свойство 5)
|
∫ |
∫ |
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
⁄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Интеграл |
берется по |
области В, ограниченной эллипсом. S – площадь |
|||||||||||||||||||||||
области В, равная |
|
Одномерная плотность по формуле (5.6) |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
( |
) |
∫ |
( |
) |
|
∫ |
|
|
√ |
|
|
|
|
= |
|
√ |
|
|
при |
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|x| |
; и 0 в противном случае: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
√
(x) = {

Рисунок 5.7. Одномерная плотность распределения примера 5.3.
Аналогичное выражение для второй одномерной плотности:
√
(y) = {
Задача 5.1. Двумерная с.в. равномерно распределена, однако, одномерные распределены не равномерно. Дайте объяснение этому факту.
5.3. Независимость случайных величин
Обсуждая в предыдущем разделе связь между одномерными функциями (плотностями) распределения компонент и их совместной функцией (плотностью) распределения, мы подчѐркивали, что по совместному распределению можно восстановить распределения компонент, но обратное в общем случае невозможно.
В данном разделе мы рассмотрим тот частный случай, когда по одномерным распределениям компонент можно восстановить их совместное распределение. В этом частном случае расчѐты значительно упрощаются (например, двойные интегралы заменяются на произведение простых).
Определение 5.3. Случайные величины X и Y независимы, если для любых x, y
|
( |
|
) |
|
( |
|
) |
|
( |
) |
(5.8) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
