
Теоретические основы химической технологии (ответы на билеты)
.pdf
7. Понятие об энергопреобразующем устройстве (ЭПУ), примеры ЭПУ. Принципиальная схема ЭПУ. Энергетический и энтропийный балансы ЭПУ, к.п.д. стационарного ЭПУ. К.п.д. идеальных ЭПУ на примерах: фотоэлектрический преобразователь, топливный элемент, механический генератор электрической энергии.
Энергопреобразующее устройство (ЭПУ) – устройство, генерирующее,
перераспределяющее потоки или преобразующее одну форму энергии в другую (неквалифицированную в квалифицированную).
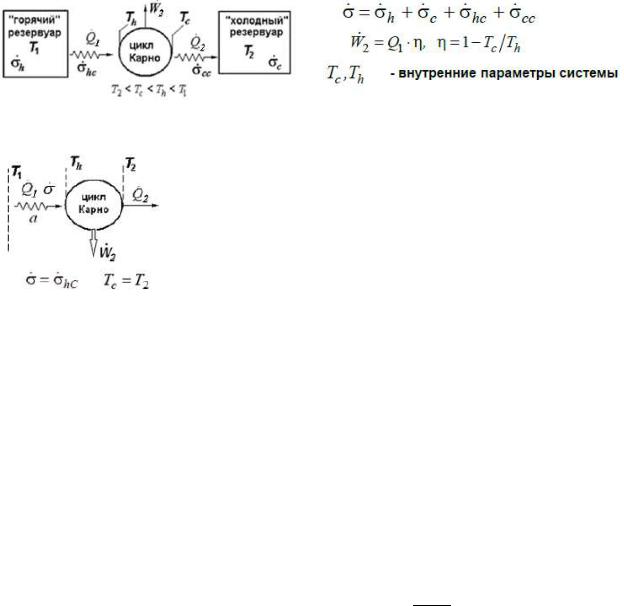
Принципиальная схема стационарного ЭПУ:
Энергетический и энтропийный баланс ЭПУ с учётом обозначений:
Продукты ЭПУ в случае генерирования квалифицированной энергии это поток квалифицированной энергии W2 и тепловой поток Q2, который, помимо всего, отводит энтропию, произведенную вследствие неидеальности ЭПУ. Возникает задача об оптимальном соотношении между W2 и Q2.
КПД стационарного ЭПУ
|
|
|
|
|
|
|
|
( ) |
+ ̇+ ̇ |
− |
|
|
поток преобразуемой энергии |
|
|
|||||||||||||
̇ = ∆ ̇+ ∆ ̇ |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̇ |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
( ) |
|
|
|
( ) |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
̇= ∆ ̇ |
|
+ ∆ ̇ |
+ |
|
|
− сопряжённый ему поток энтропии |
|
|
||||||||||||||||||||
|
̇ |
|
|
|
|
̇ |
|
1 |
|
̇ |
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
= |
|
|
= (1 − |
|
|
|
) − |
|
− |
|
эффективность ЭПУ (КПД) |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
̇ |
|
|
|
|
|
̇ |
|
|
|
|
|
̇ |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̇ |
|
Для идеального (обратимого) ЭПУ ̇= 0 и соответственно КПД равно = (1 − |
2 |
) |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̇ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КПД идеальных {необратимых} ЭПУ |
|
|
||||||||
1) Машина Карно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
̇ = ̇ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
̇ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
̇= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
̇ |
|
|
̇ |
|
|
|
|
|
̇ |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (1 − |
|
2 |
) {− |
|
2 |
} = (1 − |
|
|
2 |
) {− |
2 |
} |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
̇ |
|
|
|
̇ |
|
|
|
|
1 |
̇ |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2) Электромотор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
̇ = ̇ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
̇= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
̇ |
|
|
̇ |
|
|
|
̇ |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (1 − |
|
2 |
) {− |
|
2 |
} = 1 {− |
|
|
2 |
} |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
̇ |
|
|
|
̇ |
|
|
|
|
̇ |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|

3) Топливный элемент
̇ = ∆ ̇̇= ∆ ̇( )
|
̇ |
̇ |
∆ ̇ |
|
̇ |
|||
|
|
|
|
( ) |
|
|
|
|
= (1 − |
2 |
) {− |
2 |
} = (1 − |
2 |
) {− |
2 |
} |
|
|
∆ ̇ |
|
|||||
|
̇ |
̇ |
|
∆ ̇ |
||||
4) Фотоэлектрический преобразователь
̇ = ∆ (̇) = ( 14 − 24) 4
̇= ∆ ̇( ) = 3 ( 13 − 23)
= 5,67 × 10−8 |
Дж |
− постоянная Стефана − Больцмана |
с∙ 4 |
|
̇ |
̇ |
∆ ̇ |
̇ |
||||
|
|
|
|
( ) |
|
|
||
= (1 − |
2 |
) {− |
2 |
} = (1 − |
2 |
) {− |
2 |
} |
|
|
( ) |
( ) |
|||||
|
̇ |
̇ |
∆ ̇ |
∆ ̇ |
||||
8. Тепловая машина, примеры тепловой машины. Схема реальной тепловой машины. Основное отличие тепловой машины от машины Карно. Адекватная схема тепловой машины. Принцип максимальной мощности А.И.Алиханова. К.п.д. адекватной тепловой машины: формула И.И.Новикова как обобщение формулы С.Карно. Задача.
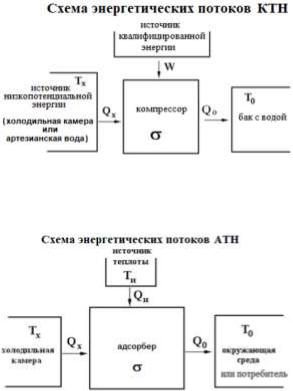
Тепловая машина представляет собой ЭПУ, преобразующего поступающий от источника теплоты (нагревателя) тепловой поток ̇1 с температурным потенциалом T1 в передаваемый внешнему потребителю поток квалифицированной энергии ̇2 и передаваемый в холодильник тепловой поток ̇2 с температурным потенциалом T2 < T1
Тепловая машина состоит из генератора квалифицированной энергии и генератора энтропии в составе двух резервуаров теплоты - «горячего» и «холодного», двух теплообменных устройств между генератором и резервуарами теплоты. Генератор квалифицированной энергии представим идеальным циклом Карно. Генерация энтропии сосредоточена, во-первых, в тепловых резервуарах,
̇ |
и ̇, где она обусловлена необходимостью обеспечить требуемые потоки теплоты с |
|
|
постоянными температурами, и во-вторых, в теплообменниках при переносе теплоты между
тепловыми резервуарами и циклом Карно, ̇ и ̇ . Теплообменные устройства и тепловые
резервуары работы не производят, следовательно, эффективность и мощность тепловой машины равна эффективности и мощности цикла Карно
Принцип Алиханова–Новикова: при заданных внешних условиях оптимальному режиму функционирования тепловой машины соответствует её максимальная мощность (максимальная мощность генератора ̇2).
В качестве адекватной модели реальной тепловой машины рассмотрим ЭПУ составленное из идеального цикла Карно и единственного теплообменного устройства , передающего тепловой поток ̇1 от горячего термостата с температурой T1 к циклу Карно при
температуре Th на изотермической стадии получения теплоты циклом |
|
Карно. Резервуары теплоты – идеальные термостаты ( ̇ = ̇ = 0); |
|
|
|
теплообмен с холодным термостатом – обратимый (Tc = T2, ̇ |
= 0). |
|
|
Вычисление к.п.д. упрощенной схемы тепловой машины на основе Принципа Алиханова
Из общей теории теплообмена следует выражение для потока теплоты ̇1
̇ = |
∙ ( |
− )+1 |
|
||
1 |
|
1 |
|
Дж |
|
|
− размерная величина |
||||
|
|||||
м2∙с∙К( +1) |
|||||
|
|
|
|
||
n – параметр Нуссельта, характеризующий механизм переноса в теплообменном устройстве
КПД тепловой машины равен КПД цикла Карно.
безразмерные параметры = |
|
|
, |
= |
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|||
= 1 − |
= 1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда мощность тепловой машины равна |
|
|
||||||||||||||||
̇ = ∙ ̇ = (1 − |
|
2 |
) ∙ |
∙ ( − )+1 |
= ̇( ) |
|
||||||||||||
|
|
|
||||||||||||||||
2 |
1 |
|
|
|
|
|
|
1 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По принципу максимальной мощности: |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
̇ |
|
|
|
|
|
|
||||
̇ = ̇( ) |
|
|
|
|
2 |
= 0 |
2 |
− ∙ |
|
|
||||||||
|
|
|
|
|
|
|||||||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
+ 1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решая полученное уравнение получаем: |
|
|
||||||||||||||||
Для дальнейшего упрощения введём
1 − + 1 = 0

( ) = |
|
|
+ √ 2 |
|
2 |
+ |
1 |
|
|
||||
2( + 1) |
|
4( + 1)2 |
+ 1 |
||||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
2( + 1) |
(1 + √1 + |
4( + 1) |
|
|||||||
= 1 − |
= 1 − |
) |
|||||||||||
|
|
|
|
||||||||||
|
|
|
2 |
||||||||||
Формула Новикова – КПД тепловой машины в случае линейного теплообмена = 0 :
= 1 − √ = 1 − √ 21
Энергетическая эффективность тепловой машины:
̇= ̇ 0 = 0 ∙ 1 −̇2 1
9. Принцип действия и назначение теплового насоса (ТН). Основные типы ТН, схемы энергетических потоков. Энергетический и энтропийный балансы ТН. Эффективность ТН, используемых как нагреватель и как холодильник, эффективность идеальных тепловых насосов.
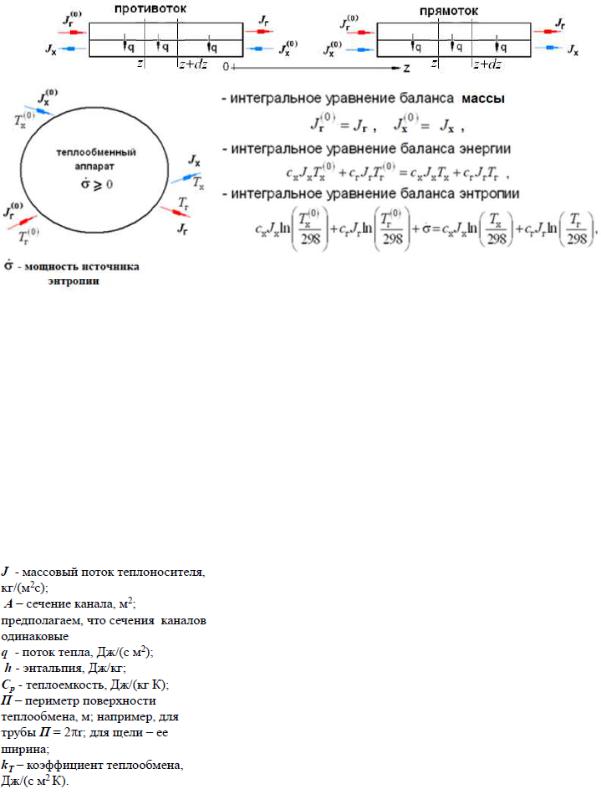
Тепловой насос – энергопреобразующее устройство, предназначенное для повышения потенциала (температуры) теплоты, отбираемой от низкопотенциального источника. После повышения потенциала теплоту можно передать потребителю, заинтересованному в теплоте с высокой температурой, или рассеять в окружающую среду, если целью теплового насоса является производство «холода».
Тепловой насос функционирует по типу включенного «в обратную сторону» обратимого цикла Карно, следствием чего оказывается передача теплоты «горячему» термостату от «холодного» термостата, сопровождаемая затратами энергии внешнего источника.
Типы тепловых насосов
1) Компрессионный тепловой насос (КТН) использует квалифицированную энергию для сжатия потока пара рабочего тела для повышения его температуры (рабочее тело –жидкий хладагент). В КТН движущей силой потока пара является разность давлений пара в испарителе холодильной камеры и на «всасывающем входе» в компрессор.
̇ + ̇= ̇ |
|
|
|||||||
|
|
|
|
0 |
|
|
|||
{ ̇ |
|
|
̇ |
|
|
||||
|
|
+ ̇= |
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
Эффективность идеального КТН ( ̇= 0) |
|||||||||
|
|
|
̇ |
|
|
|
|
||
(ктн) = |
|
|
= |
|
|
|
|
||
хол |
̇ |
|
|
|
− |
||||
|
|
|
|
|
0 |
|
|||
|
|
|
̇ |
|
|
|
|
||
(ктн) = |
0 |
|
= |
|
|
0 |
|
||
нагр |
̇ |
|
|
− |
|||||
|
|
|
|
|
0 |
|
|||
2) Адсорбционный тепловой насос (АТН) использует неквалифицированную энергию (теплоту) для регенерации адсорбента. В АТН движущей силой потока пара рабочего тела (рабочее тело – жидкий адсорбтив) является разность химических потенциалов адсорбтива в испарителе холодильной камеры и в адсорбенте.
|
̇ + ̇ = ̇ |
|
|
|
|
||||||||||
|
|
|
н |
|
0 |
|
|
|
|
|
|||||
{ ̇ |
̇ |
|
|
|
̇ |
|
|
||||||||
|
|
+ |
|
н |
+ ̇= |
|
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
н |
|
|
|
|
0 |
|
|
|
||||
Эффективность идеального КТН ( ̇= 0) |
|||||||||||||||
|
|
|
|
|
̇ |
|
|
( − ) |
|||||||
(ктн) = |
|
|
|
|
= |
|
н |
0 |
|
|
|||||
|
хол |
|
|
|
̇ |
|
|
( |
− ) |
||||||
|
|
|
|
|
н |
|
0 |
|
|
н |
|||||
|
|
|
|
|
̇ |
|
|
( |
− ) |
||||||
(ктн) = |
|
0 |
|
= |
|
н |
|
|
0 |
|
|||||
|
нагр |
|
|
|
̇ |
|
|
( |
− ) |
||||||
|
|
|
|
|
н |
|
0 |
|
|
н |
|||||
10. Теплообменный аппарат, технологическое назначение. Прямоточные и противоточные теплообменные аппараты. Уравнения материального, энергетического и энтропийного балансов теплообменного аппарата с двумя теплоносителями. Эффективность теплообменного аппарата. Математическая модель противоточного теплообменного аппарата. Безразмерная математическая модель противоточного теплообменного аппарата, эффективность противоточного теплообменного аппарата.
Теплообменный аппарат – ЭПУ, технологическая задача которого заключается в максимально полном обмене энтальпией между потоками теплоносителей. По организации
потоков теплоносителей различают прямоточные и противоточные теплообменные аппараты:
В безразмерных координатах (см. ниже):
+ = х + г + ̂ = х + г
Эффективность теплообменного аппарата можно представить в виде отношения нагрева холодного теплоносителя в реальном аппарате к нагреву в лучшем при данных условиях устройстве:
|
( ) |
− (0) |
|
= |
х |
х |
|
( ) |
− (0) |
||
|
|||
|
х |
х |
Наилучшим аппаратом не является «идеальный аппарат» с нулевой генерацией энтропии поскольку, решая соответствующую систему уравнений получим что температура горячего потока на выходе ниже температуры холодного на входе, что в действительности невозможно. Такой результат получается в следствие того, что любой теплообмен генерирует энтропию (при обратимом теплообмене – работу).
Рассмотрим противоточный теплообменный аппарат, в котором потоки теплоносителей направлены вдоль оси каналов и движутся с постоянной скоростью, а сам аппарат работает в стационарном режиме (то есть нет изменений во времени). Таким образом все изменения в таком аппарате возможны лишь вдоль оси аппарата z.
Локальные уравнения энтальпийного баланса примут вид:
г г = |
х х = |
Поток тепла между теплоносителем и поверхностью можно представить выражением:
= (г − х)
Пренебрегая зависимостью энталипии теплоносителя от давления можно записать:
|
= |
г |
|
= |
|
|
= |
х |
|
= |
|
|
|
||||||||||
г |
|
|
г |
,г |
г |
х |
|
|
х |
,х |
х |
|
|
|
|
|
|
|
|
|
|

С учётом записанных выражений энтальпийный баланс приводится к виду, с учётом граничных условий:
|
|
г |
|
= − |
( − ) |
||||
|
|||||||||
г |
,г |
|
|
|
|
г |
х |
||
|
|
х |
|
= − |
( − ) |
||||
|
|
||||||||
х |
,х |
|
|
|
|
г |
х |
||
{ |
(0) = (0) |
( ) = |
(0) |
||||||
г |
|
г |
|
|
х |
х |
|||
Полученная система уравнений представляет собой математическую модель противоточного аппарата. Характерные особенности каждой конкретной задачи можно свести к одному параметру, имеющему название Высоты Единицы Переноса (ВЕП). Этот параметр представляет собой внутренний геометрический масштаб системы. На основе ВЕП можно ввести безразмерные параметры Z (безразмерная координата) и N (безразмерная длина теплообменника – число единиц переноса). Чем выше число единиц переноса тем более эффективно проходит теплообмен.
|
|
|
(0) |
|
|
|
|
|
|
|
|
||
= |
г г |
= |
х |
|
= |
|
х |
|
= |
г |
− безразмерные параметры системы |
||
|
|
|
|
|
|
||||||||
|
х х |
|
г(0) |
|
|
х |
г(0) |
г |
г(0) |
|
|||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
В новых безразмерных координатах математическая модель |
||||||
|
|
|
|
|
|
|
|
|
|
|
теплообменного аппарата примет вид: |
||
|
|
|
|
|
г |
|
= −( |
|
− ) |
|
|
||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
г |
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
= −( |
|
− ) |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
г |
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ г( = 0) = 1 |
х( = ) = |
|||||||||
Представим эффективность противоточного теплообменника через безразмерные величины:
|
( ) |
− (0) |
|
( ) |
− |
|
= |
х |
х |
= |
х |
|
|
( ) |
− (0) |
( ) |
− |
|||
|
|
|||||
|
х |
х |
|
х |
|
В связи с тем, что при возрастании числа единиц переноса, повышается эффективность теплообменника, в качестве лучшего (эталонного) теплообменника рассматривается теплообменник бесконечной длинны. Тогда выражение для КПД можно переписать в виде:
( )(0) −
= х(∞)(0) −х
Решив написанную выше систему уравнений и подставив решение в выражение для КПД получим:
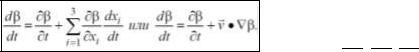
11. Элементы механики сплошной среды. Потоки жидких и газовых масс в химической технологии. Описание движения по Лагранжу и Эйлеру. Субстанциональная производная. Закон сохранения массы (уравнение неразрывности). Условия несжимаемости среды, выраженное через поле скорости.
Элементы механики сплошной среды:
В сплошной среде присутствуют силы:
а) Внутренние силы – между частицами выделенного объема, взаимно скомпенсированы по 3-ему з-ну Ньютона.
б) Внешние силы – действующие на жидкость внутри объёма, подразделяющиеся на объемные силы (массовые – дальнодействующие – сила тяжести и Лоренца) и поверхностные (близкодействубщиесила давления и вязкости).
Потоки жидких и газовых масс в ХТ:
Элементы механики сплошной среды: под сплошной средой понимаются жидкие, газовые и деформируемые твёрдые тела. Они обладают следующими характеристиками:
инертность – свойство, характеризуемое массой
вязкость – движение среды, сопровождающееся диссипацией энергии (определяет гидравлическое сопротивление)
сжимаемость – свойство среды, приводящее к звуковым, ударным и детонационным волнам
Поэтому в механике сплошных сред (МСС) изучают реакцию сплошной среды на внешние воздействия, приводящие к движению жидких и газовых масс. Для анализа сплошных сред в МСС используют: подход Лагранжа и Эйлера.
Описание движения по Лагранжу и Эйлеру:
А) Подход Лагранжа: мысленно выделяют в потоке жидкости или газа элементарные частицы и описывают их движение с использованием законов механики Ньютона. Проследив за движением всех лагранжевых частиц, можно построить их траектории, множество таких траекторий и будет исчерпывающим описанием движения сплошной среды.
( ) = { 1( ), 2( ), 3( )}
Б) Подход Эйлера: в каждой точке пространства в разные моменты времени изучаются параметры движения, измеряется скорость. Скорость во всех точках пространства образуют поле скоростей. Далее строят линии тока – касательные к векторам поля скоростей. В стационарных условиях линии тока и траектории совпадают. ( , 1, 2, 3)
Субстациональная производная:
Так называют математический опрератор, устанавливающий соответсвие между подходами Лагранжа и Эйлера. Причина этому: при использовании Элерского подхода необходимость записывать в Эйлеровых перменных величины, характеризующие индивидуальные (Лагранжевые) частицы жидкости.Рассмотрим некий параметр β(t, x1,x2,x3) – характеризующий ствойство частицы. Тогда производная по времени будет β(t, x1(t), x2(t), x3(t)) – представляет собой скорость изменения параметра β Лагранжевой частицы вдоль её траектории.
,где = ( 1 , 2 , 3) – скорость частицы.
Левая часть формулы относится к подходу Лагранжа, а правая часть – к подходу Эйлера. Часто данную производную называют локальной производной, в то время как полную производную, характеризующую скорость изменения параметра β вдоль Лагранжевой частицы называют
субстациональнойй производной.
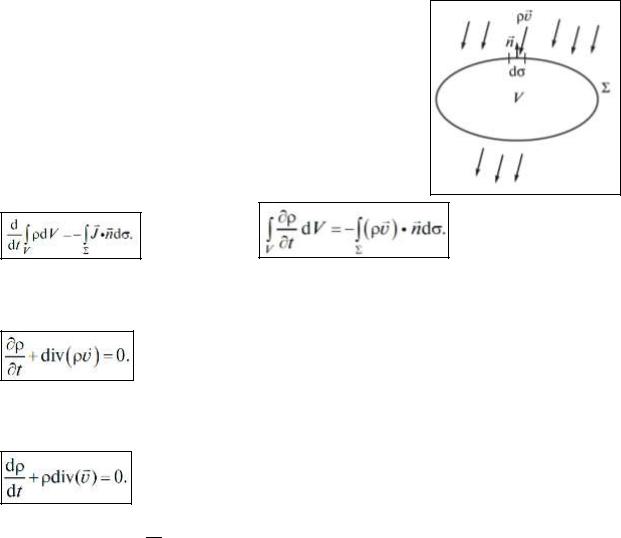
Закон сохранения массы (уравнение неразрывности):
В области пространства, заполненной движущейся жидкостью, выделяют некоторый обём V, ограниченный замкнутой поверхностью. Ориентация каждого элемента поверхности задается единичным вектором n, нормальным к выбранному элементу. Если элементарная площадка является частью замкнутой поверности, то оиентацию площадки задают внешней нормалью. Вектор ndσ, где dσ – площадь элемента поверхности, полностью характеризует элемент поверхности. Из закона сохранения массы следует, что скорость изменения массы жидкости, заключенной в выделенном объёме, определяется исключительно массовыми потоками через ограничивающую поверхность:
, так как V=const
Знак « – » в правой части обусловлен тем, что при положительных pv*n происходит вынос массы из рассматриваемого объёма.Затем заменил поверхностный интерграл интегралом по объёму и устремив объём к нулю, в результате получим локальное уравнение сохранения массы сплошной среды или уравнение неразрывности:
Условия несжимаемости среды, выраженное через поле скорости:
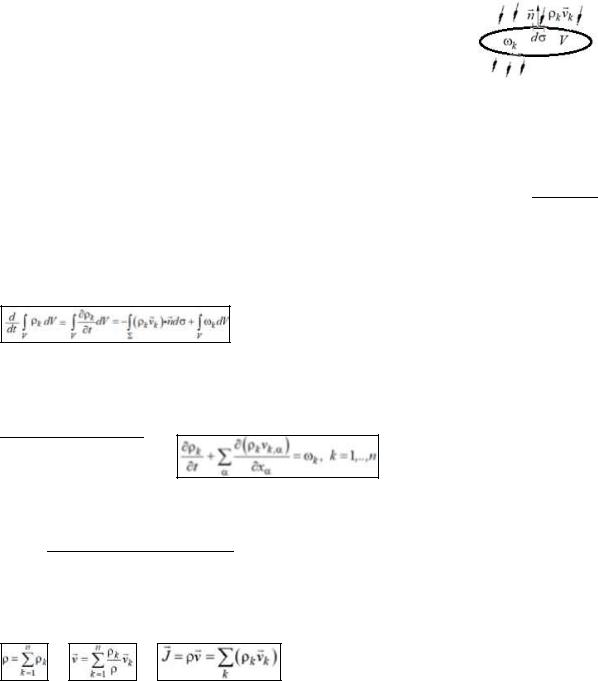
Если на уравнение неразрыност и применить формулу векторного анализа div(v) = v* ρ+ρ*div(v)
и определение субстанциональной производной, то получим уравнение неразрывности для лагранжевой частицы:
По определению среда является несжимаемой, если плотность лагранжевой частицы неизменна во времени. = 0 Отсюда мы получаем условие несжимаемости: ( ) = 0
12. Особенности движения многокомпонентных гомогенных сред. Уравнение баланса массы компонента среды. «Эффективная» среда. Представление потоков компонентов суммой диффузионной и конвективной составляющих, линейная зависимость диффузионных потоков. Представление диффузионных потоков законом Фика, проблема линейной зависимости диффузионных потоков по Фику. Уравнение конвективной диффузии компонента среды.
Особенности движения многокомпонентных гомогенных сред:
Скорость движения компонентов среды в каждой точке пространства и в каждый момент времени описывают с помощью n векторных функций vk(r, t), состав гомогенной многокомпонентной среды в каждой точке пространства и в каждый момент времени описывают с помощью n скалярных функций, значения которых равны массовым плотностям компонентов ρk(
x1, x2, x3, t), k = 1,2,…n. Массовый поток k-го компонента равен Jk = ρkvk. Таким образом , механическое состояние многокомпонентной среды характеризуется при помощи 4n вещественных функций от пространственных координат и времени: n массовых плотностей компонентов смеси и 3n декартовых координат векторов скоростей этих компонентов.
Уравнение баланса массы компонента среды:
Используем подход Эйлера: выделяем объём в реакционном пространстве, заполенном многокомпонентной средой. В реакционной зоне скорость изменения массы каждого компонента в выделенном объеме определяется не только массовыми потоками этого компонента через ограничивающую поверхность, но и скоростью химических
превращений с участием этого компонента в рассматриваемом объёме. Поэтому рассматривается
по отдельности каждый компонент. Массовый поток k-го компонента: Jk = ρkvk
Пусть полное число химических реакций в выделенном объёме равно N, а их локальные скорости равны ξj , где ξj – координата j-й реакции. Тогда локальная массовая скорость химического
превращения k-го компонента в j-й реакции равна νkj ξj,где νkj – стехиометрический коэффициент k-го компонента в j-й реакции, умноженный на молекулярную массу k-го компонента.. Тогда полная
локальная массовая скорость превращения k-го компонента во всех реакциях равна:  Тогда скорость изменения массы k-го компонента в выделенном объёме можно представить
Тогда скорость изменения массы k-го компонента в выделенном объёме можно представить
в виде интегрального уравнения материального баланса, учитывающего массовые потоки этого компонента, пересекающие ограничивающую объем поверхность, и скорость превращения компонента в объеме:
Знак «–» обусловлен разнонаправленностью вектора потока и вектора нормали. Теперь после замены поверхностного интеграла на интеграл по объёму и перехода к пределу, где объём стремится к нулю, получаем дифференциальное уравнение, описывающее распределение плотности k-го компонента в области течения смеси (локальное уравнение распределения k-го компонента в рамках Эйлера и в декартовых координатах):
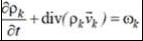 или Полученные уравнения баланса массы каждого компонента многокомпонентной смеси
или Полученные уравнения баланса массы каждого компонента многокомпонентной смеси
отличаются от уравнения неразрывности однокомпонентной жидкости слагаемым ωk , который и учитывает химические реакции. Теперь просуммировав по всем компонентам и учитывая закон сохранения массы в ходе химических превращениях, получим уравнение баланса массы среды:
 в котором отсутствуют химические реакции.
в котором отсутствуют химические реакции.
Полученное уравнение можно рассматривать как уравнение неразрывности некоторой «эффективной» однокомпонентной среды, локальные механические характеристики которой определяются: плотностью, скоростью и массовым потоком:
