Задание 1

2

получит имя "Приход", а диапазон С2:С5 - имя "Расход". Убедитесь, что теперь можно выделять эти блоки, выбирая из выпадающего списка в поле имени соответствующее имя.

Ввод табличной формулы с использованием имен диапазонов.

Задание.

1.Выделим блок D2:D5. В этом блоке активна ячейка D2.

2.Наберем знак равенства =.

3. Нажмем функциональную клавишу F3. Появится диалоговое окно "Вставка имени". Выберем имя "Приход" и щелкнем "ОК". Формула примет вид = Приход.

4.Наберем знак минус —.

5.Вновь нажмем клавишу F3. В диалоговом окне "Вставка имени" выберем имя "Расход" и щелкнем "ОК". Формула примет вид = Приход - Расход.

6.Нажмем сочетание клавиш Ctrl+Shift+Enter. Во всех ячейках блока появится формула {=Приход-Расход}.

Прокомментируем шаги. На третьем и пятом шаге мы выбирали имя из списка имен. Можно было ввести имя непосредственно с клавиатуры, но предложенный метод проще и нет риска ошибиться в наборе имени. На шестом шаге мы нажимаем не Enter, как ранее при вводе формулы, a Ctrl+Shift+Enter (при нажатии клавиши Enter должны быть нажаты обе клавиши Ctrl и Shift). Это очень важно. Если бы мы нажали Enter, то формула была бы введена только в активную ячейку блока D2. Фигурные скобки, окружающие формулу, говорят о том, что это табличная формула. Эти скобки нельзя набирать вручную (формула будет воспринята как текст)._

Ввод табличной формулы. Разумеется, табличную формулу можно вводить и без использования имен.

3

Задание. Скопируйте блок А1 :С5 в А11 :С15. Повторим все шаги. Выделим блок D12:015.

Вэтом блоке активной ячейкой является D12. Наберем знак равенства

=.Выделим блок В12:В15, наберем знак минус -, выделим блок С12:С15, нажмем сочетание клавиш Ctrl-Shift+Enter.

Во всех ячейках блока появится формула {=В12:В15-С12:С15}. Мы получили две идентичные таблицы.

Выделение блока с табличной формулой.

Задание. Выделите ячейку D2, и нажмите клавиши Ctrl+/. Будет выделен весь блок. Если проделать эту операцию над обычной ячейкой, будет выведено сообщение "Не найдено ни одной ячейки, удовлетворяющей указанным условиям".

Есть и другой способ выделения.

Задание. Нажмите клавишу F5 (эквивалент пункта меню "Правка/ Перейти"). В диалоговом окне щелкните кнопку "Выделить", установите переключатель "Текущий массив".

Изменение табличной формулы. Попытаемся очистить одну из ячеек, занятую табличной формулой.

Задание. Выделим ячейку D2 и нажмем клавишу Del. Получим сообщение "Нельзя изменять часть массива". Удалить блок можно только целиком.

Отредактировать формулу можно так: выделить блок с формулой (клавиши Ctrl+/), нажать функциональную клавишу F2, внести изменения в формулу, нажать сочетание клавиш Ctrl+Shift+Enter.

Задание. Ввести в блок формулу {=Приход - Расход - 1}, потом отменить это.

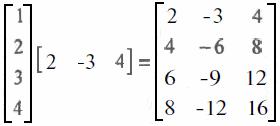
4

Задание. Перейдите на новый рабочий лист и назовите его "Константы".

В блоке (вектор-столбце) А2:А5 записать числа: 1,2,3,4. Требуется получить в блоке B2:D5 три вектор-столбца, каждый из которых представляет собой результат умножения исходного вектор-столбца на числа

2, -3, 4.

(Этот пример мы можем решить уже известным нам методом: разместить числа 2, -3, 4 в диапазоне В1:D1, записать в ячейку В2 формулу =$А2*В$1 и скопировать ее в остальные ячейки диапазона B2:D5.)

Задание. Дадим более экономное решение. Выделим блок В2:D5. Запишем в него табличную формулу {=А2:А5*{2;-3;4}}. Получится тот же результат, но мы сэкономили место на рабочем листе: теперь блок В1:D1 пуст.

Табличный массив {2;-3;4} можно интерпретировать как вектор- строку, а блок А2:А5 как вектор-столбец. Получается, что мы перемножили вектор-столбец (4 х 1) на вектор-строку (1 х 3) и получили матрицу (4x3):

Но если мы введем формулу {={2;-3;4}* А2:А5}, то получим гот же результат, хотя с позиций матричной алгебры вектор-строку (1x3) нельзя умножать на вектор-столбец (4x1) из-за несогласованности размеров (число

столбцов в первом сомножителе должно равняться числу строк во втором сомножителе).

Итак, массив чисел, разделенных точкой с запятой и заключенных в фигурные скобки, можно рассматривать как вектор-строку.

Если вместо точки с запятой использован другой разделитель — двоеточие, то массив можно интерпретировать как ветор-столбец.

5

Задание. В A10:D10 разместите числа: 1, 2, 3, 4. В блок F10:I12

поместите табличную формулу ={2;-3;4}*A10:D10. Сопоставьте с результатом предыдущего задания. Поменяйте местами сомножители и убедитесь, что результат не изменяется.

Функции, возвращающие блок Задание. Перейдите на новый рабочий лист и назовите его "Функции".

В Excel имеются функции, возвращающие сразу несколько значений. Естественно, что формулы, которые содержат такие функции, надо вводить

как табличные и перед вводом этих формул выделять нужное количество ячеек.

Подсчет распределения чисел по диапазонам значений. Функция ЧАСТОТА (исходный_ массив, массив_ интервалов) подсчитывает, сколько значений из исходного_ массива попадает в диапазон между значениями, представленными в массиве_ интервалов. Более точно, если массив_ интервалов — массив {а:Ь:с}, то числа ИСХОДНОГО массива распределяются по промежуткам:

.

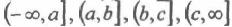Обратите внимание, что промежутки полузамкнутые, т.е., например,

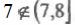, а .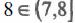

Количество промежутков на единицу больше количества элементов в массиве_ интервалов.

Задание. Введите в блок А1:А10 числа 1, 2, 2, 3, 4, 6, 5, 4, 4,3 — это исходный массив. В С1:С4 введите числа 2, 3, 4, 5 — это массив интервалов. В Е1:Е5 (количество ячеек в результате на 1 больше, чем в массиве карманов) введите табличную формулу {=ЧАСТОТА(А1:А10,С1:С4)>. Она вернет значения: 3, 2, 3, 1, 1. Проверьте этот результат. Формулу можно было ввести в виде {=ЧАСТОТА(А1:А10,{2:3:4:5})}. Тогда нет необходимости заполнять блок С1 :С4.

6

Задание. Введите числа

и подсчитайте количество двоек, троек, четверок и пятерок. (Обратите внимание, что формулу с функцией ЧАСТОТА нужно ввести только в четыре ячейки.)

Матричные операции Задание. Перейдите на новый рабочий лист и назовите его "Матрицы".

Простейшие операции, которые можно проделывать с матрицами: сложение (вычитание), умножение на число, перемножение, транспонирование, вычисление обратной матрицы.

Сложение матриц и умножение матрицы на число.

Задание. Сложить матрицы M и N, где

Ввести матрицы M и N в блоки А1 :С2 и Е1 :G2. В блок А4:С5 введем табличную формулу {= А1:С2 + E1:G2}.

Обратите внимание, что выделен блок, имеющий те же размеры, что и исходные матрицы.

Что произойдет, если перед вводом формулы выделить блок A4:D6? В "лишних" ячейках появится #Н/Д, т.е. "Недоступно".

Если выделить А4:В5, то будет выведена только часть матрицы, без каких-либо сообщений.

Использование имен делает процедуру ввода табличной формулы намного проще.

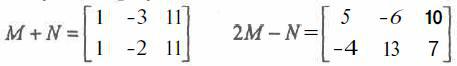
7

Задание. Дайте диапазонам А1:С2 и E1:G2 имена М и N. В блок E4:G5 введите табличную формулу {= М +N }. Результат, естественно, тот же.

Задание. Теперь вычислим линейную комбинацию матриц 2М - N. В блок А7:С8 введем табличную формулу {= 2*М — N }. Должны получиться

результаты

Рассмотренные примеры и упражнения показывают, что обычная

операция умножения применительно к блокам не вполне эквивалентна перемножению матриц.

И действительно, для матричных операций в Excel предусмотрены функции, входящие в категорию "Математические". Перечислим эти функции:

МОПРЕД — вычисление определителя матрицы; МОБР — вычисление обратной матрицы; МУМНОЖ— перемножение матриц; ТРАНСП — транспонирование.

Первая из этих функций возвращает число, поэтому вводится как обычная формула.

Задание. Перейдите на новый рабочий лист и назовите его "Матрицы

2".

Задание. Используя функцию МОПРЕД произвести расчёт векторного

произведения векторов

Остальные функции возвращают блок ячеек, поэтому они должны вводиться как табличные формулы. (Примеры, которые мы рассматривали

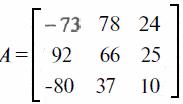
8

ранее, можно было выполнить и без использования табличных формул. Для матричных операций без табличных формул не обойтись.)

Первая буква "М" в названии трех функций — сокращение от слова "матрица".

Задание. Перейдите на новый рабочий лист и назовите его "Матрицы

3".

Задание. Вычислить определитель и обратную матрицу для матрицы

Проверить правильность вычисления обратной матрицы умножением ее на исходную. Повторить эти действия для той же матрицы, но с элементом азз= 10,01.

Разместим исходную матрицу в блоке А1 :СЗ. В ячейке В5 поместим формулу для вычисления определителя =МОПРЕД(А1 :СЗ).

В блок А7:С9 введем формулу для вычисления обратной матрицы. Для этого выделим блок А7:С9 (он имеет три строки и три столбца, как и исходная матрица). Введем формулу {=МОБР(А1:СЗ)}.

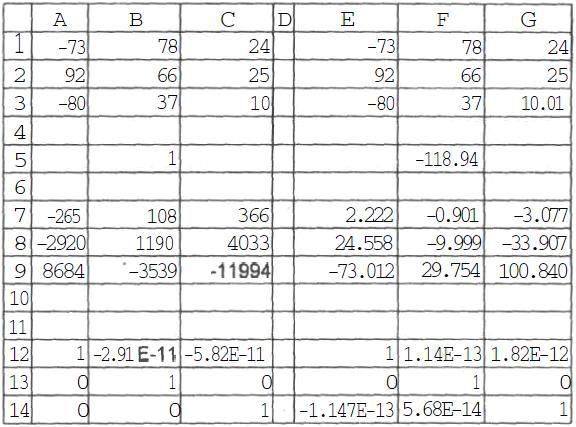
Скопируйте блок А1:С9 в блок E1:G9. Чуть-чуть изменим один элемент исходной матрицы: в ячейку G3 вместо 10 введите 10,01. Изменения в определителе и в обратной матрице значительны. Этот пример

иллюстрирует возможную численную неустойчивость вычисления определителя и обратной матрицы: малое возмущение на входе дает большое возмущение на выходе.

Для дальнейших вычислений присвоим матрицам на рабочем листе имена: А1:С3 — А, А7:С9 — Ainv, E1:G3 — АР, E7:G9 — APinv. Чтобы в уже введенных формулах появились эти имена, выберите в меню пункт "Вставка/ Имя/ Применить", выделите в диалоговом окне нужные имена и щелкните "ОК".

9

Теперь проверим правильность вычисления обратной матрицы. В блок А12:С14 введем формулу {=МУМНОЖ(Аж Ainv)}, а в блок E12:G14 -- формулу {=МУМНОЖ(АРж APinv)}. У Вас должен получиться результат

Как и следовало ожидать, получились матрицы, близкие к единичным.

Задание. В блоки I1:КЗ и I7:K9 введите табличные формулы (=abs(A- AP)} и {=abs(Ainv-APinv)}, чтобы посмотреть абсолютные отклонения величин в матрицах.

В матричных операциях можно использовать массив констант. Это матрицы, в которых элементы строк разделены точкой с запятой, а строки отделяются двоеточием. С частными случаями (вектор-строкой и вектор- столбцом) мы уже встречались. Вот пример вычисления определителя матрицы А, введенной в формулу как массив констант :

=МОПРЕД({ -73; 78; 24: 92; 66; 25: -80; 37; 10})

Задание. Даны матрицы

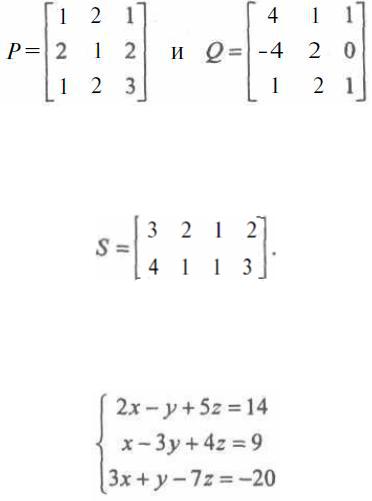
10

Вычислить определитель коммутатора этих матриц det(PQ – QP}. Все вычисления должны быть сосредоточены в одной ячейке.

Задание. Дана матрица

Вычислить матрицу 2SST - Е , где Т — операция транспонирования, Е

— единичная матрица.

Задание. Решить систему уравнений Ах = B по формуле х = А-1B.

Решение уравнений средствами Excel

1. Циклические ссылки

Задание. Создать лист Циклические ссылки

Если в ячейку Excel введена формула, содержащая ссылку на эту же самую ячейку (может быть и не напрямую, а опосредованно - через цепочку других ссылок), то говорят, что имеет место циклическая ссылка (цикл). На практике к циклическим ссылкам прибегают, когда речь идет о реализации итерационного процесса, вычислениях по рекуррентным соотношениям. В обычном режиме Excel обнаруживает цикл и выдает сообщение о возникшей ситуации, требуя ее устранения. Excel не может провести вычисления, так как циклические ссылки порождают бесконечное количество вычислений. Есть два выхода из этой ситуации: устранить циклические ссылки или