Двойственный симплексный метод

.

1. Решить задачу двойственным симплекс-методом.

Найдем псевдоплан задачи.

Решение системы линейных уравнений, определяемое базисом, называется псевдопланом задачи, если  для любого j.

Вводим дополнительные переменные , чтобы неравенства преобразовать в равенства (запишем в канонической форме):

В качестве базиса возьмем

Умножив все строки системы ограничений на -1, перейдем к задаче вида:

Решим эту систему относительно базисных переменных .

Полагая, что свободные переменные равны нулю, получаем первый опорный план:

Базис	В
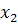
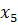
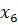
	-17	-7	-2	-3	1	0	0
	-13	-1	-4	-6	0	1	0
	-15	2	-1	-3	0	0	1
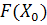
	0	-5	-7	-10	0	0	0

План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.

На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-7).

Базис	В
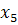
	-17	-7	-2	-3	1	0	0
	-13	-1	-4	-6	0	1	0
	-15	2	-1	-3	0	0	1
	0	-5	-7	-10	0	0	0
	-		3		-	-	-

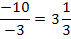
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.

Базис	В
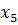
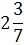
		1				0	0
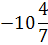
		0				1	0
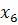
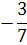
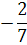
		0				0	1
		0				0	0

План 1 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец. На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный

Базис	В
		1				0	0
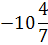
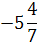
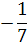
		0				1	0
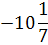
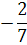
		0				0	1
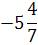
		0				0	0
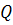
	0	-				-	-

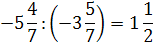
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.

Базис	В
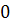
		1					0
		0					0
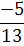
		0					1
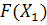
		0					0

План 2 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец. На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный

Базис	В
		1					0
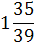
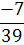
		0					0
		0					1
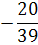
		0					0
	0	-	-	-

Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.

Базис	В
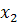
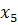
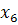
		1
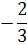
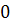
		0
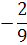
		0
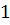
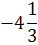
		0

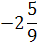
В базисном столбце все элементы положительные. Переходим к основному алгоритму симплекс-метода.

Индексная строка не содержит отрицательных элементов - найден оптимальный план. Это окончательный вариант симплекс-таблицы.

Оптимальный план можно записать так: