
- •Балтийский Федеральный Университет имени и. Канта
- •Расчетно-графическая работа №1
- •1.2 Статистический подход к измерению информации
- •Расчетно-графическая работа №2 Тема: «Разработка формальной грамматики Хомского».
- •1.1 Формальная грамматика
- •1.2 Пример построения грамматики
- •1.3 Представление грамматики в виде графа
- •1.5 Классификация формальных грамматик
- •Расчетно-графическая работа №3
- •Метод Шеннона-Фано
- •Метод Хаффмана
- •Расчетно-графическая работа №4 Тема: «Системы счисления».
- •Правила перевода целых чисел
- •Правила перевода правильных дробей
- •Правила сложения
- •Правила вычитания
- •Правила умножения
- •Правила деления
- •Расчетно-графическая работа №5 Тема: «Нормальные алгоритмы Маркова и машины Тьюринга».
- •Расчетно-графическая работа № 6 Тема: «Архивирование файлов алгоритмом Зива-Лемпеля-Велча».
- •7 Методические указания по выполнению расчетно-графической работы № 7 на тему: «Нахождение всех гамильтоновых циклов на ориентированном графе»
Метод Хаффмана
Этот метод имеет два преимущества по сравнению с методом Шеннона-Фано: он устраняет неоднозначность кодирования, возникающую из-за примерного равенства сумм частот при разделении списка на две части (линия деления проводится неоднозначно), и имеет, в общем случае, большую эффективность кода.
Исходное множество символов упорядочивается по не возрастанию частоты и выполняются следующие шаги:
1) объединение частот:
две последние частоты складываются, а соответствующие символы исключаются из списка;
оставшийся после исключения символов список пополняется суммой частот и вновь упорядочивается;
предыдущие шаги повторяются до тех пор, пока ни получится единица в результате суммирования и список ни уменьшится до одного символа;
2) построение кодового дерева:
строится двоичное кодовое дерево: корнем его является вершина, полученная в результате объединения частот, равная 1; листьями – исходные вершины; остальные вершины соответствуют либо суммарным, либо исходным частотам, причем для каждой вершины левая подчиненная вершина соответствует большему слагаемому, а правая – меньшему; ребра дерева связывают вершины-суммы с вершинами-слагаемыми. Структура дерева показывает, как происходило объединение частот;
ребра дерева кодируются: каждое левое кодируется единицей, каждое правое – нулем;
3) формирование кода: для получения кодов листьев (исходных кодируемых символов) продвигаются от корня к нужной вершине и «собирают» веса проходимых ребер.
Пример 2. Даны символы a, b, c, d с частотами fa = 0,5; fb = 0,25; fc = 0,125; fd= 0,125. Построить эффективный код методом Хаффмана.
объединение частот:
Таблица 3.2
|
Исходные символы s |
Частоты fs |
Этапы объединения | ||
|
первый |
второй |
третий | ||
|
|
0,5 |
0,5 |
0,5 |
1 |
|
|
0,25 |
0,25 |
0,5 |
|
|
|
0,125 |
0,25 |
|
|
|
d |
0,125 |
|
|
|
2) построение кодового дерева:



 1
1
1 0
0

 0,5a
0,5
0,5a
0,5
1

 0
0
 0,25
b
0,25
0,25
b
0,25
1
 0
0
0,125 c 0,125 d
3) формирование кода:
a - 1;
b - 01;
c - 001;
d - 000.
Как видно, полученные коды совпадают с теми, что были сформированы методом Шеннона-Фано, следовательно, они имеют одинаковую эффективность.
Примеры решения задач
Закодировать фамилию преподавателя методами Шеннона-Фано и Хаффмана.
Задание
Для выбранной в соответствии с вариантом задания задачи:
Закодировать сигнал методом Шеннона-Фано.
Закодировать сигнал методом Хаффмана.
Выполнить сравнительный анализ результатов кодирования.
Сделать выводы.
Содержание отчета
Подробное кодирование сигнала методом Шеннона-Фано, а именно:
таблица:
|
Символ алфавита А |
Число появлений mi |
Частота символа fi |
таблица:
|
Символ алфавита А |
Частота символа fi |
Этапы деления списка символов |
Результирующие коды |
двоичное дерево, изображающее деление списка частот символов;
коды фамилии, имени и отчества.
Подробное кодирование сигнала методом Хаффмана, а именно:
таблица:
|
Символ алфавита А |
Частота символа fi |
Этапы объединения частот |
кодовое бинарное дерево для метода Хаффмана,
таблицаСимвол
алфавита
Код
коды фамилии, имени и отчества.
Столбцы таблиц и таблицы должны быть пронумерованы.
Анализ результатов и выводы.
Варианты задания
Вариант задания формируется каждым студентом индивидуально следующим образом. От источника к приемнику передается следующее сообщение: «фамилия имя отчество». Каждый студент использует в качестве варианта задания свои фамилию, имя и отчество. Например: «иванов семен петрович».
Список литературы
Афанасьев В.В. Теория вероятностей в вопросах и задачах: http://cito-web.yspu.org/link1/metod/theory/theory.html
Топоркова О.М. Информатика: Учебн. пособ. – Калининград: КГТУ, 2001.
ЯгломА. М., ЯгломИ. М. Вероятность и информация. — М.: «Наука», 1973.

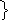
 a
a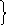
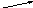 b
b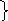
 c
c