линал билеты Крупин В.Г / билет 6
.docxМатрицы. Операции над ними. Определитель n-го порядка.
Матрицей размера m x n (читается m на n) называется прямоугольная таблица чисел, содержащая m строк и n столбцов.
Если у матрицы количество строк m совпадает с количеством столбцов n, то такая матрица называется квадратной, а число m=n называется размером квадратной матрицы или её порядком.
Диагональная матрица — квадратная матрица, все элементы которой кроме диагональных — нулевые.
Единичная матрица — матрица, при умножении на которую любая матрица (или вектор) остается неизменной, является диагональной матрицей с единичными (всеми) диагональными элементами

Нулевая матрица — матрица, все элементы которой нули (при сложении её с любой матрицей та остается неизменной, а при умножении на любую получается нулевая матрица).
Транспонированная матрица — матрица AT, полученная из исходной матрицы A заменой строк на столбцы.
Операции
Сложение матриц
Складывать можно только матрицы одинакового размера.
Сложение матриц A+B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.
Свойства сложения матриц:
коммутативность: A + B = B + A;
ассоциативность: (A + B) + C = A + (B + C);
сложение с нулевой матрицей: A + Θ = A;

Умножение матрицы на число
Умножение матрицы A на число λ заключается в построении матрицы λA = (λ*a_ij).
Свойства умножения матриц на число:
умножение на единицу: 1A = A;
ассоциативность: (λβ)A = λ(βA);
дистрибутивность: (λ + β)A = λA + βA, λ(A + B) = λA + λB;
Умножение матриц
Умножение матриц (обозначение: AB, реже со знаком умножения A x B) — есть операция вычисления матрицы C, каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.
Количество столбцов в матрице A должно совпадать с количеством строк в матрице B, иными словами, матрица A обязана быть согласованной с матрицей B. Если матрица A имеет размерность m x n, B — n x k, то размерность их произведения A B = C есть m x k.
Свойства умножения матриц:
ассоциативность: (AB)C = A(BC);
некоммутативность (в общем случае): AB != BA;
произведение коммутативно в случае умножения с единичной матрицей: AE = EA;
дистрибутивность: (A + B)C = AC + BC, A(B + C) = AB + AC;
ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB);
Определитель
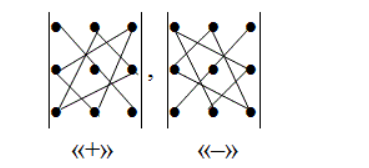
Определителем n-го порядка соответствующей квадратной матрице A n-го порядка называется сумма произведений элементов взятых из каждой строки каждого столбца по одному и умноженное на (-1)t, где t — чётность подстановки
Например,
при n = 6 произведение А21а13а62а34а46а55 является
членом определителя, так как в него
входит точно по одному элементу из
каждой строки и из каждого столбца.
Подстановка, составленная из его индексов
будет ![]() .
В ней 4-е инверсии в верхней строке и 2-е
инверсии – в нижней. Общее число инверсий
равно 6, т. е. подстановка чётная.
Следовательно, данное произведение
входит в разложение определителя со
знаком «+».
.
В ней 4-е инверсии в верхней строке и 2-е
инверсии – в нижней. Общее число инверсий
равно 6, т. е. подстановка чётная.
Следовательно, данное произведение
входит в разложение определителя со
знаком «+».
Определитель можно вычислить только для квадратной матрицы.
Для матрицы первого порядка значение определителя равно единственному элементу этой матрицы:

![]()
Определитель второго порядка равен разности произведений элементов главной диагонали и элементов побочной диагонали.
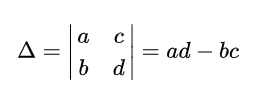
Определитель третьего порядка можно вычислить по формуле (правило треугольника)