Смешанное произведение трёх векторов.

При последовательном умножении трёх векторов 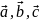могут представляться 3 случая:

1. 

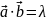
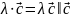
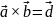
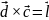2. - двойное векторное произведение.

Обозначение:

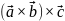
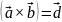
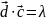3. - векторно-скалярное/ скалярно-векторное произведение.

Определение. Если два вектора умножают векторно , а полученный вектор 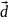скалярно умножают на вектор 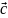, тогда такое произведение будет векторно-скалярным (смешанным).

Смешанным произведением будем называть число.

Обозначение:

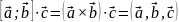
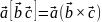
Пусть 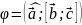. Тогда . .

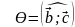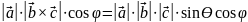Геометрический смысл.

Теорема. Смешанное произведение трёх векторов равно объёму параллелепипеда, построенного на этих векторах ( со знаком «+», если вектора образуют правую тройку, «-» - если левую).

Доказательство. . . .

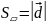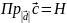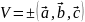Для любых векторов 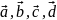и числа 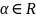имеют место следующие свойства:

1. ;

2. : ;

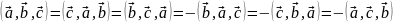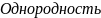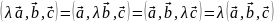3. Линейность:

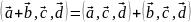
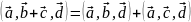
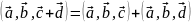
Доказательство. 1) В случае некомпланарных векторов доказательство вытекает из следующих утверждений: объём ориентированного параллелепипеда равен смешанному произведению образующих его векторов Ʌ при круговой перестановке образующих ориентированный параллелепипед некомпланарных векторов его объём не изменяется, а при перестановке двух- меняется только знак объёма. Вариант компланарных векторов является тривиальным, так как все указанные смешанные произведения равны 0 ( из условия компланарности 3-ёх векторов).

2) Из определения смешанного произведения и свойств скалярного имеем:

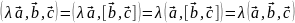
Учитывая п.1 и доказанное равенство далее получаем:

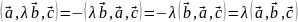
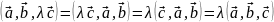
3) Опять же по определению смешанного произведения и свойствам скалярного получаем:

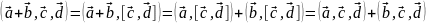
Остальные два равенства доказываются аналогично.

Найдём смешанное произведение в координатной форме:

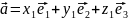
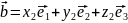
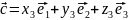
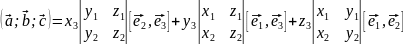
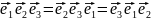
Учитывая знаки, имеем: