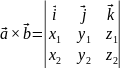линал билеты Крупин В.Г / билет 2
.docxВекторное произведение двух векторов.
Обозначение:
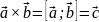
Векторным
произведением называется такой вектор
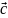 ,
который
удовлетворяет следующим условиям:
,
который
удовлетворяет следующим условиям:
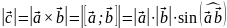
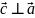 Ʌ
Ʌ
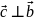 ,
то есть
,
то есть
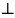 плоскости p,
в которой лежат
плоскости p,
в которой лежат
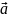 Ʌ
Ʌ
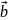 ;
;
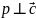
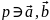
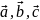 – образуют правую
тройку.
– образуют правую
тройку.
Модуль
с геометрической
точки зрения есть площадь параллелограмма,
построенного на
Ʌ
.
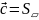
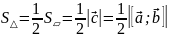
Свойства векторного произведения:
Обращается в ноль, когда хотя бы один из векторов =0 или векторы коллинеарны.
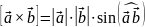 Если
Если
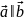 :
:
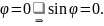 Критерий
коллинеарности:
Критерий
коллинеарности:
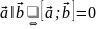 .
.
Доказательство:
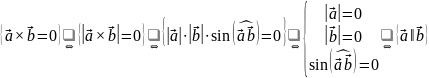
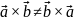 - не подчиняется
переместительному закону. Но если
- не подчиняется
переместительному закону. Но если
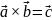 Ʌ
Ʌ
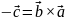 :
:
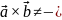
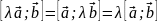 - сочетательный
закон относительно скалярного множителя.
- сочетательный
закон относительно скалярного множителя.
Доказательство:
Для
проверки справедливости этого свойства,
очевидно, достаточно показать, что
вектор
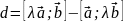 нулевой. Для этого убедимся, что
нулевой. Для этого убедимся, что
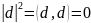 (используя определение смешанного
произведения и свойства скалярного).
(используя определение смешанного
произведения и свойства скалярного).
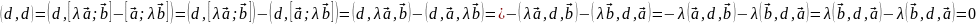 .
.
Аналогично
доказываем вторую часть данного свойства
(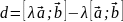 ).
).
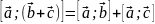 - распределительный
закон.
- распределительный
закон.
Векторное произведение векторов в координатной форме.
Пусть
задан произвольный базис
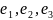 ,
тогда в этом базисе векторы имеют
разложение:
,
тогда в этом базисе векторы имеют
разложение:
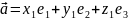
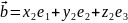
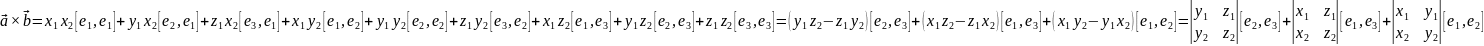 .
.
 ,
,
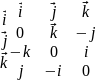 ,
,