Практика №4

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

УФИМСКИЙ УНИВЕРСИТЕТ НАУКИ И ТЕХНОЛОГИИ

Кафедра технической кибернетики

Задача динамического программирования

Вариант -24

Выполнил: студент гр. ИВТ-227б

Проверил: профессор каф. ТК

Гвоздев В.Е

Уфа 2023

Цель работы: ознакомиться с принципами и методами динамического программирования.

Задание: найти оптимальную траекторию для движения из точки А в точку В при заданных условиях.

Y

Вариант 24

A

16 15 14 13 12 11 10 9 8

8 9 10 11 12 13 14 15 16 17

10 14 8 10 14 10 8 14 10

7 8 9 10 11 12 13 14 15 15

12 8 13 10 9 12 11 13 10

11 14 13 12 11 10 9 8 7 14

10 10 13 15 10 12 11 14 8

8 6 5 6 7 8 9 10 11 13

12 9 11 10 9 14 10 13 12

9 12 13 14 15 16 17 16 15 12

X

8 9 12 15 13 15 15 13 16

11 14 13 12 11 10 9 8 7 10

B

12 8 13 10 9 12 11 13 10

Ход решения: Требуется проложить путь, соединяющий два пункта А и В. Допустим, что прокладка пути состоит из ряда шагов и на каждом шаге мы можем двигаться либо строго по Y, либо строго по X. Любой путь из А в В представляет собой ступенчатую ломаную линию, отрезки которой параллельны одной из координатных осей. Затраты на совершение каждого шага известны.

149

81

90

81

99

108

117

125

132

142

141

64

77

65

85

95

105

114

122

133

134

49

63

50

73

85

94

104

117

125

123

35

55

43

64

76

85

94

104

114

115

99

108

22

32

45

55

78

69

88

10

56

43

30

17

66

77

89

106

98

98

0

23

10

34

46

55

65

78

86

X=(c,c,c,c,c,в,в,в,c,в,в,в,в,в,в)

W=8+7+11+8+9+8+9+12+12+10+9+12+11+13+10=149

Теперь вернемся к началу и попробуем решить задачу «наивным» способом, выбирая на каждом шаге, начиная с первого, самое выгодное (для этого шага) направление (если таких два, выбираем любое). Таким способом мы получаем управление

(c,с,c,c,c,в,в,в,с,в,в,в,в,в,в )

Подсчитаем расходы для этой траектории. Они будут равны

W^*=8+7+11+8+9+8+9+12+12+10+9+12+11+13+10=149

Из полученных результатов можно сделать вывод, что решение наивным методом является оптимальным, так как W=W^*=149.

Контрольные вопросы:

1. Что такое «динамическое программирование»?

Динамическое программирование - особый метод оптимизации решений, специально приспособленный к так называемыми «многошаговыми» (или многоэтапными) операциями.

2. Что такое «операция» с точки зрения динамического программирования?

Операция   представляет собой управляемый процесс, т.е. мы можем выбирать какие-то параметры, влияющие на его ход и исход, причем на каждом шаге выбирается какое-то решение, от которого зависит выигрыш на данном шаге и выигрыш за операцию в целом.

3. Дайте содержательную трактовку понятию «оптимальное управление» с точки зрения динамического программирования.

Оптимальное управление – это такое управление, на каждом шаге которого выигрыш за всю операцию будет максимальным.

4. В чем заключается главный принцип динамического программирования?

Разбиение сложной задачи на множество простых и их решение. При этом не предполагается, что каждый шаг оптимизируется отдельно, независимо от других. Управление должно выбираться с учетом всех последствий в будущем.

5. В чем разница между условным оптимальным и оптимальным выигрышем?

Процесс динамического программирования обычно проходит от конца к началу: прежде всего планируется последний, m-й шаг. Учитывая, что, планируя последний шаг можно сделать разные предположения о том, чем закончится предпоследний (m-1)-й шаг, и для каждого из этих предположений найти условное оптимальное управление на m-м шаге («условное» потому, что оно выбирается из условия, что предпоследний шаг закончится так-то и так-то). Так, можно сказать, что разница оптимального и условно оптимального выигрыша в том, что условно оптимальный выигрыш получают на основе предположений о ток как закончится предыдущий шаг, а оптимальный выигрыш получают без оглядки на будущее.4

6. Дайте описание области применимости метода

Данный метод применяется для решения таких практических задач, в которых поиск оптимального решения требует поэтапного подхода, например в маршрутизаторах для реализации сетевых протоколов.

7. Сформулируйте и раскройте содержание практических рекомендаций, полезных при постановке задач динамического программирования.

1) Выбрать параметры (фазовые координаты), характеризующие состояние S управляемой системы перед каждым шагом.

2) Расчленить операцию на этапы (шаги).

3) Выяснить набор шаговых управлений   для каждого шага и налагаемые на них ограничения.

4. Определить, какой выигрыш приносит на   м шаге управление , если перед этим система была в состоянии S, то есть записать «функцию выигрыша»: 

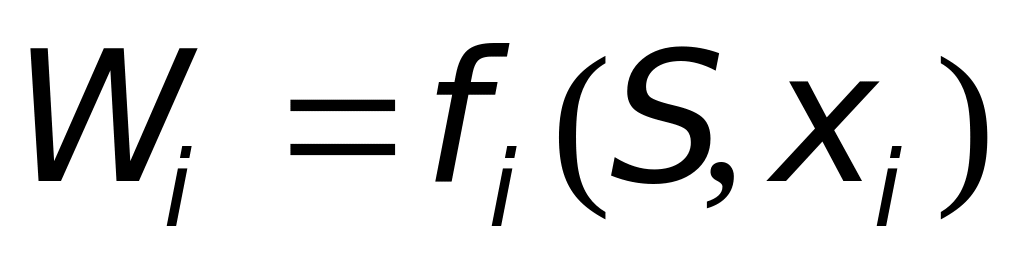
5. Определить, как изменяется состояние системы S под влиянием управления х_i на м шаге: оно переходит в новое состояние: 

6. Записать основное рекуррентное уравнение динамического программирования, выражающее условный оптимальный выигрыш   (начиная с го шага и до конца) через уже известную функцию   :   (4)

Этому выигрышу соответствует условное оптимальное управление на м шаге   (подчеркнем, что в уже известную функцию   надо вместо S подставить измененное состояние   .

7.Провести условную оптимизацию последнего m-го шага, задаваясь гаммой состояний S, из которых можно за один шаг дойти до конечного состояния, вычисляя для каждой из них условный оптимальный выигрыш по формуле: 

и находя условное оптимальное управление х_m(S), для которого этот максимум достигается.

8. Провести условную оптимизацию (m-1)-го, (m-2)-го и т.д. шагов по формуле (4), полагая в ней   =(m-1), (m-2), …, и для каждого из шагов указать условное оптимальное управление х_i(S), при котором этот максимум достигается.

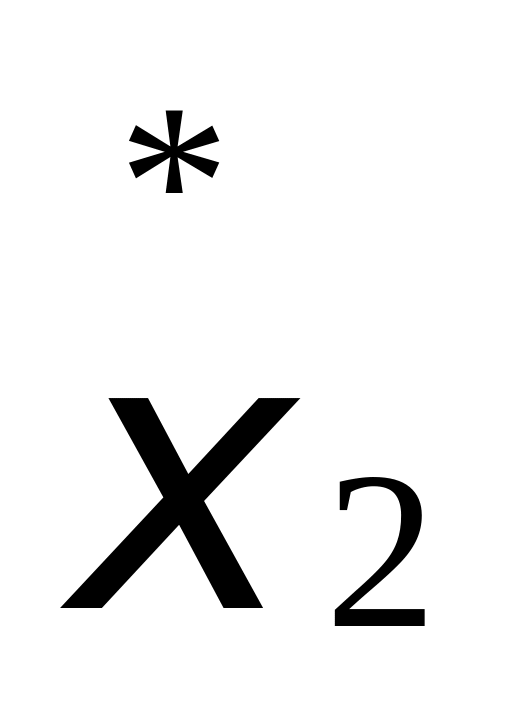9. Провести безусловную оптимизацию управления, «читая» соответствующие рекомендации на каждом шаге. Взять найденное оптимальное управление на первом шаге   =х₁(S₀). Изменить состояние системы по формуле (3); для вновь найденного состояния найти оптимальное управление на втором шаге   и.д. до конца.