
Практика №1
.doc
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
УФИМСКИЙ УНИВЕРСИТЕТ НАУКИ И ТЕХНОЛОГИИ
Кафедра технической кибернетики
Системы массового обслуживания
Методические указания по выполнению практической работы по дисциплине
«Моделирование»
Вариант -24
Выполнил: студент гр. ИВТ-227б
Проверил: профессор каф. ТК
Гвоздев В.Е
Уфа 2023
Задача: исследовать свойства n-канальной СМО с отказами, одноканальной СМО с неограниченной очередью и n-канальной СМО с неограниченной очередью.
n-канальная СМО с отказами.
Исходные данные:
Количество каналов (n): 5
Интенсивность потока заявок
(![]() ):
8
):
8
Среднее время обслуживания
(![]() ):
0.1
):
0.1
Требуется определить:
Финальные вероятности состояний;
Вероятность того, что поступившая заявка получит отказ;
Относительную пропускную способность СМО;
Абсолютную пропускную способность СМО;
Среднее число занятых каналов.
Решение:
![]()
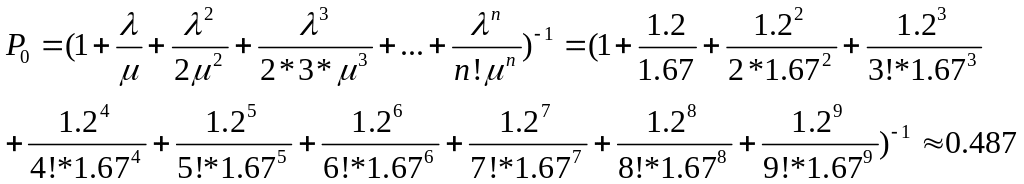
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -
относительная пропускная способность
-
относительная пропускная способность
![]() -
абсолютная пропускная способность
-
абсолютная пропускная способность
![]() -
среднее число занятых каналов
-
среднее число занятых каналов
Анализ результатов позволяет заключить, что СМО не перегружена: из 9-ти каналов занят в среднем один-два, а из поступающих заявок ни одна не остается необслуженной.
Одноканальная СМО с неограниченной очередью
Исходные данные:
Интенсивность потока заявок ( ): 8
Интенсивность обслуживания
заявок (![]() ):
8.5
):
8.5
Требуется определить:
Финальные вероятности состояний;
Среднее число заявок в системе;
Среднее время пребывания заявки в системе;
Среднее число заявок в очереди;
Среднее время пребывания заявки в очереди;
Степень загрузки канала.
![]() -
степень загрузки канала
-
степень загрузки канала
![]()
![]()
![]()
![]()
…
![]()
Lсист=![]() -
среднее число заявок в системе
-
среднее число заявок в системе
Wсист=![]() -
среднее время пребывания заявки в
системе
-
среднее время пребывания заявки в
системе
Lоч=![]() -
среднее число заявок в очереди
-
среднее число заявок в очереди
Wоч=![]() -
среднее время пребывания заявки в
очереди
-
среднее время пребывания заявки в
очереди
 -канальная
СМО с неограниченной очередью
-канальная
СМО с неограниченной очередью
Исходные данные:
Количество каналов (n): 6
Количество заявок (M): 3
Интенсивность потока заявок ( ): 0.3
Среднее время обслуживания ( ): 3
Требуется определить:
Оценить целесообразность замены одной n-канальной СМО с неограниченной очередью, предназначенной для обслуживания потока разнородных заявок, на совокупность n одноканальных СМО с неограниченной очередью, предназначенных для обслуживания однотипных заявок, при заданных характеристиках потоков заявок ( интенсивности заявок различных типов xi (i=1;m) полагается одинаковыми ).
Вариант I (существующий)
![]()
Так как ![]() <1,
финальные вероятности существуют.
<1,
финальные вероятности существуют.
 Lоч=
Lоч=![]()
Wоч=![]() Lоч=
Lоч=![]() (минут)
= 0.012 (секунд)
(минут)
= 0.012 (секунд)
Вариант II (предлагаемый)
![]()
![]()
Так как ![]() <1,
финальные вероятности существуют.
<1,
финальные вероятности существуют.
Lоч=![]() ;
;
Wоч=
Lоч=![]() (минут)
= 31,8 (секунд)
(минут)
= 31,8 (секунд)
Предлагаемый вариант не повысит эффективность обслуживания пассажиров.
Контрольные вопросы
Приведите примеры классификации систем массового обслуживания
Классификация по количеству каналов обслуживания: одноканальные и многоканальные.
По характеру обслуживания заявок: с отказами и с очередями.
СМО с очередями делятся на ограниченные и неограниченные.
СМО с ограниченными очередями по дисциплине обслуживания делятся на обслуживающие в случайном порядке, порядке поступления и приоритетном порядке (последние делятся на абсолютные и относительные)
Какой содержательный смысл имеет понятие «финальная вероятность состояния»?
Финальную вероятность состояния можно понимать как вероятность того, что в случайный момент времени СМО окажется в определенном состоянии.
В чем заключается содержательный смысл формулы Литтла?
Формула Литтла устанавливает, что среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок.
Перечислите и дайте содержательное толкование основных характеристик эффективности СМО.
Среднее число заявок в СМО — это средняя разница между пребывшими в СМО и покинувшими СМО заявками.
Среднее время пребывания заявки в СМО — это среднее время, в течение которого заявка обслуживается.
Относительная пропускная способность – вероятность того, что заявка будет обслужена.
Абсолютная пропускная способность - среднее число заявок, обслуживаемых в единицу времени.
Вероятность отказа - вероятность того, что заявка покинет СМО необслуженной.
Среднее число занятых каналов.
Среднее число заявок в очереди — это средняя разница между пребывшими в СМО и покинувшими очередь заявками.
Среднее время пребывания заявки в очереди — это среднее время между прибытием заявки в очередь и началом ее обслуживания.
Степень загрузки канала - вероятность того, что канал занят.
Какой содержательный смысл имеет приведенная интенсивности потока заявок?
Смысл приведенной интенсивности потока заявок - среднее число заявок, приходящее за среднее время обслуживания одной заявки.
Почему для одноканальной СМО с неограниченной очередью значение относительной пропускной способности равно единице?
Относительная пропускная способность — это вероятность того, что заявка будет обслужена. Так как очередь неограниченна, каждая заявка когда-либо будет обслужена, а значит, вероятность ее обслуживания равна 1.
Каковы особенности анализа одноканальных СМО с неограниченной очередью
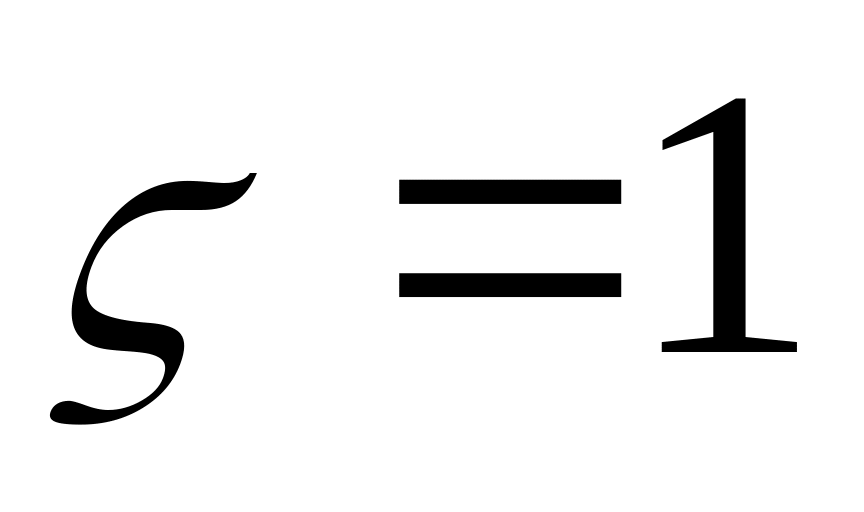 ?
?
В этом случае СМО справляется с потоком заявок, только если поток этот – регулярен, и время обслуживания - тоже не случайное, равное интервалу между заявками. В этом «идеальном» случае очереди в СМО вообще не будет, канал будет непрерывно занят, и будет регулярно выпускать обслуженные заявки. Но стоит только потоку заявок или потоку обслуживания стать случайным, очередь будет расти до бесконечности.
Почему в одноканальных СМО с неограниченной очередью при
 <1
наиболее вероятное число заявок в
системе равно нулю?
<1
наиболее вероятное число заявок в
системе равно нулю?
При ![]() <1
за время обслуживания одной заявки
приходит меньше одной новой заявки, то
есть канал не всегда занят. Поэтому
вероятность того, что он свободен, выше
того, что он занят.
<1
за время обслуживания одной заявки
приходит меньше одной новой заявки, то
есть канал не всегда занят. Поэтому
вероятность того, что он свободен, выше
того, что он занят.
Приведите содержательные примеры сравнительного анализа эффективности n-канальных и совокупности n-одноканальных СМО с неограниченной очередью.
Из-за случайного характера поступления заявок в совокупности n-одноканальных СМО могут быть состояния системы, когда обращения производятся к СМО, которая занята, при наличии свободных СМО. При одной многоканальной СМО такого состояния быть не может. Из-за этого эффективность одной многоканальной СМО всегда выше нескольких одноканальных.
10. Дайте описание областей применимости изученных моделей.
Такие модели используются в областях, в которые в поступают заявки на обслуживание и эти заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания.
