
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Юго-западный государственный университет»
Факультет фундаментальной и прикладной информатики
Кафедра «Информационная безопасность»
Предмет «Математическая логика и теория алгоритмов»
Лабораторная работа № 4
Вариант 5
Исполнитель:
студент группы ИБ-11б
Гребенникова А.И.
Проверяющий:
профессор, д.физ-мат.н.
Добрица В.П.
Курск 2022
Цель: изучить понятия высказывания, формулы, подформулы, сложность формулы, типы формул, эквивалентные формулы и эквивалентные преобразования формул.
Задача 1. Среди данного набора функций указать а) монотонные, б)
самодвойственные, в) линейные, г) сохраняющие 0, д) сохраняющие 1.
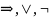
А) Булева функция называется монотонной, если тождественно истинна импликация: (α1 , … , αn) ≼ (β1 , … , βn)f (α1 , … , αn) ≤ f (β1 , … , βn), иначе говоря, функция принадлежит классу монотонных функций (M), если для любой пары наборов α и β таких, что α ≤ β, выполняется условие f(α) ≤ f(β).
Среди данных ф-й монотонных нет.
(Как определяется порядок ≼? Свой вывод обоснуйте в соответствии с определением.)
Две последовательности из 0 и 1 α1, …, αn и (β1, …, βn) назовем соседними, если существует единственная координата i, что αi < βi и для всех j ≠ i выполняются равенства αj = βj .
(Это определение соседних наборов, но не порядка!)
(α1 , … , αn) ≼ (β1 , … , βn), если для каждого i ∈ (1,2, … , n) выполняется неравенство αi ≤ βi
Функция
Сравниваем соседние наборы по 1-й переменной:
Сравним значения {1} и {1}: условие монотонности выполнено.
Сравним значения {0} и {1}: условие монотонности выполнено.
Сравниваем соседние наборы по 2-й переменной:
Сравним значения {0,0} и {1,0}: условие монотонности нарушено.
Таким образом функция не принадлежит классу M.
(А почему не по определению дествуете?)
Данные рассуждения я провела по определению, сравнив соседние аргументы и значение функции на этих наборах.
X |
Y |
X→Y |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
Сначала мы сравниваем наборы на 4 и 2 строках, т.е. {1} и {1}: условие монотонности выполнено; {0} и {1}: условие монотонности выполнено.
Аналогично сравниваем наборы на 1 и 3 строках, на них условие монотонности нарушено.
(Но для проверки монотонности надо пользоваться определением монотонности, в котором используется порядок на последовательностях из 0 и 1.)
При выполнении проверки монотонности я так же учитываю порядок на последовательностях, т.е. сравниваю аргументы строго по неравенству xi≤yi.
Функция
Функция принадлежит классу монотонных функций M, если для любой пары наборов α и β таких, что α ≤ β, выполняется условие f(α) ≤ f(β).
(0,0) = 1 и (0,1) = 1 - монотонность не нарушена.
(0,0) = 1 и (1,0) = 1 - монотонность не нарушена.
(0,1) = 1 и (1,1) = 0 - монотонность нарушена. Значит функция не принадлежит классу монотонных функций M.
(Как может пара равняться числу?)
Пара – это значения переменных, т.е. данная запись означает
f(0, 1) = 1 (Вот так и надо записывать!)
или
При X=0, Y=1 значение функции X→Y f=1.
X |
Y |
X|Y |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Функция
Функция принадлежит классу монотонных функций (M), если для любой пары наборов α и β таких, что α ≤ β, выполняется условие f(α) ≤ f(β).
Сравниваем соседние наборы по 1-й переменной: (А здесь сколько аргументов?) 1 переменная X
X |
¬X |
0 |
1 |
1 |
0 |
Сравним значения {1} и {0}: условие монотонности нарушено.
Таким образом функция не принадлежит классу M.
Б) Функция f называется самодвойственной, если она двойственна сама себе, т.е. выполняется равенство f∗ (x1 , ⋯ , xn) = f(x1 , ⋯ , xn).
Из данных ф-й самодвойственной является
(Дайте необходимые определения и ответ обоснуйте.)
Булева функция f*(x1, …, xn) называется двойственной булевой функции f(x1, …, xn), если она получена из f(x1, …, xn) инверсией всех аргументов и самой функции, то есть
f*(x1,
…, xn)
=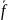 (
(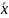 1,
…,
n).
1,
…,
n).
Если функция на противоположных наборах принимает противоположные значения, то она принадлежит классу самодвойственных функций S.
X |
Y |
X→Y |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
Проверим значения на наборах {0, 0} и {1, 1}: 1 и 1 совпадают.
Поэтому функция не принадлежит классу S.
X |
Y |
X|Y |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Проверим значения на наборах {0, 0} и {1, 1}: 1 и 0 противоположны
Проверим значения на наборах {0, 1} и {1, 1}: 1 и 1 совпадают.
Поэтому функция не принадлежит классу S
x |
¬X |
0 |
1 |
1 |
0 |
Проверим значения на наборах {0, 0} и {1, 1}: 1 и 0 противоположны. Поэтому функция принадлежит классу S (А сколько аргументов у этой функции? Распишите в точном соответствии с определением.)
Один аргумент х. Таблица истинности этой функции удовлетворяет условию самодвойственности (функция на противоположных наборах принимает противоположные значения) и столбец ее значений переходит сам в себя при инвертировании. В нашем случае, функция является самодвойственной.
В) Булева функция f(x1 , … , xn) называется линейной, если ей эквивалентный полином Жегалкина имеет первую степень
![]()
Из данных ф-й линейными являются и (Даже по Ваши дальнейшим рассуждениям это не так!)
Из данных ф-й линейной является ф-я .
(Дайте определения алгебры Жегалкина и полиномов Жегалкина. Свой вывод обоснуйте.)
Алгебра Жегалкина - множество булевых функций, рассматриваемое вместе с операциями конъюнкции и сложения (по модулю два).
Полиномы Жегалкина играю роль совершенных нормальных форм булевой алгебры в алгебре Жегалкина. (А что же это такое?)
Сумма по модулю 2 произведений переменных и, быть может,
