Г л. в. Измерение акустических сопротивлений

Начало биполярной системы определяется по этим точкам следующим образом: определим l_s как длину трубы, при которой значения Хет и Ret дают точку, лежащую дальше всех других точек на биполярной оси х (см. фиг. 204). Затем, увеличивая и уменьшая длину трубы на Х/8, най- дем точки Р U_s — Х/8] и Р [Z_s + Х/8]. Пересечение касательных к окружности в этих точках и определяет начало координат биполярной системы. Задача сводится, таким образом, к нахождению точки Р (l_s) по графику фиг. 204.

Фэй показал [30], что все хорды, проходящие через любые две точки окружности, для которых длины трубы различаются на Х/4, проходят

через одну точку, лежащую на оси х. Следовательно, прямая, про- ходящая через эту точку и через центр окружности, даст искомую ось гг. Значение I для точки, лежа- щей на этой оси и наиболее уда- ленной от начала координат бипо- лярной системы, равно l_s. Зна- чение X получается из (6.47) де- лением правой части равенства на частоту звука. Скорость с в сво- бодном воздухе при различных температурах указана в гл. 1.

Диаметры двух окружностей, получаемых при двух длинах тру- бы, закрываемой жестким порш- нем, несколько различаются между

собой вследствие наличия поглощения на стенках трубы. Для полу- чения поправки на это поглощение и приходится строить несколько

окружностей.

Из уравнения (6.81) и фиг. 204 видно, что сопротивление А соответ- ствует пересечению осей жиуи что окружность внесенного сопротивления, отнесепная к этой точке на плоскости Хет, Ret, дается уравнением

— В th [(Фа + фо) +1 (?а сро)] • (6.82)

Пусть теперь радиус окружности на фиг. 204 равен г в омах и пусть

б — угол радиус-вектора какой-либо точки Р (I) с осью х. Тогда можно показать, что

(6.83)

(6.84)

где Z_s —длина столба воздуха, соответствующая 0 = 0, и

sh 2 (<jj_A + <Ы = — - , (6.85а)

откуда

ф_А = 4" arcsh(^^ — ф₀- (6.856)

Для примера рассмотрим таблицу типичных данных измерения (табл. 19, фиг. 205). Значения | В | рассчитываются по (6.83) и (6.84); используются средние величины для многих различных длин I. Величина фл + ф₀ ^П0ЛУ“ чается непосредственно из (6.856). Значение а, входящее в таблицу, задается в непер I см. Ясно, что по трем группам данных мы получим зна­чения фз = (фд — aAZ_s) — величину, относящуюся к самому образцу.

I J9| =

9 =

г sin 2ср

tgfl

2* (l — l_s)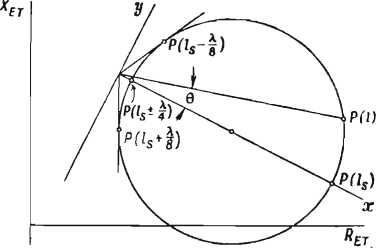

Фиг. 204. Диаграмма внесенного сопро- тивления, полученная методом «реакции на источник» [23].

15*

_1 —-°т L

/5 20 25 30

Ret

228

Г л. 6. Измерение акустических сопротивлений

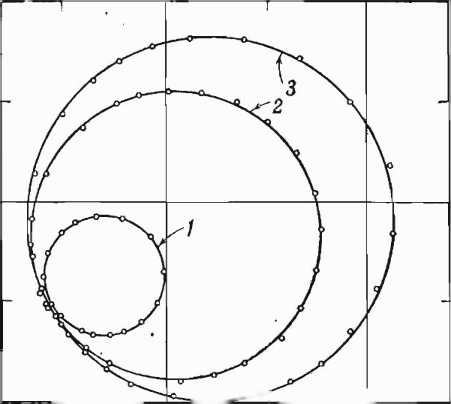
сопротивления Z_P достаточно мала. В этом излучателе подвижная катушка непосредственно приводит в движение алюминиевый поршень, подвешен­ный на радиально натянутых проволоках, эффективная длина которых может регулироваться. Поршень помещается в трубу; уплотнение зазора между поршнем и стенками трубы не может быть осуществлено ввиду сравнительно большого затухания, вызываемого уплотнением. Поэтому приходится отдельно учитывать поправку на утечку звуковой энергии через зазор. Авторы указывают на практическую применимость устрой­ства, но отмечают трудности, связанные с чрезвычайно острой настройкой.

Б. Измерение изменения звукового давления. Фландерс [24] пред­ложил метод непосредственного измерения сопротивления с помощью двух других известных сопротивлений; измерение требует трех отсчетов на электрическом потенциометре, соответствующих балансу. Схема устройства приведена на фиг. 206¹).

Акустический щуп измеряет давление на плоскости а—а, соединяю­щей измерительный прибор с акустическим сопротивлением Z. Если ток через телефон равен нулю, то ток, проходящий через сопротивление г и первичную обмотку индуктивной связи т, пропорционален давлению, измеряемому микрофоном в а —а. Ток I создает напряжение Е' на вторич­ной обмотке ш и на сопротивлении г. Обычно измерения начинаются <с помещения в а —а бесконечного сопротивления (жесткий поршень). Затем, изменяя гит, добиваются баланса. При этом тоК I оказывается пропорциональным «давлению р₂ в разомкнутой цепи в точке а — аъ. Иначе говоря, согласно теореме Тевенена, звуковое давление, измеряемое яа клеммах а —а, равно «давлению разомкнутой цепи» акустического гене­ратора. Если затем последовательно помещать в а —а два сопротивления SjhZ, то, обозначая через z_s внутреннее акустическое сопротивление изме­рительной установки в сторону громкоговорителя, получим

я

Pi

Pz^zi

PzZ

Z + z_s *

Исключая отсюда z₈, найдем

Z

ч

P2

Pi

-1

P 2 Pb

(6.88)

(6.89)

(6.90)

Контрольное напряжение Е₀ остается для всех трех случаев одинаковым и равным Е' при балансе. Следовательно, г-\-/ыт должно быть обратно пропорционально /, а также и р. Уравнение (6.90) принимает тогда вид

Ч ~ (^гз — г₂) + /а>(т₃ — т₂)^ ■ \ - )

На практике в качестве z_a выбирают входное сопротивление закры­той трубы с жесткими стенками длиной Х/8; тогда = — /рс. Дальнейшее упрощение расчета достигается, если взять т₂ = 0 для случая бесконеч­ного сопротивления. Для этого при помещении в а — а жесткого поршня обращают т в нуль, а г берут в районе средней части шкалы; затем доби­ваются баланса, соответственно регулируя М' иR'. Полученные значения