- •Введение
- •1 Проектирование рельсовой колеи
- •1.1 Рельсовая колея на прямых участках
- •1.2 Особенности устройства рельсовой колеи в кривых участках
- •1.3 Расчет возвышения наружного рельса в кривом участке пути
- •1.4 Проектирование переходных кривых
- •1.5 Расчет количества и порядка укладки укороченных рельсов на внутренней нити кривой
- •1.6 Расчет увеличения междупутного расстояния в кривых
- •1.7 Выводы по первому разделу
- •2 Расчет и проектирование одиночного обыкновенного стрелочного перевода
- •2.1 Принципиальная схема обыкновенного стрелочного перевода
- •2.2 Расчетная геометрическая схема обыкновенного стрелочного перевода
- •2.3 Основные параметры стрелки
- •2.3.1 Начальный стрелочный угол, радиусы остряка и переводной кривой, полный стрелочный угол
- •2.3.2 Длина криволинейного остряка и рамных рельсов
- •2.4 Геометрические характеристики крестовины
- •2.4.1 Угол крестовины и длина прямой вставки перед ее математическим центром
- •2.4.2 Минимальная длина сборной крестовины с литым сердечником
- •2.5 Определение основных параметров стрелочного перевода
- •2.6 Ординаты для разбивки переводной кривой
- •2.7 Установление ширины колеи
- •2.8 Определение длин рельсовых нитей стрелочного перевода
- •2.9 Раскрой рельсовых нитей на соединительных путях стрелочного перевода
- •2.10 Компоновка эпюры обыкновенного одиночно стрелочного перевода
- •2.11 Основные требования правил технической эксплуатации к содержанию стрелочных переводов
- •2.12 Проектирование съезда
- •2.13 Выводы по второму разделу
- •Заключение
- •Список использованных источников
1.4 Проектирование переходных кривых
Прямые и круговые кривые во избежание внезапного появления центробежной силы должны сопрягаться плавно с помощью переходных кривых. Основное назначение переходных кривых заключается в обеспечении плавного изменения центробежных сил при выходе экипажа в переходную кривую и выходе из нее. На их протяжении осуществляют плавные отводы возвышения наружной рельсовой нити и уширения колеи в круговой кривой.
В
качестве переходных кривых чаще всего
используют радиоидальные спирали. У
этих кривых кривизна
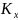 изменяется прямопропорционально длине
изменяется прямопропорционально длине
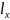
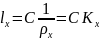 , (1.14)
, (1.14)
где
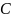 – коэффициент пропорциональности –
параметр переходной кривой;
– коэффициент пропорциональности –
параметр переходной кривой;
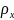 – радиус кривизны.
– радиус кривизны.
Длина
переходной кривой
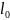 определяется из условий ограничения
вертикальных составляющих скорости
подвижного состава по переходной кривой
[6]
определяется из условий ограничения
вертикальных составляющих скорости
подвижного состава по переходной кривой
[6]
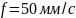 ,
,
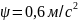 .
.
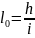 , (1.15)
, (1.15)
где
 –
рекомендуемый уклон отвода возвышения
–
рекомендуемый уклон отвода возвышения
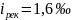 .
.
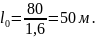
По второму условию, ограничения скорости нарастания непогашенного горизонтального ускорения
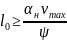 , (1.16)
, (1.16)
при
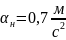
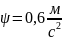 .
.
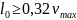 . (1.17)
. (1.17)
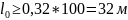 .
.
Значения
переходной кривой округляется до
значения кратному 10 м в большую сторону.
Для дальнейших расчетов принимается
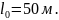
Учитывая,
что для конца переходной кривой
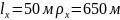 параметр переходной кривой определяется
как
параметр переходной кривой определяется
как
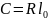 , (1.18)
, (1.18)
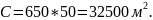
Разбивка переходной кривой осуществляется на местности со сдвижкой ранее размеченной кривой на величину p (рисунок 1.4), которая определяется по формуле
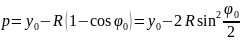 , (1.19)
, (1.19)
где p – сдвижка круговой
кривой внутрь;
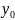 – координата конца переходной кривой;
– координата конца переходной кривой;
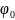 – угол поворота на протяжении переходной
кривой.
– угол поворота на протяжении переходной
кривой.
Угол поворота
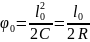 , (1.20)
, (1.20)
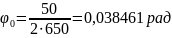 .
.
Возможность разбивки переходной кривой определяется следующими условиями
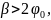
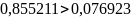 – условие выполняется.
– условие выполняется.
Длина
круговой кривой должна быть не менее
30 м
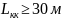 .
.
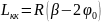 , (1.21)
, (1.21)
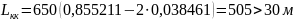 – условие выполняется.
– условие выполняется.
Для осуществления разбивки переходной кривой необходимо определить ее вид.

Рисунок 1.4 – схема разбивки переходной кривой.
Вид кубической параболы принимается при условии
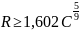 , (1.22)
, (1.22)
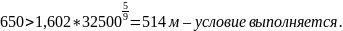
При кубической параболе координаты кривой определяются по формуле
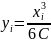 , (1.23)
, (1.23)
где
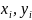 – координаты точек переходной кривой.
– координаты точек переходной кривой.
Расчет координат переходной кривой ведется в табличной форме (таблица 1.3).
Таблица 1.3 – Координаты переходной кривой по кубической параболе.
-
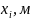
0
10
20
30
40
50
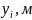
0
0,005
0,041
0,138
0,328
0,641
По результатам расчетов в таблице 1.3 строится график переходной кривой (рисунок 1.5)
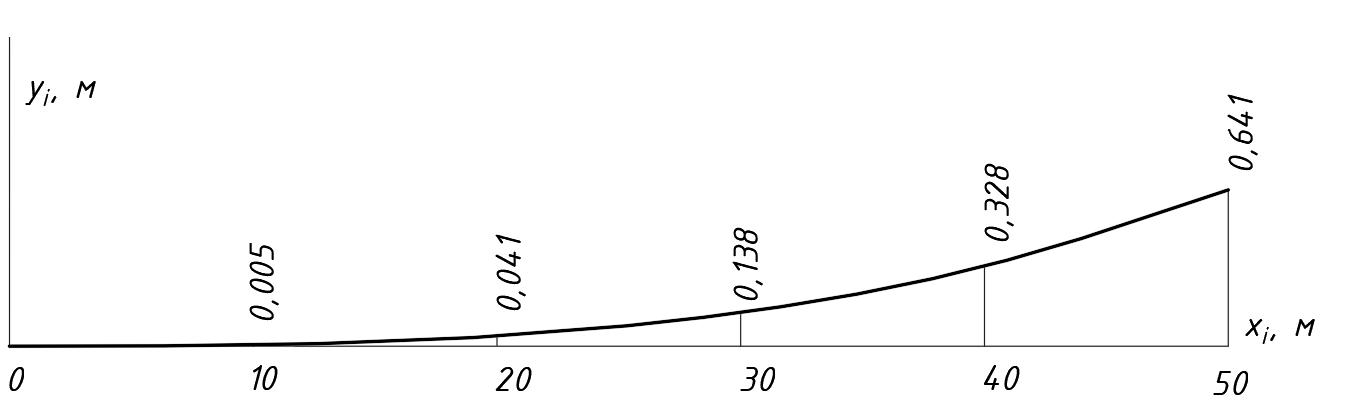
Рисунок 1.5 – График переходной кривой.
Тогда сдвижка круговой кривой вовнутрь составит
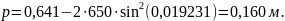
Расстояние m от начала переходной кривой до отнесенного тангенсного столбика находится по формуле
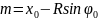 , (1.24)
, (1.24)
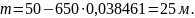
Расстояние
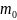 от начала переходной кривой до
первоначального тангенсного столбика
определяется по формуле
от начала переходной кривой до
первоначального тангенсного столбика
определяется по формуле
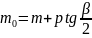 . (1.25)
. (1.25)
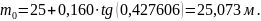
Полная длина кривой с учетом переходных кривых определяется по формуле
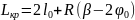 , (1.26)
, (1.26)
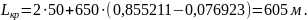
Суммарный тангенс кривой определяется по формуле
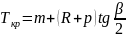 , (1.27)
, (1.27)
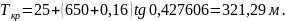
Суммарная биссектриса определяется по формуле
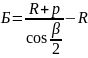 , (1.28)
, (1.28)
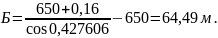
Домер рассчитывается по формуле
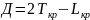 , (1.29)
, (1.29)