
- •Contents
- •Series Preface
- •Introduction
- •Floating-Point Numbers
- •Computational Cost
- •Fidelity
- •Code Development
- •List of Open-Source Tools
- •Exercises
- •References
- •Derivation of the Wave Equation
- •Introduction
- •General Properties of Waves
- •One-Dimensional Waves on a String
- •Waves in Elastic Solids
- •Waves in Ideal Fluids
- •Thin Rods and Plates
- •Phonons
- •Tensors Lite
- •Exercises
- •References
- •Methods for solving the Wave Equation
- •Introduction
- •Method of Characteristics
- •Separation of Variables
- •Homogeneous Solution in Separable Coordinates
- •Boundary Conditions
- •Representing Functions with the Homogeneous Solutions
- •Green
- •Method of Images
- •Comparison of Modes to Images
- •Exercises
- •References
- •Wave Propagation
- •Introduction
- •Fourier Decomposition and Synthesis
- •Dispersion
- •Transmission and Reflection
- •Attenuation
- •Exercises
- •References
- •Normal Modes
- •Introduction
- •Mode Theory
- •Profile Models
- •Analytic Examples
- •Perturbation Theory
- •Multidimensional Problems and Degeneracy
- •Numerical Approach to Modes
- •Coupled Modes and the Pekeris Waveguide
- •Exercises
- •References
- •Ray Theory
- •Introduction
- •High Frequency Expansion of the Wave Equation
- •Amplitude
- •Ray Path Integrals
- •Building a Field from Rays
- •Numerical Approach to Ray Tracing
- •Complete Paraxial Ray Trace
- •Implementation Notes
- •Gaussian Beam Tracing
- •Exercises
- •References
- •Introduction
- •Finite Difference
- •Time Domain
- •FDTD Representation of the Linear Wave Equation
- •Exercises
- •References
- •Parabolic Equation
- •Introduction
- •The Paraxial Approximation
- •Operator Factoring
- •Pauli Spin Matrices
- •Reduction of Order
- •Numerical Approach
- •Exercises
- •References
- •Finite Element Method
- •Introduction
- •The Finite Element Technique
- •Discretization of the Domain
- •Defining Basis Elements
- •Expressing the Helmholtz Equation in the FEM Basis
- •Numerical Integration over Triangular and Tetrahedral Domains
- •Implementation Notes
- •Exercises
- •References
- •Boundary Element Method
- •Introduction
- •The Boundary Integral Equations
- •Discretization of the BIE
- •Basis Elements and Test Functions
- •Coupling Integrals
- •Scattering from Closed Surfaces
- •Implementation Notes
- •Comments on Additional Techniques
- •Exercises
- •References
- •Index
6
Normal Modes
6.1 Introduction
In many practical situations, the refractive properties of the medium depend on one coordinate. In such cases the wave equation can be separated in a suitable coordinate system, and the solution described by a factor that represents a propagating wave in two dimensions and time and a factor that is a solution to a one-dimensional ordinary differential equation containing the index of refraction. This equation is similar in form to Schrödinger’s time-independent eigenvalue equation for the wave function of a particle in a potential well. The set of solutions to this equation are referred to as normal modes and can be used to build up a complete solution to the acoustic wave equation for a collection of point sources embedded in the medium. Due to the nature of the potential well and possible boundary conditions, the spectrum of these modes may be continuous or discrete. There exist a handful of example refractive index functions for which exact solutions to this equation may be found in terms of special functions. More general cases require approximation or numerical methods. This chapter introduces normal mode theory applied to the second-order wave equation for the pressure field with a depth-dependent refractive index. Some cases leading to exact solutions are presented to illustrate the general features of the modes. To solve more complex problems, this chapter presents perturbation theory and applies it to several problems with boundary conditions. Afterward the relaxation technique is presented and discussed as a numerical method for solving the eigenvalue problem with boundary conditions and nontrivial refractive index. The final section contains a brief description of the theory behind coupled modes and their use in extending mode theory to more general environments.

6.2 Mode Theory
Consider an environment described by c = c z
z , υ0 = 0, and ρ0 = constant. The pressure field obeys the wave equation (6.1):
, υ0 = 0, and ρ0 = constant. The pressure field obeys the wave equation (6.1):
2p− |
1 ∂2p |
= 0 |
(6.1) |
||||||
c |
2 |
∂t |
2 |
|
|||||
|
|
|
|
|
|
||||
Assuming time harmonic behavior, p = φ x |
|
exp − iωt , for the pressure field, |
(6.1) is |
||||||
converted into the Helmholtz equation for φ x |
: |
|
|
|
|||||
2φ + |
ω2 |
φ = 0 |
(6.2) |
||||||
c2 |
|||||||||
|
|
|
|
|
|
|
|||
Applying separation of variables in x , φ x
x = X
= X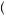 x
x Y
Y y
y Z
Z z
z , leads to a set of ordinary differential equations (ODE) for each factor:
, leads to a set of ordinary differential equations (ODE) for each factor:
|
X |
= − k2X |
|
(6.3) |
||
|
|
|
|
x |
|
|
|
Y |
= − k2Y |
|
(6.4) |
||
|
|
|
|
y |
|
|
|
ω2 |
− k2 |
Z = 0 |
(6.5) |
||
Z |
+ |
|
|
|||
|
|
|||||
|
|
|
c2 |
T |
|
|
|
|
|
|
|
|
|
The separation constants kx2 and ky2 have been introduced, having the physical interpretation of wavevector components in the x and y directions, respectively. The transverse wavenumber, kT =  kx ky 0
kx ky 0 T , kT2
T , kT2  kx2 + ky2, appears in (6.5). The solution for the transverse propagation is given by a plane wave:
kx2 + ky2, appears in (6.5). The solution for the transverse propagation is given by a plane wave:
XY = exp ikT x |
(6.6) |
When c = constant, the term in brackets in (6.5) is identified as the wavenumber kz2, and the separation constants obey the dispersion relation
k2 |
+ k2 |
+ k2 |
= |
ω2 |
(6.7) |
|
|||||
x |
y |
z |
|
c2 |
|
|
|
|
|
|
A complete solution is a plane wave traveling in the k direction. In the general case a position-dependent wavenumber is defined:
k2 |
ω2 |
− k2 |
(6.8) |
|
|||
z |
c2 |
T |
|
|
|
|

With this definition (6.5) is written in compact form:
d2Z |
+ k2 |
z Z = 0 |
(6.9) |
|
|||
dz2 |
z |
|
|
|
|
|
Solutions to (6.9) may have bound (decaying) or unbound (oscillatory) behavior depending on the sign of kz2. Since this is no longer constant, there may be locations where the behavior changes from one type to the other. The zeros of kz2 will be determined by the specific nature of the sound speed function c(z). Consider a single transition point at some arbitrary value, z = z , for which kz2
, for which kz2 z
z = 0. From (6.9) it follows that this is a point of inflection of the function Z. For values of z such that kz2 > 0, the solution will have oscillatory behavior, and for kz2 < 0 it will have exponential behavior.
= 0. From (6.9) it follows that this is a point of inflection of the function Z. For values of z such that kz2 > 0, the solution will have oscillatory behavior, and for kz2 < 0 it will have exponential behavior.
6.3 Profile Models
Physical models of refraction in underwater acoustics frequently involve mathematical models of speed profiles that tend to infinity at  z
z
 ∞. Simple models with this behavior include the following:
∞. Simple models with this behavior include the following:
c z |
= c0 + ε z |
(6.10) |
|||
c z = c0 + εz2n, n = 1,2 3,… |
(6.11) |
||||
c z = c0 |
1 + εcosh |
z |
|
(6.12) |
|
L |
|||||
|
|
|
|||
A specific example from underwater acoustics is the SOFAR channel described by the Garrett–Munk profile:
c z = c0 1 + ε η− 1 + exp − η |
(6.13) |
The variable η = 2 z− z0
z− z0 z0 is defined in (6.13). This model has free parameters, namely, c0, ε, and z0. Typical values found in the literature are c0 = 1500 m/s, ε = 0.00737, and z0 = 1300 m. For the profile presented in (6.13), the positive z-axis is directed downward, a common definition used in underwater acoustics.
z0 is defined in (6.13). This model has free parameters, namely, c0, ε, and z0. Typical values found in the literature are c0 = 1500 m/s, ε = 0.00737, and z0 = 1300 m. For the profile presented in (6.13), the positive z-axis is directed downward, a common definition used in underwater acoustics.
For very large values of |z|, all of these profiles approach infinity and the modes vanish. At these extreme limits, sound is trapped in a waveguide-like structure due solely to the refractive nature of the sound speed. At the other extreme one often encounters the purely mathematical situation where c z
z = 0 at some value, z
= 0 at some value, z . In this case kz2
. In this case kz2  ∞ and the field must vanish as z
∞ and the field must vanish as z  z
z . This is a mathematical artifact of certain models and does not represent anything physical. An example with this behavior is the linear sound speed profile:
. This is a mathematical artifact of certain models and does not represent anything physical. An example with this behavior is the linear sound speed profile:
c z |
= c0 + εz |
(6.14) |
The sound speed equals zero at z = − c0 |
ε and physically relevant solutions do not exist |
|
for z < − c0
< − c0 ε.
ε.

It is possible to find examples of c(z) for which (6.9) becomes one of the well-known equations defining a special function. Consider a physical model where the sound speed profile can be written as a constant, c0, plus a function of position that is small relative to c0, at least in some interval z 
 z1,z2
z1,z2 :
:
c z = c0 + c z |
(6.15) |
Under this assumption (6.8) is approximated by a first-order Taylor expansion in c z
z c0:
c0:
|
kz2 = |
ω2 |
− kT2 |
≈ |
ω2 |
− 2 |
ω2 |
c z |
− kT2 kz20 |
− 2 |
ω2 |
c z |
(6.16) |
|||||
|
2 |
2 |
|
|
|
|||||||||||||
|
|
c |
|
|
c |
|
|
|
c |
0 |
|
|
|
|
c |
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
The term k2 |
, the wavenumber when c z |
= 0, is defined as |
|
|
|
|
|
|||||||||||
z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2 |
= |
|
ω2 |
− k2 |
|
|
|
|
(6.17) |
||||
|
|
|
|
|
|
c2 |
|
|
|
|
||||||||
|
|
|
|
|
|
z0 |
|
|
|
T |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Using (6.16) and (6.17) in (6.9) and a little rearranging gives the following form for the vertical mode equation:
− |
d2Z |
+ U z Z = EzZ |
(6.18) |
2 |
|||
|
dz |
|
|
The “potential energy” function, U(z), and energy, Ez, appearing in (6.18) are defined as
U z |
= 2 |
ω2 |
(6.19) |
||
|
|
c z |
|||
|
3 |
||||
|
|
|
c |
|
|
|
|
0 |
|
|
|
|
Ez = kz20 |
(6.20) |
|||
The special form of (6.18) is reminiscent of Schrödinger’s time-independent equation. It should be pointed out that the expansion in (6.16) is not necessary to massage (6.9) into this form. The identification of U and E with potential and energy level is for illustrative purposes, the quantities do not necessarily have units of energy.
A reasonable question is whether or not the modes predicted using (6.16) will describe solutions to the original form, (6.8). It is clear that in general the two sets will not match since at some point the condition c z
z
 c0 may be violated. This is not a concern if ideal boundary conditions are applied in the interval [z1, z2] where the approximation holds. To better under-
c0 may be violated. This is not a concern if ideal boundary conditions are applied in the interval [z1, z2] where the approximation holds. To better under-
stand the difference, (6.9) is cast in the same form as (6.9) by adding − k2 |
Z to both sides: |
||||||
|
|
|
|
|
|
z0 |
|
− |
d2Z |
+ k2 |
− k2 |
z |
Z = k2 |
Z |
(6.21) |
|
|||||||
|
dz2 |
z0 |
z |
|
z0 |
|
|
|
|
|
|
|
|
|
|
Comparing (6.21) with (6.18) with (6.16) serving as the potential, it is clear that the differences (and similarities) can be understood by comparing the following two effective potentials:
U2 z k02 = 2c z c0 |
(6.22) |

Depth (m)
|
|
|
Speed of sound (m/s) |
|
|
|
|
|
|
Effective potential |
|
|
|
|||||
1500 |
1510 |
1520 |
1530 |
1540 |
1550 |
1560 |
0 |
0.01 |
0.02 |
0.03 |
0.04 |
0.05 |
0.06 |
0.07 |
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–2000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–2500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–3000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–3500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–4000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–4500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–5000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Figure 6.1 The Garrettt–Munk sound speed profile (left) and its effective potentials (right)
U1 z k02 |
= |
1 + c z |
c0 2 − 1 |
(6.23) |
|
1 + c z |
2 |
|
|||
|
|
c0 |
|
||
Figure 6.1 illustrates the difference for the Garrett–Munk profile. The left pane is the sound speed profile plotted using (6.13). The right pane shows both effective potentials, (6.23) solid and (6.22) dashed. The potentials are scaled by k02 = ω2 c20 to avoid frequency dependence and provide a clear view of the functional form of these potentials. The relative difference between the two potential functions is less than 1% for z
c20 to avoid frequency dependence and provide a clear view of the functional form of these potentials. The relative difference between the two potential functions is less than 1% for z 
 585m, 2417m
585m, 2417m and less than 5% down to 4500 m. The figure clearly demonstrates the similarities between the two models for a range of values that correspond to expected ocean depths. Two more examples are shown to further illustrate some of these features. In all examples, solid lines represent the unperturbed potential, while dashed lines represent the first-order expansion given in (6.22). The first is for the linear profile in (6.14). The vertical axis is height in meters and the horizontal potential (no units). The pair of potentials is plotted for three values of ε, that is, 0.001, 0.005, and 0.01, which are plotted in Figure 6.2, shown from left to right. Attention should be given to the horizontal axis. It is clear that for increasing values of the sound speed deviation, the mismatch between the two becomes more severe. For ε = 0
and less than 5% down to 4500 m. The figure clearly demonstrates the similarities between the two models for a range of values that correspond to expected ocean depths. Two more examples are shown to further illustrate some of these features. In all examples, solid lines represent the unperturbed potential, while dashed lines represent the first-order expansion given in (6.22). The first is for the linear profile in (6.14). The vertical axis is height in meters and the horizontal potential (no units). The pair of potentials is plotted for three values of ε, that is, 0.001, 0.005, and 0.01, which are plotted in Figure 6.2, shown from left to right. Attention should be given to the horizontal axis. It is clear that for increasing values of the sound speed deviation, the mismatch between the two becomes more severe. For ε = 0 001, the relative difference is less than 1% for heights less than 6.5 m and less than 1.6% for those up to 10 m.
001, the relative difference is less than 1% for heights less than 6.5 m and less than 1.6% for those up to 10 m.
The last example is that of a quadratic refractive index. The sound speed profile for this case will be presented in the next section, (6.24). Plots of the two effective potentials are shown in Figure 6.3. In this case the shape parameter is fixed at ε = 0 001. The potentials are plotted for three distances away from the waveguide axis—100, 500, and 1000 m—from left to right. For the first case a relative difference is less than 0.1% over the entire range of position. It is clear that the two potentials fall far out of sync at larger distances, as to be expected since U2 is based on a first-order expansion. This example also illustrates how the approximate potential mimics the behavior of the sound speed profile. What these examples illustrate is that when ideal boundary conditions are included in the problem, (6.22) may be a good model for (6.23) and, as illustrated in the next section, may be easier to solve.
001. The potentials are plotted for three distances away from the waveguide axis—100, 500, and 1000 m—from left to right. For the first case a relative difference is less than 0.1% over the entire range of position. It is clear that the two potentials fall far out of sync at larger distances, as to be expected since U2 is based on a first-order expansion. This example also illustrates how the approximate potential mimics the behavior of the sound speed profile. What these examples illustrate is that when ideal boundary conditions are included in the problem, (6.22) may be a good model for (6.23) and, as illustrated in the next section, may be easier to solve.

9 |
|
|
9 |
|
|
9 |
|
|
8 |
|
|
8 |
|
|
8 |
|
|
7 |
|
|
7 |
|
|
7 |
|
|
6 |
|
|
6 |
|
|
6 |
|
|
5 |
|
|
5 |
|
|
5 |
|
|
4 |
|
|
4 |
|
|
4 |
|
|
3 |
|
|
3 |
|
|
3 |
|
|
2 |
|
|
2 |
|
|
2 |
|
|
1 |
|
|
1 |
|
|
1 |
|
|
0 |
0.01 |
0.02 |
0 |
0.05 |
0.1 |
0 |
0.1 |
0.2 |
0 |
0 |
0 |
Figure 6.2 Effect potentials for the linear sound speed profile at various strengths
100 |
|
|
|
500 |
|
1000 |
|
|
|
80 |
|
|
|
400 |
|
800 |
|
|
|
60 |
|
|
|
300 |
|
600 |
|
|
|
40 |
|
|
|
200 |
|
400 |
|
|
|
20 |
|
|
|
100 |
|
200 |
|
|
|
0 |
|
|
|
0 |
|
0 |
|
|
|
–20 |
|
|
|
–100 |
|
–200 |
|
|
|
–40 |
|
|
|
–200 |
|
–400 |
|
|
|
–60 |
|
|
|
–300 |
|
–600 |
|
|
|
–80 |
|
|
|
–400 |
|
–800 |
|
|
|
–100 |
0.005 |
0.01 |
0.015 |
–500 |
0.2 |
–1000 |
0 |
5 |
10 |
0 |
0 |
0.4 |
