The angular functions can be combined into one set of normalized functions on the unit sphere called spherical harmonics:

The radial equation is presented:

For l = 0 the solution is proportional to the spherical Green’s function:

The positive sign represents outgoing spherical waves from a point at r = 0, while the minus sign represents spherical waves coming from infinity and converging on r = 0. For other values of l, the dimensionless variable η = kr is defined, and (4.101) becomes the spherical Bessel’s equation:

The solutions of (4.103), spherical Bessel functions jn(η), are related to the Bessel functions of half integer order. Let Bn(η) represent any of the following functions: Bessel, Neumann, or Henkel. Then

π

jn η = ηBn + 1 2 η (4.104) 2

The three coordinate systems presented here are the most common. There are other separable coordinates. The reader is referred to Morse and Feshbach for additional details [8].

4.5 Boundary Conditions

The modes described in the last two sections are defined over all of space; their domain is unrestricted. Practical problems involve boundaries that restrict the domain of the solution and require specific behavior at the boundary. There are three types of boundary conditions to consider. Dirichlet boundary conditions restrict the value of the function at the boundary. Neumann boundary conditions place a constraint on the value of the normal derivative of the function evaluated at the boundary. Cauchy conditions impose a constraint on the value of the function and the normal derivatives at the boundary. An example of a Dirichlet boundary condition is a

pressure release surface, pxS = 0, where xS describes points on the boundary. The condition for reflection of pressure waves from an ideally hard surface is an example of Neumann boundary conditions, n∙ pxS = 0, where n is the normal to the surface. In general Cauchy conditions come in a variety of forms. Another type of boundary condition is the Robin condition:

One can also have mixed boundary conditions where the field and its normal derivate are restricted on disjoint regions of a boundary.

The application of ideal boundary conditions to cases with Cartesian symmetry is presented as an illustrative example. Consider two parallel infinite planes with normal vectors along the z direction, leaving waves free to propagate in the x–y plane. Boundary conditions are applied to a linear combination of the two independent solutions in the z coordinate.

For this example, the boundaries are at zBC = 0,Lz. There are three distinct choices of ideal boundary conditions: (1) two ideal pressure release surfaces, (2) two ideal hard boundaries, and

(3) one soft boundary and the other hard. To simplify equations the following variable is defined:

The first constraint implies a1 = − a0 and the functions satisfying this are sin(kzz). The second constraint, after applying the results of the first constraint, leads to the following condition:

This is satisfied only for kzLz = nπ, where n is an integer. The application of the first boundary condition fixes a node at z = 0, while the second places a restriction on the allowed wavenumber producing a discrete spectrum.

Case 4.2: Two Hard Boundaries

Ideal hard boundary conditions are imposed on both planes, n∙ ψz = zBC = 0, leading to

The first constraint implies a1 = a0 and the appropriate function satisfying this is cos (kzLz). The second constraint, evaluated at a1 = a0, leads to the same result for the discrete spectrum.

Case 4.3: One Pressure Release and One Hard Surface

Fixing the pressure release surface at Lz and the hard surface at 0, leads to the following for the boundary conditions:

Once again, the first constraint leads to a cosine function, while the second implies

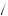The constraint is satisfied only for kzLz = 2n + 1π2.

The entire exercise of finding appropriate eigenfunctions for ideal boundary conditions in Cartesian coordinates boils down to fitting the trigonometric functions sine and cosine into the region between the boundaries such that nodes occur at a soft boundary and antinodes at a hard boundary. Results for all three cases are summarized in Table 4.2.

This completes the development of eigensolutions for these three cases of boundary conditions in one of three dimensions. The complete solution for any of the three cases may be expressed as follows:

Following the eigenvalue indexing discussed in the previous section, eigenfunctions for the cases described thus far are as follows:

The shorthand kT = kx, ky T for the 2-dim propagation vector in the x–y plane has been introduced.

The analysis presented earlier applies to pairs of surfaces in the other two Cartesian directions. There is no need to repeat the details. Following the same convention, boundaries are placed at xBC = 0,Lx and yBC = 0,Ly; all the results of Table 4.2 carry over with the appropriate variable replacing z. As an example, consider ideally hard boundaries applied to pairs of boundary plains in the y and z directions. Indexing the discrete wavenumbers by m and n, respectively, leads to the following for the discrete wavenumber:

In this case the wavenumber in the x direction is a continuous parameter, taking any real value, kx − ∞, ∞. The eigenfunctions for this case are denoted:

The functions Ym(y) and Zn(z) are taken from case 2 of Table 4.2. Continuing in this manner another pair of hard boundaries is added in the x direction. Introducing a third index and following all the same conventions leads to

These modes might be ideal for describing sound in an enclosed rectangular volume of space, such as a room, with ideal hard walls, floor, and ceiling. For simplicity, an eigenfunction and its set of eigenvalues are denoted by the triple index (l, m, n). The reader can develop other examples. Samples of the 1-dim modes for n = 1 are presented in Figure 4.1.

Table 4.2 List of eigenfunctions and eigenvalues for three ideal cases