
МЕХАНИКА ЖИДКОСТИ И ГАЗА МУ к выполнению РГЗ
.pdf
Результаты расчета Vc и Re для других скоростей движения воды сведем в таблицу 3.1.
Таблица 3.1– Результаты расчета расчета Vc и Re
|
υ,ì / ñ |
0,5 |
1,0 |
|
1.5 |
|
2.0 |
|
2.5 |
|
|
V 103,ì 3 / ñ |
0,981 |
1,962 |
|
2.943 |
|
3,924 |
|
4,905 |
|
|
c |
|
|
|
|
|
|
|
|
|
|
Re 10−3 |
41,8 |
83,5 |
|
125,3 |
|
167,1 |
|
209,0 |
|
|
Для выбора расчетных зависимостей коэффициента гидравлического |
|||||||||
трения определим значения соотношений 20 d/ |
и 500 d/Δ: |
|
|
|||||||
|
20 d/ Δ=20·50/0,3=3 333; |
и |
500 d/ Δ= 500·50/0,3=83 383. |
|||||||
|
В первом |
случае 20 d ∆ < Re < 500 d ∆, поэтому |
для расчета |
|||||||
коэффициента гидравлического трения применим уравнение Альтшуля:
|
∆ |
|
68 0,25 |
|
0,3 |
|
68 |
|
0,25 |
||
λ = 0,11 |
|
+ |
|
= 0,11 |
|
+ |
|
|
|
|
=0,0325 |
|
50 |
41,8 |
10 |
3 |
|||||||
d |
|
Re |
|
|
|
|
|
||||
Остальные значения критерия Рейнольдса (Re > 500 d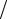 ∆) лежат в
∆) лежат в
автомодельной области , поэтому коэффициенты гидравлического трения будут одинаковы и их численные значения определяются по уравнению Шефринсона:
λ2 = λ3 = λ4 = λ5 = 0,11(∆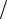 d )0,25 = 0,11(0,3
d )0,25 = 0,11(0,3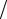 50)0,25 =0,0306
50)0,25 =0,0306
Определяем величину суммы коэффициентов местных сопротивлений, воспользовавшись таблицами Г.1 – Г.4.
4
∑ξ = 2ξâð +ξêò +3ξî +ξâû õ =2·4,6+3,05+3·1,265+1=17,045
i=1
гдеξâð =4,6 – коэффициент сопротивления вентиля регулирующего
dу=50 мм (таблица Г.4);
ξêò – коэффициент сопротивления крана трехходового. ξêò =3,05; ξî –коэффициент сопротивления отвода. Для стальных труб при угле
поворота потока α=90°ξî =1,265; ξâû õ –коэффициент сопротивления выхода потока из трубы. ξâû õ =1,0.
Определяем вид уравнения напорной характеристики сети, воспользовавшись общим уравнением (3.12) и уравнением секундного расхода (2.8):
|
p |
|
|
l |
4 |
υ2 |
|
p |
|
|
l |
4 |
8V |
2 |
|
|
||||
Hï î ò = hã + |
2 |
+ |
λ |
|
+ ∑ξi |
|
= hã + |
2 |
+ |
λ |
|
+ ∑ξi |
|
|
c |
|
= |
|||
ρg |
d |
2g |
ρg |
d |
π |
2 |
4 |
g |
||||||||||||
|
|
|
i=1 |
|
|
|
|
i=1 |
|
|
d |
|
|
|||||||
= 6 |
|
101,4 103 |
|
0,0325 |
20 |
+17,045 |
|
8 (0,981 10−3 )2 |
=16,882 м вод.ст. |
|||||
+ |
|
+ |
|
|
|
|
|
|
|
|
||||
986 9,81 |
0,05 |
3,14 |
2 |
0,05 |
4 |
9,81 |
||||||||
|
|
|
|
|
|
|
|
|
||||||
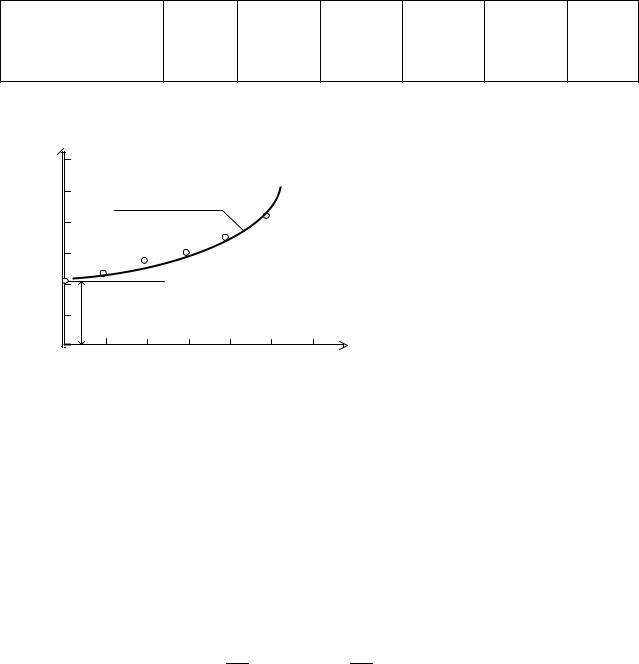
Для автомодельных режимов
40
|
|
|
|
p |
|
|
l |
4 |
|
υ2 |
|
p |
|
|
|
|
|
l |
|
|
4 |
8V 2 |
|
|
||||||||
Hï î ò |
= hã + |
2 |
+ |
λ2 |
|
+ ∑ξi |
2 |
|
= hã + |
|
2 |
+ |
λ2 |
|
|
+ |
∑ξi |
|
|
|
|
c |
|
= |
||||||||
ρg |
d |
|
ρg |
|
d |
π |
2 |
4 |
g |
|||||||||||||||||||||||
|
|
|
|
|
|
i=1 |
|
2g |
|
|
|
|
|
|
i=1 |
|
|
d |
|
|||||||||||||
= 6 |
|
101,4 103 |
|
0,0306 |
20 |
|
+17,045 |
|
|
8 (1,962 10−3 )2 |
|
|
|
|
|
|
|
|||||||||||||||
+ |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
||||||||
986 9,81 |
0,05 |
|
3,14 |
2 |
|
0,05 |
4 |
9,81 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
=16,5+387148Vc2
Для различных расходов по полученному уравнению находим значения потребных напоров. Результаты расчетов сводим в таблицу 3.2.
Таблица 3.2– Результаты расчета потребного напора
Секундный
расход Vc·103 , м3/с |
0,000 |
0,981 |
1,962 |
2,943 |
3,924 |
4,905 |
Потребный |
|
|
|
|
|
|
напор, Н, м вод.ст. |
16,5 |
16,88 |
17,99 |
19,85 |
22,46 |
25,82 |
По данным таблицы 3.2 строим напорную характеристику трубопровода
(рисунок 3.8).
Нпот
м вод.ст.
напор |
30 |
|
25 |
||
Потребный |
||
20 |
||
|
||
|
15 |
|
|
10 |
Hпот=Hn+kТVc2,0
Hn=hг+p2/ρg=16,5
Рисунок 3.8 – Напорная характеристика трубопровода по примеру 3.2
1 |
2 |
3 |
4 |
5 |
|
|
Секундный расход, Vc·103, м3/с |
||
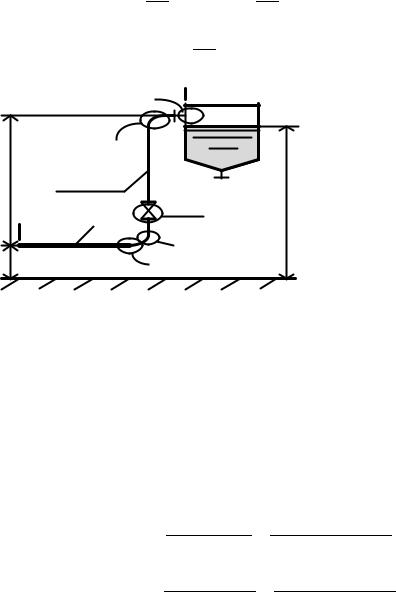
3.4.3.Гидравлический расчет трубопровода переменного сечения Пример 3.3 Для трубопровода из коррозионностойкой стали, схема
которого представлена на рисунке 3.9, рассчитать гидравлическое сопротивление. По трубам протекает 5 т/ч яблочного сока (динамическая вязкость μ=1,55·10–3 Па·с, плотность ρ = 1026 кг/м3). Длина первого участка составляет 20 м, второго – 40м. Геометрический перепад высот z = z1 – z2 равен 3,85м. Сок сливается в накопительную емкость, в которой поддерживается атмосферное давление.
Решение: Сечения 1 – 1 и 2 – 2 трубопровода объединим уравнением Бернулли относительно плоскости сравнения 0– 0:
Z1 + ρðg1 + α12gυ12 = Z2 + ρðg2 + α22gυ22 +∑hÏ
Для заданных условий потребный напор определяется как
41
|
|
Ð |
= (Z2 − Z1 )+ |
Ð |
|
α υ2 −α υ2 |
∑hï |
|
|
|||||
|
|
1 |
2 |
+ |
|
2 2 |
1 1 + |
= |
|
|||||
|
|
ρg |
|
|
|
|
ρg |
|
|
2g |
|
|
|
|
|
|
= ∆Z + |
Ð |
+ |
α υ2 −α υ2 |
|
+ h |
|
|
|
||||
|
|
2 |
2 2 |
1 1 + h |
|
|
|
|||||||
|
|
|
|
ρg |
|
|
2g |
|
|
ò ð |
ì ñ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ζ ВЫХ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
ζ К |
|
|
|
|
|
|
|
|
Рисунок |
3.9 |
– |
Гидравлическая |
|
|
∆z |
|
|
|
|
|
|
|
|
|||||
3.3 |
L2;d2 |
|
|
|
|
z2 |
|
|
схема трубопровода к примеру |
|||||
L1;d1 |
В-1 |
ζ |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
ζ К |
|
|
|
|
|
|
|
|
|
|
||
|
z1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
ζ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
BC |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Для каждого участка трубопровода (Ǿ 56х3,0 и Ǿ32х2,0) из уравнения массового секундного расхода определим среднюю скорость движения сока и его режим течения, учитывая, что условный проход для труб составляет соответственно 50 мм и 28 мм
υCP1 = |
|
|
4Q |
= |
|
4 5000 |
= 0,69ì |
/ñ |
||||
|
ρ π d 2 3600 |
|
1026 3,14 |
0,052 3600 |
|
|||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
υCP2 = |
|
4Q |
= |
|
4 |
5000 |
|
|
= 2,2ì |
/ñ |
||
|
3600ρ π d22 |
|
3600 1026 3,14 0,0282 |
|
||||||||
Re1 = υср1 µd1 ρ = 0,69 0,05 −10263 = 22386 1,55 10
Re2 = υср2 µd2 ρ = 2,2 0,028 −10263 = 40775 1,55 10
Установим область гидравлического трения с целью выбора расчетной зависимости для λ:
20d1 = 20 |
50 |
=16667; |
20 |
d2 |
|
= 20 |
28 |
= 9333; |
|||||||
∆ |
|
0,06 |
|
|
|
∆ |
|
|
0,06 |
|
|
||||
500d1 |
= 500 |
50 |
= 416675; |
500 |
d2 |
= 500 |
28 |
= 233325. |
|||||||
|
|
|
|
||||||||||||
∆ |
|
0,06 |
|
|
|
∆ |
|
|
0,06 |
|
|||||
где = 0,06 мм – высота неровностей (шероховатость) стенок трубы из коррозионностойкой стали (см. таблицу В.3)
Вышеприведенные расчеты показывают, что расчетные значения критериев Рейнольдса укладываются в область
20∆d < Re < 500∆d ,
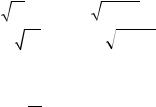
это позволяет рассчитать коэффициент трения по уравнению Альтшуля:
42
|
|
|
|
|
|
∆ |
+ |
68 |
|
0,25 |
|
|
|
|
|
|
|
|
|
|
|
|
λ = 0,11 |
Re |
|
. |
|
|
|
|
|
||
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
||
Подставляя численные значения, получим: |
|
|
|
|
|
|
|
|||||||||
|
|
0,06 |
|
68 |
|
0,25 |
|
|
|
|
0,06 |
|
68 |
|
0,25 |
|
λ1 |
= 0,11 |
|
+ |
|
|
= 0,028; |
λ1 = 0,11 |
|
+ |
|
|
= 0,027 |
||||
50 |
22836 |
28 |
40775 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Определим соответствующие имзначения коэффициентов Кориолиса:
α1 =1+ 2,65
 λ1 =1+ 2,65
λ1 =1+ 2,65
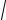 0,028 =1,44;
0,028 =1,44;
α2 =1+ 2,65
 λ2 =1+ 2,65
λ2 =1+ 2,65
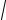 0,027 =1,44
0,027 =1,44
Рассчитаем потери напора на преодоление сил трения, воспользовавшись
уравнением Дарси–Вейсбаха hтр = λ l υ2 : d 2g
h |
= 0,028 |
20 |
|
0,692 |
|
= 0,27м; |
||||||
|
|
|
|
|
|
|||||||
тр1 |
|
|
0,05 |
|
2 9,81 |
|
|
|
||||
|
|
|
|
|
|
|
||||||
h |
|
= 0,027 |
|
40 |
|
|
2,22 |
|
= 9,52м |
|||
|
|
|
|
|
|
|
||||||
тр2 |
|
0,028 |
|
2 9,81 |
|
|||||||
|
|
|
|
|
||||||||
Гидравлические потери на преодоление местных сопротивлений
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
υ |
2 |
: |
|
|
|
|
|
|
||
определим по уравнениюДарси hмс = ∑ξi |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
2g |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
υ2 |
|
|
|
0,692 |
|
|
|
|
|
|
||
|
|
|
|
|
|
hмс1 = ξвс |
1 = 0,36 |
|
|
|
|
|
= 0,01м; |
|
|
||||||||||
|
|
|
|
|
|
2 |
|
9,81 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2g |
|
|
|
|
|
|
|
|
||||
h |
= (ξ |
|
+ξ |
|
+ 2ξ |
|
+ξ |
|
) |
υ2 |
= (6,1+0,36+ |
2 1,26+1,0) |
2,22 |
|
= 2,55 |
м. |
|||||||||
|
|
|
|
1 |
|
|
|||||||||||||||||||
|
|
|
|
2 9,81 |
|||||||||||||||||||||
MC2 |
|
 |
|
ÂÑ |
|
|
Ê |
|
|
ÂÛÕ |
|
2g |
|
|
|
|
|
|
|
|
|
|
|
||
Находим суммарный потребный напор по уравнению |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
Í |
|
= |
Ð |
|
= 3,85+ |
101,3 103 |
+ |
1,44 2,22 −1,44 |
0,692 |
+ |
|
||||||||||
|
|
|
|
ï î ò |
1 |
|
1026 9,81 |
|
|
|
|
2 9,81 |
|
|
|
||||||||||
|
|
|
|
ρg |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
+(0,27+9,52+0,01+2,55)= 26,6 |
|
|
|
|
|
|
|
||||||||||||||
Откуда гидравлическое сопротивление трубопровода составляет |
|
||||||||||||||||||||||||
|
|
|
|
|
|
∆Ð = ρgHï î ò |
=1026 9,81 26,6 = 267,5 кПа |
|
|
||||||||||||||||
3.4.4 Построение напорной характеристики трубопровода переменного сечения
Пример 3.4. В автоцистерну (рисунок 3.10) вместимостью V=2700 л заливается из резервуара спирт–сырец крепостью 90 % об. ( μ = 0,205·10-2 Па·с; ρ = 840 кг/м3) при располагаемом напоре Н = 12 м. Спирт заливается по трубе переменного сечения (l1=25 м; d1 = 50 мм; l2 = 35 м; d2 = 32 мм; 1 = 2 = 0,2 мм), имеющей три колена (ξк=0,8) и два прямоточных вентиля (ξв = 7,5). Определить время наполнения автоцистерны спиртом.
Решение: Время наполнения автоцистерны Т =V / Q зависит от расхода, а значит и от скорости течения спирта, которая, в свою очередь, зависит от
43
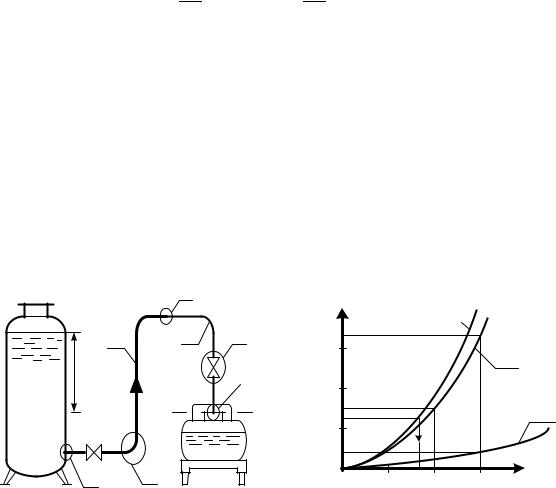
сопротивления трубопровода. Поскольку в общем случае коэффициент потерь на трение зависит от числа Рейнольдса, а значит и от скорости течения, то задачу об определении расхода можно решить либо способом последовательных приближений, либо графо–аналитическим способом.
С этой целью составляем уравнение Бернулли для сечений 1 – 1 и 2 – 2 относительно плоскости сравнения 0– 0. Вобщем случае уравнениеимеет вид:
Z1 + ρðg1 + α12gυ12 = Z2 + ρðg2 +α22gυ22 +∑hÏ
Для заданных условий (υ1 =0; р1 =р2 =ра; Z1= Н; Z2= 0) уравнение Бернулли примет вид:
Í = α22gυ22 +∑hï = α22gυ22 +∑hÏ 1 +∑hÏ 2 ,
где потери напора на участках трубопровода равны:
|
|
|
|
|
|
l1 |
|
|
|
|
|
8Q2 |
|
|
, |
|
||||
hÏ 1 = |
λ1 |
|
|
+ξâõ + 2ξê +ξâ |
+ |
|
|
|
|
|
|
|
|
|
|
|
||||
d |
|
g |
π |
2 |
d |
4 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
||||
hÏ 2 |
|
|
|
|
l2 |
|
|
|
|
|
|
|
8Q2 . |
|||||||
= |
|
λ2 |
|
|
|
+ξñ +ξê +ξâ +ξâû õ |
+ |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
g π |
2 |
|
4 |
|
||||||||||||
|
|
|
|
|
d2 |
|
|
|
|
|
|
d2 |
||||||||
|
ζс |
|
|
|
|
|
|
|
|
hп, м |
hп1+hп2 |
|
|
d1 |
d2 |
ζв |
|
|
|
|
32,99 |
|
|
|
|||
|
|
|
30 |
|
|
hп2 |
Н |
|
ζвых |
|
|
|
|
|
20 |
|
|
|
||
|
|
|
|
|
|
|
|
0 |
0 |
14,9 |
|
|
hп1 |
|
12 |
|
|
|||
|
|
|
10 |
|
|
|
|
|
|
3,89 |
|
|
|
ζвх |
ζк |
|
1 |
Q 2 |
3 |
Q,л/с |
а |
б |
Рисунок 3.10 |
– К примеру 3.4: |
а – гидравлическая схема трубопровода; б – графики потребного напора участков трубопровода
Коэффициенты местных сопротивлений примем равными: для входа в трубу ξвх = 0,5, для выхода из трубы ξвых = 1, а для внезапного сужения определим по уравнению Борда(таблица Г.2):
ξ |
|
|
d |
2 |
|
2 2 |
|
|
32 |
2 |
2 |
|
с |
= 0,5 1 |
− |
|
|
= 0,5 1 |
− |
50 |
|
|
= 0,3 |
||
|
|
d |
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Подставив значения величин, входящих в уравнения для определенияhп1 и
44
hп2, получим:
hï 1 |
|
|
25 |
+0,5+ |
2 0,8 |
+7,5 |
|
8Q2 |
|
|
= (66,2λ1 +1,27) 10 |
5 |
Q |
2 |
||||||||
= |
λ1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0,05 |
9,81 3,14 |
2 |
0,05 |
4 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
35 |
|
|
|
|
|
|
8Q2 |
|
|
|
= (864λ1 +8,58) 10 |
5 |
|
|
2 |
||||
hï 2 |
= |
λ2 |
|
|
|
+0,3 |
+7,5 |
+1+1 |
|
|
|
|
|
|
|
Q |
|
|||||
0,032 |
9,81 3,14 |
2 |
0,032 |
4 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Для построения кривых hп1 = f(Q) и hп2 = f(Q) по этим формулам проведем расчеты, результаты которых сведены в таблицу 3.2.
Таблица 3.2 – Результаты расчета требуемого напора трубопровода
Участок |
Расход |
Диаметр |
Скорость |
Критерий |
Коэффициент |
Напор |
трубопровода |
Q, л/с |
d, м |
ϑ,ì /ñ |
Рейнольдса |
трения |
hп, м |
|
|
|
|
Re×10−3 |
λ×102 |
|
|
1 |
50 |
0,51 |
10,45 |
3,52 |
3,6 |
1 |
2 |
50 |
1,02 |
20,90 |
3,21 |
13,8 |
|
3 |
50 |
1,53 |
31,35 |
3,08 |
29,78 |
|
1 |
32 |
1,24 |
16,262 |
3,52 |
3,89 |
2 |
2 |
32 |
2,49 |
32,525 |
3,32 |
14,9 |
|
3 |
32 |
3,73 |
48,766 |
3,25 |
32,99 |
При выборе формул для определения коэффициента гидравлического трения были использованы вспомогательные величины:
для первого участка:
20d1 |
= 20 |
50 |
= 5000; |
500 d1 |
= 500 |
50 |
|
=125000; |
||
0,2 |
0,2 |
|
||||||||
∆ |
|
|
|
∆ |
|
|
|
|||
для второго участка: |
|
|
|
|
|
|
|
|||
20d2 |
= 20 |
32 |
= 3200; |
500 |
d2 |
= 500 |
|
32 |
|
= 80000. |
∆ |
|
0,2 |
|
|
∆ |
|
0,2 |
|
||
Исходя из значений полученных величин установим вид формулы для расчета коэффициента гидравлического трения для первого и второго участка трубопровода:
|
∆ |
+ |
68 0,25 |
λ = 0,11 |
|
|
|
d |
|
Re |
|
По данным расчетов построены графики hп1 = f(Q) и hп2 = f(Q) и Σhп = f(Q) (рисунок 3.10б), с помощью которых по заданному значению Н = 12 м найден расход спирта Q = 1,62 л/с. Тогда время заполнения цистерны
Т = VQ = 27001,62 =1667с = 27,7мин
45
4 ПОДБОР НАСОСА И РАСЧЕТ ЕГО ТЕХНИЧЕСКИХ ПОКАЗАТЕЛЕЙ
4.1 Насосная установка и ее технические характеристики [26;с67 – 70];[1;с154 –158 ]
4.2.Подбор центробежного насоса [26;с71];[1;с167 –172 ]
4.3.Методы регулирования подачи центробежного насоса [26;с77 – 79];[1;с191 –194 ]
4.4.Примеры расчета и подбора центробежного насоса
4.4.1.Подбор насоса по каталогу
4.4.2.Определение рабочей точки насоса
4.3.3.Расчет эксплуатационных характеристик центробежного насоса
4.1Насосная установка и ее технические характеристики
Насосы относят к классу гидравлических машин, которые передают механическую энергию электродвигателя перекачиваемой жидкости. По принципу действия насосы делят на две группы. К первой группе отнесены насосы динамического типа, главным представителем которой является центробежный насос. Ко второй группе относятся насосы объемного типа, предназначенные в основном для перемещения высоковязких сред.
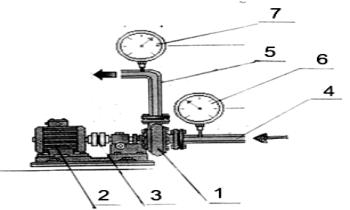
Насосы всегда работают в составе насосной установки ( рисунок 4.1). Помимо насоса 1 в состав установки входит электродвигатель 2 и соединительная муфта 3. Перекачиваемый продукт в установку поступает по всасывающему трубопроводу 4, а покидает ее по нагнетательному трубопроводу 5. Для контроля за работой насосной установки она снабжена контрольно измерительными приборами. Так на линии всасывания устанавливается моновакууметр 6, а на линии нагнетания манометр 7.
Рисунок 4.1– Схема насосной установки на базе центробежного насоса.
1–насос центробежный; 2– электродвигатель; 3– муфта; 4,5–линии всасывания и нагнетания; 6–моновакууметр; 7–манометр.
В центробежном насосе (рисунки Е.1–Е.4) основным его узлом (рабочим органом) является рабочее колесо с лопастями, установленное в рабочей камере (корпусе) насоса. Вследствие адгезии молекулы жидкости прилипают к поверхности деталей рабочего колеса. Поэтому жидкость, находящаяся в контакте с дисками и лопастями рабочего колеса, вращается вместе с ними.
46

Благодаря вязкости в совместное движение в рабочем колесе вовлекаются соседние слои и весь объем жидкости. Таким образом с помощью рабочего колеса жидкость увлекается в движение и механическая энергия электродвигателя преобразуется в кинетическую энергию потока.
Основными характеристиками насоса являются: производительность Vc , м3/с , (подача Q, л/мин); развиваемый напор Н, м вод. ст. (развиваемое давление р, Па); гидравлическая (полезная) мощность потока Nг, Вт; КПД насоса η. Кроме этих показателей к эксплуатационных характеристикам насоса относится глубина всасывания Нвс(м, м3⁄водс) .ст.
Производительность насоса характеризует количество жидкости, проходящей в единицу времени через нагнетательный патрубок насоса. Раньше этот показатель назывался подачей насоса, обозначалась
подача насоса через Q и имела размерность л/мин (1ë / ñ ≈10−3 ì 3 / ñ).
Давление, развиваемое насосом, ∆ð = ðí àã − ðâõ , |
(Па, МПа) – разность |
статических давлений жидкости в нагнетательном |
ðí àã и всасывающем |
патрубке насоса ðâõ . Ранее эта величина выражалась через напор Н,
развиваемый насосом (м вод. ст.). Напор характеризует удельную энергию, т.е. энергию, вносимую насосным агрегатом в единицу веса перекачиваемой жидкости. Связаны эти показатели друг с другом через основное уравнение гидростатики ∆ð = ρgH.
Полный напор, развиваемый насосом, определяется как разность энергий потока на выходе и входе в насос:
|
|
|
|
|
|
|
ð |
|
α |
υ |
2 |
ð |
|
α υ |
2 |
|
Í = Å1 − Å2 = ∑hní ã + z2 |
+ |
|
2 |
+ |
|
í ã |
í ã −(∑hnâñ − z1 + |
1 |
+ |
âñ |
âñ ) (4.1) |
|||||
ρg |
|
ρg |
||||||||||||||
|
|
|
|
|
|
|
|
|
2g |
|
|
2g |
|
|||
Из уравнения (4.1) следует, что: |
|
|
|
|
|
|
||||||||||
|
p |
2 |
− p |
|
α |
υ2 |
−α υ2 |
|
|
|
|
|||||
Í = ∆z + |
|
1 |
|
+ |
|
|
í ã |
í ã |
|
âñ âñ + ∑hn |
|
|
|
(4.2) |
||
|
ρg |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2g |
|
|
|
|
|
|||||
То есть напор, развиваемый насосом, тратится на подъем жидкости на требуемую высоту ∆z ; на преодоление разности давлений в емкости питания
и емкости нагнетания p2ρ−gp1 ; на преодоление разности скоростных напоров
в линиях всасывания и |
нагнетания |
α |
υ2 |
−α υ2 |
и на компенсацию |
|||
|
í ã í ã |
âñ âñ |
||||||
|
|
|
|
|
2g |
|
|
|
гидравлических |
потерь |
во |
всей |
трубопроводной |
системе: |
|||
∑hn = ∑hï í ã + ∑hï âñ
Гидравлическая (полезная) мощность потока–количество энергии,
вносимой насосом в единицу времени в единицу веса перекачиваемой жидкости.
Каждая единица веса жидкости, прошедшая через насос, приобретает энергию Н. За единицу времени через насос протекает жидкость весом ρgVc
47
Следовательно, энергия, приобретенная за единицу времени жидкостью, прошедшей через насос, считается полезной мощность насоса:
Nã = ρgVc H = ∆pH |
(4.3) |
Помимо гидравлической мощности потока различают мощность, потребляемую насосной установкой. Эта мощность является электрической и
обозначается как Ne (Вт). |
насосной |
установки |
|||
КПД η – |
коэффициент полезного действия |
||||
(электрической): |
η = Nã Nå =ηý ηì ηí |
|
|
|
(4.4) |
представляет собой отношение полезной мощности насоса |
|
к потребляемой |
|||
где ηý ;ηì ;ηí −КПД электродвигателя, муфты и насоса, соответственно.
Все перечисленные выше |
характеристики насоса могут быть |
||
представлены в виде графиков зависимости |
H (∆p)= f (VC ); |
NE (NÃ )= f (VC ); |
|
η = f (VC ); Зависимость H (∆p)= f (VC ) называется главной |
характеристикой |
||
насоса. На рисунке 4.2 в виде |
графиков |
представлены характеристики |
|
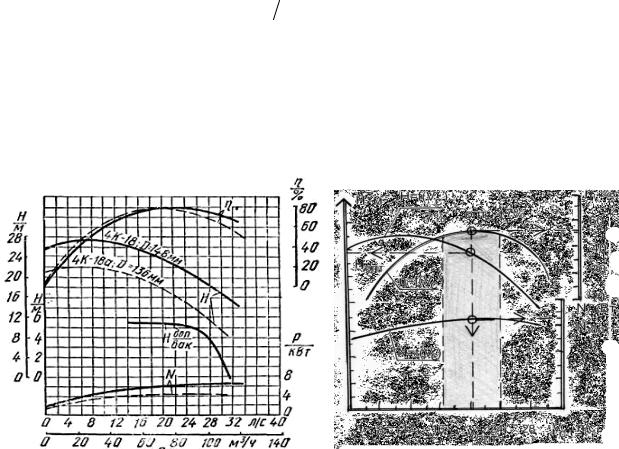
центробежного насоса К90/20(4К-18). |
|
|
|
а) б)
Рисунок 4.2 – Графические характеристики центробежного насоса К90/20(4К-18) (а) и его рабочая область (б)
Анализ главной характеристики центробежного насоса H=f(Vс) показывает, что с увеличением подачи насоса при постоянной частоте вращения рабочего колеса его напор H уменьшается. Лишь на коротком начальном участке кривой наблюдается незначительное повышение напора с возрастанием подачи. Этот участок характеризуется неустойчивой работой насоса, сопровождающейся толчками, ударами, а поэтому насос должен работать в области нисходящей ветви кривой. Вместе с тем в этой же области и лежат максимальные значения КПД насоса. Точка «опт», соответствующая
48
максимуму на кривой = ( с), является наиболее выгодной точкой и ей соответствует оптимальное значение подачи насоса Vопт, потребляемой
мощности Nопт и создаваемого напора Hопт.. При отклонении η от оптимальной точки его значение падает. Предельным снижением КПД от его
максимального значения является величина в (5÷7)%. Область подач насоса, ограниченная данным отклонением, называется рабочей областью насоса. На рисунке 4.2б рабочая область затенена.
Глубина всасывания (вакуумметрическая высота всасывания) зависит от разряжения (вакуума), которое создает центробежный насос на всасывающей стороне рабочего колеса. Теоретически (при полном вакууме) высота всасывания для воды при нормальном атмосферном давлении равном 1 ат = 101,32·103 Па составляет 10,33 м. Различают геометрическую и допустимую вакуумметрические высоты всасывания.
М Н Э
ЛВ
К
 Ф
Ф
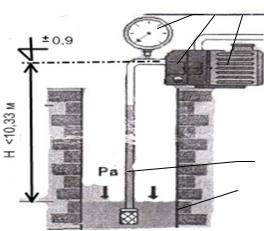
Рисунок 4.3 – К определению глубины всасывания насоса. К – колодец; ЛВ – линия
всасывания; М – моновакууметр; Н – насос; Э – электродвигатель; Ф – фильтр.
Подъем жидкости к рабочему колесу насоса по линии всасывания происходит вследствие избытка атмосферного давления на свободной поверхности жидкости в емкости питания над абсолютным давлением у входа в рабочее колесо, которое меньше атмосферного; эта величина и есть вакуум (вакуумметрическая высота всасывания), создаваемый насосом, т.е.
Í âàê = |
ðà − ð1 |
. |
(4.5) |
|
|||
|
ρ g |
|
|
У лучших современных конструкций насосов вакуумметрическая высота всасывания достигает 8,5 м вод. ст.
Геометрической высотой всасывания считается разность высот между нулевой отметкой или осью рабочего колеса насоса и свободной поверхностью жидкости в источнике или резервуаре, из которого она перекачивается. Она несколько меньше вакуумметрической высоты из-за потерь напора во всасывающей линии и требуемого запаса. Запас в высоте всасывания насоса называется кавитационным запасом и представляет собой разность между полным напором жидкости во входном патрубке насоса и давлением насыщенных паров:
49
