МЕХАНИКА ЖИДКОСТИ И ГАЗА МУ к выполнению РГЗ

2 РАСЧЕТ ПРОСТОГО ТРУБОПРОВОДА

2.1Классификация трубопроводов [26;с52];[1;с118 –122 ]

2.2Расчет характеристик потока [26;с25 –28];[1;с36;62 –65 ]

2.3Простой трубопровод [26;с53 –55];[1;с118 –122 ]

2.3.1Расчет диаметра трубопровода

2.3.2Определение наивыгоднейшей скорости

2.4Примеры расчета простого трубопровода

2.4.1Расчет характеристик потока

2.4.2Расчет диаметра трубопровода

2.1Классификация трубопроводов

Трубопроводами называют устройство, выполняемое из труб и других стандартных изделий (комплектующих), предназначенное для перемещения и транспортировки подвижных сред. В зависимости от назначения и рода перемещаемой среды различают: технологические трубопроводы, водопроводы, нефтепроводы, газопроводы, воздухопроводы и т. п.

Если движение жидкости происходит за счет разности ее геометрических высот в начале и в конце трубопровода, то такое течение называется самотечным, а трубопровод–безнапорным. Отличительным признаком безнапорного движения жидкости является наличие свободной поверхности, а давление в потоке равно атмосферному.

Движение жидкости в напорных трубопроводах происходит благодаря разности давлений (напоров) в начальном и конечном их сечениях. Эта разность давлений может быть создана при помощи насоса либо за счет уровня жидкости, либо под действием газа в резервуаре, из которого движется жидкость. При этом жидкость полностью заполняет все сечение трубопровода, а давление в трубопроводе выше атмосферного.

Все трубопроводы делятся на простые и сложные; длинные и короткие. К простым относят трубопроводы постоянного диаметра.

Короткими считаются трубопроводы сравнительно небольшой длины, в которых местные потери напора составляют не менее 5 – 10 % потерь напора на трение по длине. При их расчете исходят из принципа наложения потерь и принимая

Длинные–это трубопроводы значительной протяженности, в которых потери на преодоление местных сопротивлений составляют не более 5 – 10 % потерь напора по длине. При расчете их вовсе не учитывают, либо учитывают увеличение потерь напора на трение по длине на 5 – 10 %, т.е.

Все сложные трубопроводы выполняются, как правило, комбинированием из простых. Их основные виды приведены в классификации на рисунке 2.1.

20

Сложные

трубопроводы

Рисунок 2.1– Классификация трубопроводов

2.2 Расчет характеристик потока

Движение жидкости может быть установившимся и неустановившимся, равномерным и неравномерным, напорным и безнапорным, плавно изменяющимся и резко изменяющимся, ламинарным и турбулентным.

Установившимся называется такое движение жидкости, при котором скорость и давление в любой ее точке с течением времени не изменяются. При неустановившемся движении скорость и давление жидкости изменяются во времени.

Установившееся движение называется равномерным, если живые сечения потока, средние скорости и местные скорости в соответственных точках всех живых сечений одинаковы. В противном случае движение называется неравномерным.

Живым сечением называется поверхность внутри потока, нормальная к вектору средней скорости. Часть периметра живого сечения, соприкасающаяся с ограничивающими его твердыми стенками, называется смоченным периметром. Отношение площади живого сечения S к смоченному периметру

П называется гидравлическим радиусом потока rг

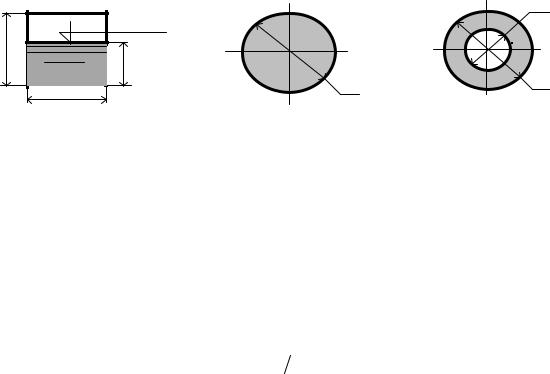
В случае же безнапорного движения жидкости смоченный периметр отличен от геометрического, т.к. линия, по которой жидкость соприкасается с воздухом, в длину смоченного периметра не входит. Так, в случае потока, перемещаемого в канале (см. рисунок 2.2а), смоченный периметр Ï = 2h + a , геометрический же параметр равен P = 2(b + a).

Для потока в кольцевом сечении гидравлический радиус определится как

21

Эквивалентный диаметр кольцевого потока будет соответственно равен

(D–d).

Рисунок 2.2 – Живые сечения потока а– безнапорного в канале; б–напорного в трубе, в– напорного в

кольцевом зазоре Помимо рассмотренных геометрических характеристик поток имеет и

кинематические. К их числу относят объемный (массовый) расход и скорости потока местную и среднюю.

Объемным расходом Vc ì 3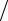ñ называется количество жидкости,

проходящее через живое сечение в единицу времени. Он может быть измерен объемным способом:

где V – объем мерного бака; м3 ; τ – время его наполнения; с.

При установившемся движении подвижной среды массовый расход среды МС [êãñ]через все живые сечения потока остается одинаковым:

гдеϑ1;ϑ2;...ϑï – средние скорости в выбранных живых сечениях;

S1, S2...Sn – площади этих живых сечений.

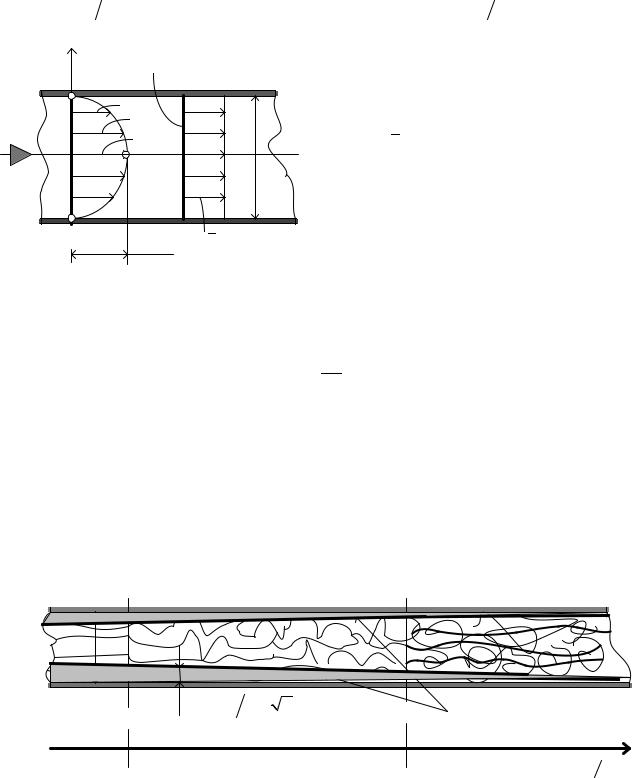
Будем рассматривать жидкостной поток, движущихся в цилиндрической

трубе. В потоке (рисунок 2.3) выделим плоское живое сечение, величиною S и вертикаль. За начало 1отсчета2 3 выберем нормаль N, которая принадлежит сечению. Векторами , , ,…обозначим скорости течения в различных

слоях потока . Эти скорости могут быть различными. Соединив концы векторов скоростей линией, получим фигуру NAM, которая представляет характер распределения скоростей по сечению потока. Эта фигура называется эпюрой скоростей.

Имея в виду неравномерность распределения скоростей в точках живого сечения, предложено в расчетах использовать среднюю скорость. Эту фактическую скорость обычно обозначают через . Средней скоростью υ

22

Рисунок 2.4–Схема режимов движения подвижных сред

23

Критерием для установления режима движения является безразмерное число Рейнольдса (критерий Рейнольдса):

где υ – средняя скорость движения потока, определяется из уравнения (2.9), м/c; dэ – эквивалентный диаметр потока, рассчитанный по уравнениям (2.4),(2.5),м; μ, ν и ρ – соответственно коэффициенты динамической (Па·с), кинематической (м2/c) вязкости и плотность (кг/м3) перемещаемой среды.

Переход от ламинарного режима движения к турбулентному характеризуется критическим значением Reкр, которое для круглых труб равно 2320. При значении Re < 2320 течение является устойчивым ламинарным. При Re>2320 чаще всего наблюдается турбулентный режим движения. Однако для области чисел Рейнольдса 2320 <Re <10000 режим еще неустойчиво турбулентный (эту область изменения Re называют переходной). И лишь при значениях Re > 10000 режим становится устойчиво турбулентным (развитым турбулентным). Значение Reкр зависит и от формы сечения канала. Так, для круглой трубы ReкрI=2300, а для кольцевого канала, поперечное сечение которого представлено на рисунке 2.2 в, ReкрI=1600. Объясняется это тем, что в кольцевом канале поверхность контакта между жидкостью и стенкой (смоченный параметр П в уравнении (2.3) больше, а следовательно, больше возникает локальных вихрей из–за шероховатости стенок и ламинарный режим быстрее сменяется турбулентным.

Re =ϑd ρ / µ

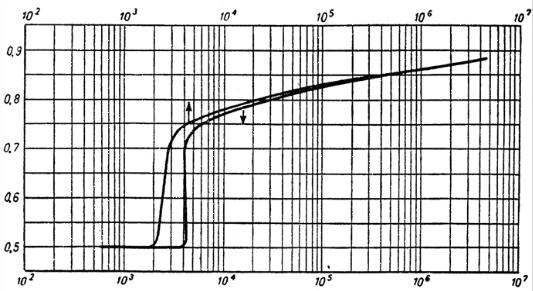
Рисунок 2.5–Зависимость отношения скоростей υ/ υmax от числа Рейнольдса для гладких круглых труб

В зависимости от режима течения меняется и соотношение средней скорости потока υ, рассчитанной по уравнению (2.8), к максимальной скорости

24

υmax по оси потока (см. рисунок 2.3), график этой зависимости приведен на рисунке 2.5

2.3 Простой трубопровод 2.3.1 Расчет диаметра трубопровода

Как известно, к простым трубопроводам относятся трубопроводы произвольной конфигурации с запорно–регулирующей арматурой постоянного диаметра. Такой трубопровод имеет среднюю скорость потока постоянную на всем своем протяжении. Т.е. скорость в начале трубопровода ϑ1 равна

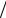скорости потока в конце трубопровода, а следовательно, и скоростные напоры в рассматриваемых сечениях будут одинаковы, а именно α1ϑ12 2g =α2ϑ22 2g .

При расчете такого трубопровода на первом этапе возникает необходимость в расчете его диаметра при известной пропускной способности Vc , м3/с и известных физических свойствах перемещаемой среды. Начинают расчет с назначения средней скорости движения среды с учетом условий движения и типа среды. Назначаемая скорость должна выбираться из рекомендуемых пределов, которые приводятся в таблицах приложений (например таблицы В.1 и В.2).

По известной пропускной способности и выбранной скорости движения потока из уравнения секундного расхода определяется площадь живого сечения потока. Учитывая форму живого сечения потока (круг, квадрат, прямоугольник и т.д.), находят определяющий геометрический размер потока. Так, для труб

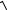
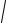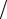круглого сечения don = 4Vc π ϑ2

Найденный определяющий геометрический размер потока необходимо согласовать с номенклатурой стандартных труб (таблицы В.4 – В.6) и выбрать ближайшую из труб, выпускаемых по ГОСТу. По принятому диаметру трубы dст рассчитывается средняя скорость движения среды. Полученные данные ϑcp

и dcm будут являться исходными данными для дальнейших расчетов.

Изложенная методика расчета иллюстрируется блок–схемой приведенной на рисунке 2.6.

Рисунок 2.6 – Блок – схема расчета диаметра трубы. 25

2.3.2 Понятие экономичной скорости

В простом трубопроводе ввиду постоянства его диаметра движение среды во всех его сечениях одинаково. Попробуем определить величину этой скорости, которая должна быть найвыгоднейшей с экономической точки зрения.

Положим, что имеем водопроводную сеть, выполненную из труб определенного диаметра. Представим теперь, что диаметр труб данной сети начинаем уменьшать. В результате этого получаем следующее: скорость

движения воды по сети возрастает (ϑ = 4Vc 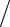(πd 2 ); потери напора в этих трубах

мощность насосов, перекачивающих воду (N = ρqHVc ). Т.е. можно утверждать,

что эксплуатационные затраты Э при этом возрастают.

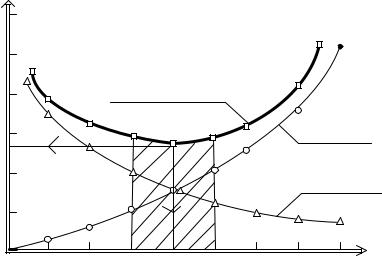
Также бесспорно выглядит и тот факт, что уменьшение диаметра труб магистрали снижает стоимость самой магистрали, т.е. величину капитальных затрат ЗК на ее сооружение. Приводя капитальные затраты (с учетом срока окупаемости) и эксплуатационные затраты к единице перемещаемой среды, строят графики зависимости Kпр=f(d) и Эпр=f(d) (см. рисунок 2.7). Тогда суммарные затраты Зпр выразятся кривой, полученной как сумма Зпр=Эпр+Кпр=f(d). Абсцисса dэ определяет область экономически выгодного диаметра, а следовательно, и диаметра, при котором приведенные затраты будут минимальными, т.е. Зпр→min.

о – график зависимости приведенных капитальных затрат Kпр=f(d);

∆ – график зависимости приведенных эксплуатационных затрат Эпр=f(d);

– результирующий график приведенных затрат Зпр=Кпр+Эпр=f(d)

Рисунок 2.7 – К определению экономически выгодного диаметра

26

= 3,148 (0,82 −134 0,0142 )=0,241 м2

2 Смоченный периметр потока:

Ï = 12(πD + nπd )= 3,142 (0,8+134 0,014)= 4,2

3 Эквивалентный диаметр:

dý = 4S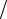Ï = 4·0,241/4,2 =0,229 м

Пример 2.2. Из30кожухотрубного конденсатора140 × 6 отводится аммиак= 16(R717) при температуре по трубе в количестве кг/с. Определить среднюю скорость движения аммиака в трубе.

Решение. По таблице Б.2 определяем плотность аммиака при температуре

+30°С, ρ = 595,5кг/м3

Площадь живого сечения трубы определим по ее внутреннему диаметру: d = dí − 2δ =140–2·6=128 мм S =πd 2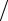4 =3,14·0,1282/4=0,0129 м2

Средняя скорость потока будет равна:

ϑcp = Mc 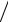(ρ S )=16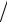(595,5 0,0129)=2,08 м/с

Пример 2.3 Необходимо установить режим движения 25 % водного раствора СаСl2 при температуре 30 °С во всасывающей линии насосной установки, если Мс=2,4 кг/с, а внутренний диаметр линии 80 мм.

Решение. По таблице Б.2 плотность 25 % раствора хлористого кальция ρ=1230,6 кг/м3, а его коэффициент динамической вязкости при заданной температуре μ=1,1·10–3 Па·с.

1 Находим объемный секундный расход рассола:

Vc = Mc 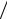ρ = 2,4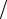1218,6 =1,97·10–3 м3/с. 2 Определяем среднюю скорость рассола в трубе:

3 Определяем коэффициент динамической вязкости рассола. Для этого определяем объемную долю соли в рассоле:

28

µñ = µ0 (1+ 4,5ϕð )=1,03 10−3 (1+ 4,5 0,173)=1,832 10−3 Ï à ñ

4 По найденной скорости рассчитываем значение критерия Рейнольдса:

Т.к рассчитанный критерий Re>Reкр2=104, то режим движения развитый турбулентный.

Пример 2.4 Определить массовый расход жидкого аммиака в трубе диаметром 150 мм, если скорость потока по оси трубопровода, измеренная трубкой Пито–Прандтля, составляет 3,2 м/с. Температура жидкого аммиака

0 °С.

Решение. По таблице Б.1 для жидкого аммиака при температуре 0 °С определяем его плотность ρ=638,6 кг/м3 и коэффициент кинематической

вязкости ν = 0,298 10−6 ì 2 / ñ.

1 Для измеренной скорости определяем максимальное значение критерия Рейнольдса:

Remax =ϑmaxd 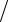ν = 3,2 0,15/0,298 10−6 =1,61·106

2 По графику (рисунок 2.5) для значения Remax=1,61·106 находим соотношение Re/Remax=0,87. Следовательно, значение критерия Рейнольдса определяемое по средней скорости, будет равно:

Re = 0,87 Remax = 0,87 1,61 106 =1,4 106

3 Откуда средняя скорость потока будет равна:

ϑ = Re ν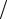d =1,4·106·0,298 10−6 /0,15=2,78 м/с

4 При такой средней скорости величина массового секундного расхода будет равна:

29