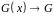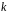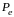РГР_Демчук

Завдання

Для розробки системи телекерування виконати наступне:

1 Для заданого інформаційного повідомлення 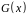й утворюючого полінома 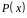знайти циклічний код :

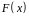а) як результат додавання добутку 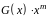із залишком ;

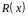б) як результат перемножування частки 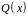на утворюючий поліном .

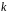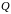2 Для заданої розрядності інформаційного повідомлення й утворюючого полінома визначити утворюючу матрицю . За допомогою утворюючої матриці знайти циклічний код для заданого інформаційного повідомлення .

3 Визначити коригувальні здатності заданого циклічного коду. Для заданої ймовірності 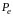спотворення одного розряду повідомлення оцінити ймовірність невиявлення помилок.

4 Для заданої розрядності інформаційного повідомлення й утворюючого полінома скласти таблицю залишків . Для розрахованого у п.п. 1, 2 циклічного коду та заданої комбінації помилок 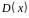записати прийняту спотворену комбінацію 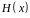. Користуючись таблицею, відновити код.

Визначимо номер варіанта за правилом :

,

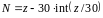де z – дві останніх цифри номера залікової книжки студента;

int(_*) – ціла частина числа.

z = 19 => N=19;

Таблиця 1 – Варіант завдань :

Варіант
15	10011	001000	6	10–3	0001000000

2 Загальна характеристика і принцип побудови циклічних кодів

Циклічні коди відносяться до лінійних систематичних розподільних кодів. Вони мають фіксовані кількість розрядів і місце розташування інформаційної й контрольної частин. При загальній довжині кодової комбінації 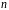розрядів і довжині інформаційної частини 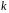розрядів код позначається як 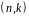код. У моєму варіанті завдання k = 6 , m=4, звідси n = m + k = 10 .

Циклічні коди будуються на основі операцій з інформаційними 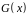і утворюючим 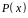поліномами (многочленами) у кінцевому полі двійкових чисел. Умовне подання двійкового коду у вигляді полінома полягає в заміні підстави 2 на фіктивну змінну х

Розрахунок:

А) результат додавання добутку 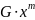і зал. R , m=4

Добуток:

.

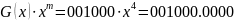Б) ділення:

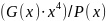
0010000000|10011

10011 001001 частка Q(x)

11000

10011

1011 залишок R(x)

Q(x)=001001,

R(x)=1011.

В) визначаємо комбінацію циклічного коду

,

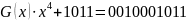0010000000

1011 R(x)

0010001011 F(x)

.

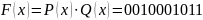001001 Q(x)

10011 P(x)

001001

001001

001001____

0010001011 F(x)

3 Метод утворюючої матриці

Для заданої розрядності інформаційного повідомлення й утворюючого полінома визначити утворюючу матрицю . За допомогою утворюючої матриці знайти циклічний код для заданого інформаційного повідомлення .

називається утворюючою матрицею коду.

Записуємо одиничну матрицю Е (К=6)

E= .

А) розрахуємо матрицю доповнень розміром (К*m)

1000000000|10011

10011 100110

R6:0011 0011

R5:0110 0110

1100

11000

10011

R3:1011 1011

10110

10011

R2:0101 0101

R1:1010 1010

Записуємо твірну матрицю:

U= = = .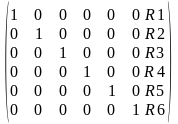

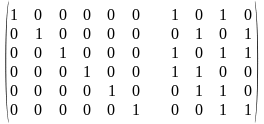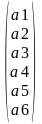Знаходимо кодову комбінацію для вектора G=001000

F = G*U = (001000)* =0010001011,

F=a3= 0010001011 = F(x).

Коригувальні здатності й завадостійкість циклічного коду

Коригувальні здатності циклічного коду визначаються вибором утворюючого полінома 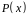і кількістю перевірочних розрядів m.

При цьому загальне число ненульових компонентів многочлена не повинне бути менше мінімальної кодової відстані 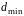=3. Таким чином цей циклічний код може знаходити одиночні й подвійні помилки, а виправляти тільки одиночні.

Розрахунок:

К = 6,

m = 4,

n = 10.

P(x) = ,

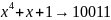Число сполучень із 10 елементів :

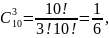
Визначаємо імовірність невиявлення помилок в циклічному коді :

, так як ,

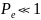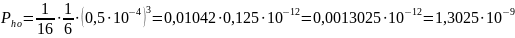
Таким чином ймовірність невиявлення помилок

Алгоритм виправлення одиночних помилок

При спотвореннях окремих розрядів у каналі зв'язку на прийомній стороні замість кодової комбінації циклічного коду 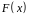виявляється кодова комбінація

,

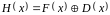де 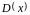– многочлен помилок, що містить одиниці на тих позиціях, де є спотворення прийнятої комбінації.

У цьому випадку в результаті розподілу спотвореної кодової комбінації 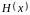на утворюючий поліном одержимо:

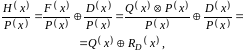
де 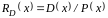– залишок (синдром), обумовлений наявністю спотворень.

Розрахунок:

D(x) = 0001000000, F(x) = 0010001011, H(x) = F(x) + D(x).

0010001011 F(x)

0001000000 D(x)

0011001011 H(x)

Будуємо таблицю відповідно до пункту 3 (Метод утворюючої матриці) ,а саме згідно значень MR :

D	R(x)
1000000000 0100000000 0010000000 0001000000(x) 0000100000 0000010000 0000001000 0000000100 0000000010 0000000001	1010 0101 1011 1100 R(x) 0110 0011 1000 0100 0010 0001

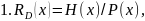
H(x) 0011001011|10011 P(x)

10010 010110

10110

10011

10111

10011

1100 RD(x)

,

,

,

.

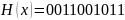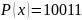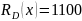2.

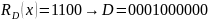
3. Виправлена кодова комбінація:

;

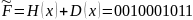0011001011 H(x)

0001000000 D(x)

0010001011 F(x)