
Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
(МТУСИ)

Кафедра: Сетевые информационные технологии и сервисы
Дисциплина: «Основы беспроводных коммуникаций»
Отчёт о практической работе №9
«Вычисление циклического контрольного кода»
Выполнил: Иванов И.И.
Группа: МБСТ0000
Вариант №**
Проверил: к.т.н., доцент Гадасин Д. В.
_________________________
Москва, 2023
Содержание
Y
Задание 3
Ход выполнения работы 4
Заключение 7
Задание
Вычислить CRC для строки кода задания 8 в соответствии со своим вариантом для порождающих полиномов.
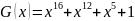
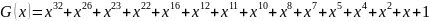
Провести проверку.
Взять первые две строки из диапазона строк своего варианта.
Номер варианта: 20
Таблица 1. Исходные данные для решения Задачи 9
№ варианта |
строка |
|
начальная |
конечная |
|
20 |
20 |
21 |
Текст для кодирования, который используется для решения Задачи 9:
ВСЕВОЗМОЖНЫХ СОБЫТИЙ ОКАЗЫВАЕТСЯ ЧЕТЫРЁХМЕРНЫМ ПРОСТРАНСТВОМ ГДЕ ТОЧКА СОБЫТИЕ ОПРЕДЕЛЯЕТСЯ ЧЕТЫРЬМЯ
Ход выполнения работы
Текст для кодирования
ВСЕВОЗМОЖНЫХ СОБЫТИЙ ОКАЗЫВАЕТСЯ ЧЕТЫРЁХМЕРНЫМ ПРОСТРАНСТВОМ ГДЕ ТОЧКА СОБЫТИЕ ОПРЕДЕЛЯЕТСЯ ЧЕТЫРЬМЯ
Таблица 2. Коды, полученные из 8 Задания для исходного текста
Символ |
Код |
Пробел |
000 |
Е |
001 |
О |
010 |
Т |
0110 |
С |
0111 |
Р |
1000 |
И |
1001 |
В |
1010 |
А |
1011 |
М |
1100 |
Н |
11010 |
Ы |
110110 |
Я |
110111 |
З |
11100 |
П |
111010 |
Ч |
1110110 |
Б |
1110111 |
Д |
111100 |
У |
1111010 |
Г |
11110110 |
К |
11110111 |
Щ |
1111100 |
Х |
11111010 |
Ё |
11111011 |
Л |
11111100 |
Ф |
11111101 |
Ь |
11111110 |
Ю |
111111110 |
Ж |
1111111110 |
Й |
11111111110 |
Ц |
11111111111 |
Кодирование строк
A(x)=10100111001101001011100110001011111111101101011011011111010000011101011101111101100110100111111111110000010111101111011111001101101010101100101100111110111000111011000101101101101000111110111111101011000011000110101101101100000111010100001001110110100010111101001110110101001011000001111011011110000100001100101110110111101111011000011101011101111101100110100100100001011101010000011111000011111110011011100101100111110111000111011000101101101101000111111101100110111
№1:
Таблица 3. Поиск контрольной суммы используя первый порождающий полином
А(x) |
Операция |
G(x) |
R(x) Остаток от деления |
10100111001101001011100110001011111111101101011011011111010000011101011101111101100110100111111111110000010111101111011111001101101010101100101100111110111000111011000101101101101000111110111111101011000011000110101101101100000111010100001001110110100010111101001110110101001011000001111011011110000100001100101110110111101111011000011101011101111101100110100100100001011101010000011111000011111110011011100101100111110111000111011000101101101101000111111101100110111 |
XOR |
10001000000100001 |
0010011111000000 |
Контрольная сумма равна = 0010011111000000
№2:
Таблица 4. Поиск контрольной суммы используя второй порождающий полином
А(x) |
Операция |
G(x) |
R(x) Остаток от деления |
10100111001101001011100110001011111111101101011011011111010000011101011101111101100110100111111111110000010111101111011111001101101010101100101100111110111000111011000101101101101000111110111111101011000011000110101101101100000111010100001001110110100010111101001110110101001011000001111011011110000100001100101110110111101111011000011101011101111101100110100100100001011101010000011111000011111110011011100101100111110111000111011000101101101101000111111101100110111 |
XOR |
100000100110000010001110110110111 |
00110000010111110101100110100010 |
Контрольная сумма равна = 00110000010111110101100110100010
Заключение
В ходе выполнения данной работы был получен остаток от деления закодированного текста на двоичную форму порождающих полиномов.
