Лаб 4 / Отчет 4
.docxМинистерство образования и науки Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования
Национальный исследовательский университет “МИЭТ”
Факультет Прикладных информационных технологий
Отчет по лабораторной работе №4
Вариант 7
Дисциплина: Численные методы
Выполнил:
Студент П-43
Губарев Сергей
Москва, 2022 год
Интерполяция функций
Цель работы: изучение методов решения задачи интерполяции; приобретение навыков программирования методов интерполяции; приобретение навыков использования стандартных средств системы Matlab для проведения интерполирования.
Ход работы
Задание 1 – 2
![]()
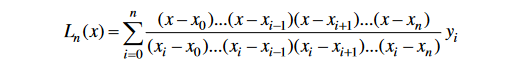
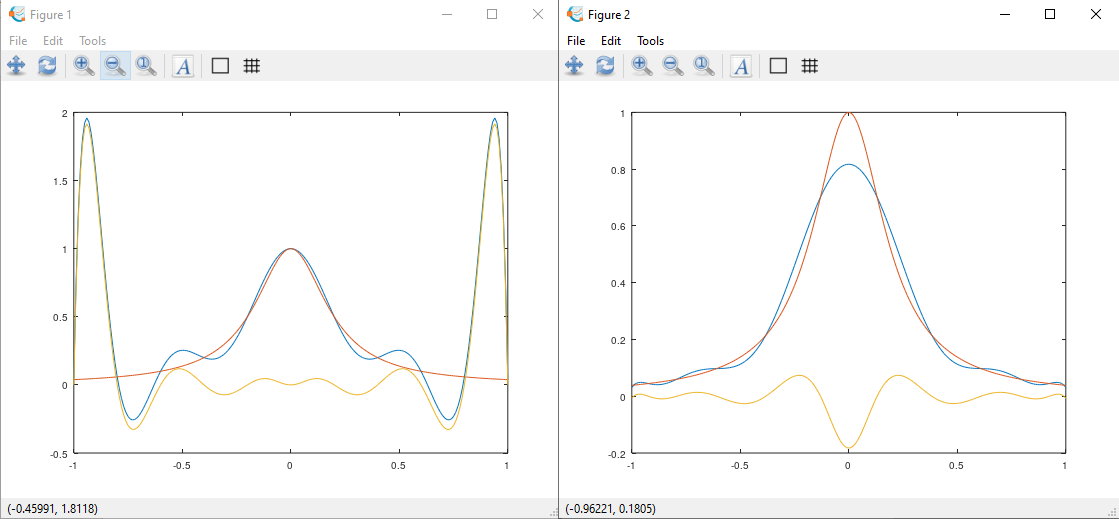
% задача 1. Провести интерполяцию функции Рунге на отрезке
% [–1, 1] по формуле Лагранжа для n = 11 при равномерном
% распределении узлов интерполяции.
% начало и конец отрезка
a=-1;
b=1;
% количество узлов
n=11;
% степень полинома
h=(b-a)/(n-1);
x=a:h:b;
% значение функции в точках х
f=1./(1+25*x.^2);
% для графика
X=a:0.01:b;
F=1./(1+25*X.^2);
nx=length(X);
% пустая матрица для решения многочлена лагранжа
L=zeros(1,nx);
% запускаем повторы для интерполяции
for i=1:n
% специальный базис
l=ones(1,nx);
for j=1:n
% проверяем условие спец базиса
if i~=j
% формируем специальный многочлен
l=l.*(X-x(j))./(x(i)-x(j));
end;
end;
% формируем многочлен
L=L+l.*f(i);
end;
% графики интерполяции
figure(1)
plot(X,L)
hold on;
% для функции рунге
plot(X,F)
hold on;
% погрешность
plot(X,L-F)
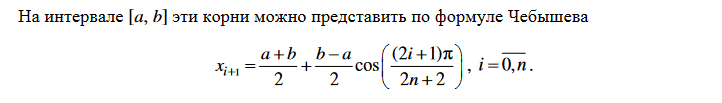
% задача 2. Провести интерполяцию функции Рунге на отрезке [–1, 1]
% по формуле Лагранжа для n = 11 для чебышевских узлов.
% матрица для интерполяции
h=(b-a)/(n-1);
x1=zeros(n,1);
% запускаем цикл на 11 повторов по всем узлам
for i1=1:n
% ищем по формуле интерполяции для чебышевких узлов
x1(i1,1)=(a+b)/2 + ((b-a)/2)*cos((2*i1+1)*pi/(2*n+2));
end
% значение функции
f1=1./(1+25*x1.^2);
% для графика
X1=a:0.01:b;
F1=1./(1+25*X1.^2);
nx1=length(X1);
% матрица для многочлена лагранжа
L1=zeros(1,nx1);
% запускаем повторы для интерполяции
for i1=1:n
% специальный базис
l1=ones(1,nx1);
for j1=1:n
% если выполняется условие специального базиса
if i1~=j1
% формируем оператор для посчета многочлена Лагранжа
l1=l1.*(X1-x1(j1))./(x1(i1)-x1(j1));
end;
end;
% формируем многочлен
L1=L1+l1.*f1(i1);
end;
% графики интерполяции
figure(2)
plot(X1,L1)
hold on;
% для функции рунге
plot(X1,F1)
hold on;
% погрешность
plot(X1,L1-F1)
Задание 3
% задача 3. Построить графики функции Рунге и ее интерполянт
% не менее чем в 100 узлах. Сравнить результаты.
a=-1;
b=1;
% количество узлов
n=100;
% степень полинома
h=(b-a)/(n-1);
x=a:h:b;
% значение функции в точках х
f=1./(1+25*x.^2);
% для графика
X=a:0.01:b;
F=1./(1+25*X.^2);
nx=length(X);
% пустая матрица для решения многочлена лагранжа
L=zeros(1,nx);
% повторяем прошлые действия (из заданий 1-2):
for i=1:n
l=ones(1,nx);
for j=1:n
if i~=j
l=l.*(X-x(j))./(x(i)-x(j));
end;
end;
L=L+l.*f(i);
end;
% графики интерполяции
figure(1)
plot(X,L)
hold on;
% для функции рунге
plot(X,F)
hold on;
% погрешность
plot(X,L-F)
Задания 4 – 6
% задача 4. Выбрать функцию согласно номеру компьютера и провести ее
% интерполяцию по формуле Лагранжа при равномерном распределении узлов
% на заданном интервале для n = 11 и n = 6.
clear
% начало и конец отрезка
a=0;
b=4;
% количество узлов
n=6;
% степень полинома
h=(b-a)/(n-1);
x=a:h:b;
% значение функции
f=x.^2 .* sin(2 .* x - 3);
% для графика
X=a:0.01:b;
F=X.^2 .* sin(2 .* X - 3);
nx=length(X);
% пустая матрица для решения многочлена лагранжа
L=zeros(1,nx);
% запускаем повторы для интерполяции
for i=1:n
% специальный базис
l=ones(1,nx);
for j=1:n
% проверяем условие спец базиса
if i~=j
% формируем специальный многочлен
l=l.*(X-x(j))/(x(i)-x(j));
end;
end;
% формируем многочлен
L=L+l.*f(i);
end;
% графики интерполяции
figure(1)
plot(X,L)
hold on;
% исходная функция
plot(X,F)
hold on;
% погрешность
plot(X,L-F)
% задача 5. Провести интерполяцию по тем же узлам, используя стандартные функции Matlab.
% интерполяция своей функции средствами Matlab
clear
% начало и конец отрезка
a=0;
b=4;
n1=11;
% степень полинома
h=(b-a)/(n1-1);
x1=a:h:b;
% значение функции
f1=x1.^2 .* sin(2 .* x1 - 3);
% для графика
X1=a:0.01:b;
F1=X1.^2 .* sin(2 .* X1 - 3);
% апроксимация методом наименьших квадратов через встроенную функцию
a=polyfit(x1,f1,n1);
% полином с коэффициентами из массива апроксимации а через встроенную функцию
A=polyval(a,X1);
% графики интерполяции
figure(2)
plot(X1,A)
hold on;
% исходная функция
plot(X1,F1)
hold on;
% погрешность
plot(X1,A-F1)
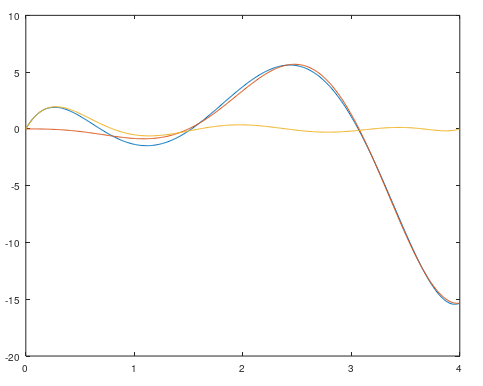
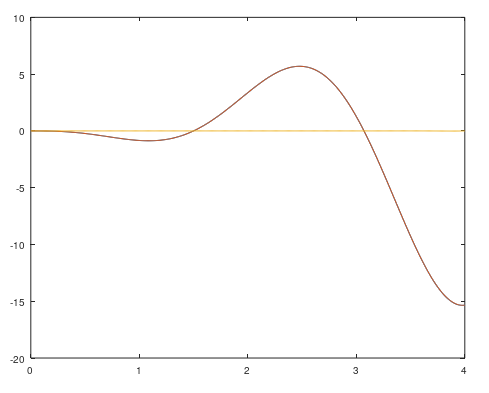
% задача 6. Построить графики исходной функции и интерполянт не менее
% чем в 100 узлах. Сравнить результаты.
clear
% начало и конец отрезка
a=0;
b=4;
n2=100;
h2=(b-a)/(n2-1);
x2=a:h2:b;
% значение функции
f2=x2.^2 .* sin(2 .* x2 - 3);
% для графика
X2=a:0.01:b;
F2=X2.^2 .* sin(2 .* X2 - 3);
nx2=length(X2);
% пустая матрица для решения многочлена лагранжа
L2=zeros(1,nx2);
% аналогично прошлым заданиям:
for i2=1:n2
l2=ones(1,nx2);
for j2=1:n2
if i2~=j2
l2=l2.*(X2-x2(j2))/(x2(i2)-x2(j2));
end;
end;
L2=L2+l2.*f2(i2);
end;
% графики интерполяции
figure(3)
plot(X2,L2)
hold on;
% исходная функция
plot(X2,F2)
hold on;
% погрешность
plot(X2,L2-F2)