
- •Семестр 1. Практическое занятие 1.1. Множество. Способы задания множеств. Отношения между множествами.
- •Практическое занятие 1.2. Операции над множествами.
- •Практическое занятие 1.3. Разбиение множества на классы. Декартово произведение множеств.
- •Практическое занятие 1.4. Число элементов в объединении, пересечении, разности и декартовом произведении множеств.
- •Практическое занятие 1.5. Понятия.
- •Практическое занятие 1.6. Высказывания и предикаты.
- •Практическое занятие 1.7. Конъюнкция и дизъюнкция высказываний и высказывательных форм. Отрицание высказываний.
- •Практическое занятие 1.8. Высказывания с кванторами.
- •Практическое занятие 1.9. Отношение следования и равносильности между предложениями. Структура теоремы. Виды теорем.
- •Практическое занятие 1.10. Умозаключения и их виды. Схемы дедуктивных умозаключений.
Практическое занятие 1.2. Операции над множествами.
Вопросы и задания для подготовки к занятию:
Дайте определения понятиям «объединение множеств», «пересечение множеств». Дайте этим операциям графическую иллюстрацию с помощью кругов Эйлера.
Сформулируйте свойства операций объединение и пересечение множеств. Проиллюстрируйте их с помощью кругов Эйлера.
Дайте определения понятиям «разность множеств», «дополнение множества». Дайте этим операциям графическую иллюстрацию с помощью кругов Эйлера.
Сформулируйте свойства разности множеств.
Известно, что
 .
Следует ли из этого, что:
.
Следует ли из этого, что:
Найдите пересечение, объединение, разность
[1; 5] и [3; 7];
А=

 ;
; ;
; и
и ;
;;

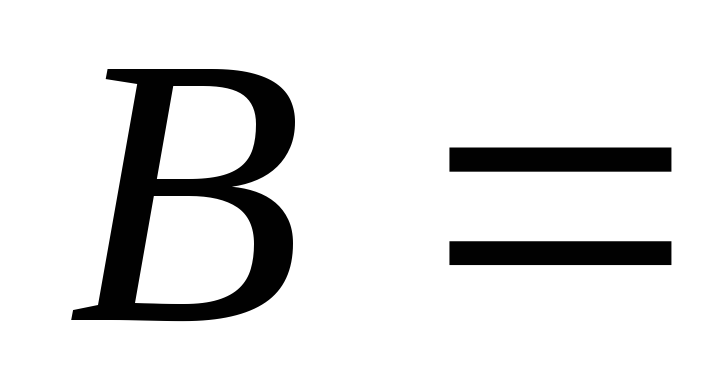 Ø..
Ø..
Известно, что
![]() .
Следует ли из этого, что:
.
Следует ли из этого, что:
Найдите разность числового отрезка [1; 5] и числового отрезка [3; 7].
Сформулируйте условия, при которых истинны следующие высказывания:
 ;
;
 .
.
Задания для самостоятельной работы
Перечислите элементы, принадлежащие пересечению множества букв в слове «математика» и множества букв в слове «грамматика». Из каких элементов состоит объединение данных множеств?
Р – множество натуральных делителей числа 18, Н – множество натуральны делителей числа 24. укажите характеристическое свойство элементов пересечения множеств Р и Н и перечислите его элементы.
Найдите пересечение и объединение множеств К и М, если К – множество двузначных чисел, М – множество нечетных чисел. Верно ли, что: а) 21
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г) .
.Н
 айти
объединение и пересечение множеств А
и В, если
айти
объединение и пересечение множеств А
и В, если и
и .
.Три множества Р, Н, М изображены тремя прямоугольниками (рис. 1). Отметьте штриховкой области, изображающие множество Х: а) М
 Н;
б) Р
Н;
б) Р Н;
в) (Р
Н;
в) (Р Н)
Н)
 (Н
(Н М).
М).
Рис. 1.
В – множество правильных многоугольников, Т – множество прямоугольников. Из каких фигур состоит объединение и пересечение множеств В и Т. Нарисуйте по две фигуры из каждого множества.
Даны множества: А ={а, b, с, d, е}, В ={с, d, f, k}, С = {b, с, d, f, m}. Перечислите элементы множеств К=(АВ)С и Р =А В С. Содержится ли элемент m в множестве К, а элемент f в множестве Р?
А – множество чисел, кратных 2, В – множество чисел, кратных 3, С – множество чисел, кратных 5. Укажите характеристическое свойство элементов множества (А
 В)
В) С
и (А
С
и (А В)
В) С.
С.Найдите объединение и пересечение множеств и дайте графическую иллюстрацию при помощи диаграмм Эйлера - Венна, если:
а) А = {5, 6, 7, 8, 9, 10}, В = {8, 9, 10, 11};
б) А= {х х = 5п, п N}, В= {х ÷ х = 2п, п ÎN};
г) А={х ÷ х = 2п, п ÎN}, В= {х ÷ х = 2п, п ÎN}.
Изобразите на числовой прямой и запишите при помощи неравенства объединение и пересечение множеств Р и Q:
а) Р =
![]() , Q=
, Q=![]() ;
;
б) Р =
![]() ,Q =
,Q =
![]() ;
;
в) Р =![]() ,Q
=
,Q
=
![]()
Множество А состоит из натуральных чисел от 2 до 10, множество В – из натуральных чисел от 5 до20. Перечислите элементы множеств А \ В и В \ А.
Р – множество двузначных чисел, М – множество четных натуральных чисел. изобразите данные множества при помощи кругов Эйлера, отметьте штриховкой разность множеств Р и М и укажите характеристическое свойство элементов, принадлежащей этой разности. Верно ли, что Р \ М содержит числа 21; 17?
Дано множество
 .
Запишите два подмножества множества
Х и дополнение этих подмножеств до
множества Х.
.
Запишите два подмножества множества
Х и дополнение этих подмножеств до
множества Х.Сформулируйте характеристическое свойство элементов дополнения множества Р до множества треугольников, если: а) Р – множество остроугольных треугольников; б) Р – множество равносторонних треугольников.
Найдите дополнение множества У до множества Х, если:
Х – множество точек прямой АВ;
множество точек отрезка АВ;
Х – множество точек квадрата, У – множество точек круга, вписанного в этот квадрат.
Найдите дополнение:
множества четных натуральных чисел до множества N;
множества отрицательных чисел до множества Z;
множества целых чисел до множества Q.
Отметьте на координатной прямой множество А и укажите характеристическое свойство элементов его дополнения до множества R, если: а)
 ;
б)
;
б)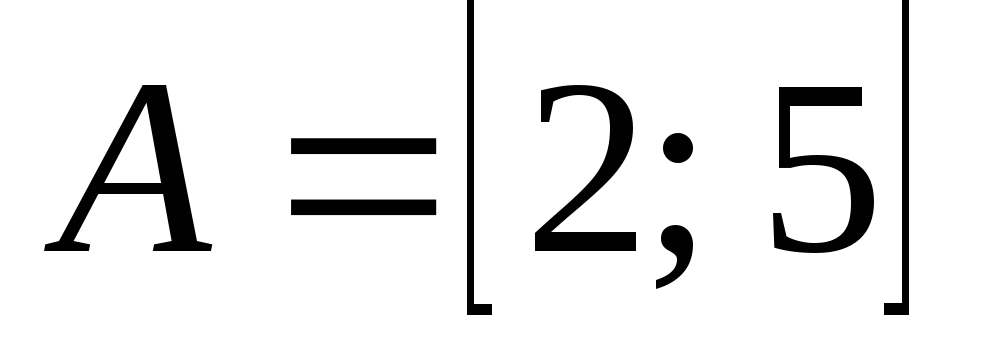 ;
в)
;
в) .
.Множества А, В и С таковы, что
 Ø.
Изобразите их при помощи кругов Эйлера
и отметьте штриховкой области,
представляющие множества (А \ В)
Ø.
Изобразите их при помощи кругов Эйлера
и отметьте штриховкой области,
представляющие множества (А \ В) С,
А \ В
С,
А \ В С,
А
С,
А (В
\ С), А
(В
\ С), А В
\ С. Для каждого случая сделайте отдельный
чертеж.
В
\ С. Для каждого случая сделайте отдельный
чертеж.А – множество прямоугольников, В – множество правильных многоугольников, С – множество треугольников. постройте круги Эйлера для данных множеств и отметьте штриховкой области, изображающие множества: а) А
 В
В С; б)
С; б)
 В
В С;
в) (А
С;
в) (А В)'
В)' С.
С.Постройте три круга, изображающие три попарно пересекающихся множества А, В и С, и выделите штриховкой области, представляющие множества:
а) АВ\С, б) А\СВ\С; в) А\(ВС).
