Практическое занятие 2.3.Комбинаторные задачи и их решение.

Вопросы и задания для подготовки к занятию:

1. Сколькими способами можно переставить буквы в слове «математика»?

2. Сколько разных комбинаций можно дать на 2, 3, 4, 5, 8 вопросов, если на каждый вопрос отвечать «да» или «нет»?

Задания для самостоятельной работы

1. Сколькими способами можно обить 6 различных стульев, если имеется 12 сортов обивочного материала?

2. В доме отдыха каждый день на десерт дали либо яблоко, либо апельсин, либо мандарин. В течение дней было выдано 9 яблок, 7 мандаринов и 8 апельсинов. Сколько различных вариантов могло быть?

3. Четверо студентов сдают экзамен. Сколькими способами им могут быть поставлены отметки, если известно, что ни один из студентов не получит неудовлетворительной оценки?

4. Сколько различных слов можно получить, переставляя буквы в слове «кукушка»?

5. Во взводе 5 сержантов и 50 солдат. Сколькими способами можно составить наряд из одного сержанта и трех солдат?

6. Сколькими способами можно образовать из группы в 12 мужчин и 8 женщин комиссию, так чтобы она состояла из 3 мужчин и 4 женщин?

7. Сколькими способами можно расставить 12 белых и 12 черных шашек на 32 черных полях?

8. Сколькими способами можно разделить 15 яблок и 20 апельсинов между тремя мальчиками?

9. Сколько имеется различных шестизначных чисел, у которых три цифры четные, а 3 - нечетные?

10. В кружке художественного слова занимаются 15 человек, в фортепианном – 10, в вокальном – 13 и в фотокружке – 20 человек. Сколькими способами можно составить бригаду из 4 чтецов, 3 пианистов, 5 певцов и одного фотографа?

Практическое занятие 2.4.Алгоритмы

Вопросы и задания для подготовки к занятию:

1. Толкование понятия «алгоритм».

2. Происхождение термина «алгоритм».

3. Свойства алгоритмов.

4. Способы записи алгоритмов.

5. Виды алгоритмов.

6. Установите, для решения каких задач используются следующие алгоритмы:

Алгоритм А.

1. Пишу единицы под единицами, десятки под десятками, сотни под сотнями.

1. Складываю единицы: 4 + 2 = 6.

2. Складываю десятки: 6 + 4 = 10, десять десятков равны одной сот­не. Пишу под десятками 0, а одну сотню запомню и прибавлю к сотням.

3. Складываю сотни: 2 + 5 = 7, да еще 1, получится 8. Пишу 8 под сотнями.

4. Читаю ответ: 806.

Алгоритм Б.

1. Отметь на листе бумаги точку О.

2. Установи раствор циркуля равным длине отрезка АВ.

3. Поставь ножку циркуля в точку О.

4. Проведи окружность.

7. Объясните, почему следующая программа действий является алгоритмическим предписанием:

Собери портфель

1. Открой портфель.

2. Положи в портфель тетради.

3. Положи в портфель учебники.

4. Положив портфель карандаш

5. Положив портфель ручку.

6. Закрой портфель.

8. Составьте алгоритм построения отрезка длиной 5 см. Какие изменения произойдут в нем с изменением длины отрезка?

Задания для самостоятельной работы

1. Является ли следующая программа действий алгоритмом или алгоритмическим предписанием:

А. Измерение длины отрезка АВ.

1. Совместить линейку с отрезком АВ, совместив 0 с А.

2. Отметить число, соответствующее точке В.

3. Записать полученное значение.

Б. Построение биссектрисы угла.

1. Провести циркулем дугу окружности, пересекающую стороны данного угла, и с центром в вершине угла.

2. Обозначить точки пересечения дуги окружности со сторонами угла буквами А и В.

3. Провести окружность с центром в точке А и тем же радиусом.

4. Провести окружность с центром, в точке В и тем же радиусом.

5. Обозначить одну из точек пересечения окружностей буквой С.

6. Провести луч из вершины угла через точку С.

2. Составьте алгоритм вычисления по формуле:

   1. у = (5х-3) · (2х+7);

   2. у = 2. (х +8) - 1.

3. По приведенному алгоритму восстановите формулу для вычисления значения у:

1. Умножить х на 4, обозначить ре­зультат R1.

2. Сложить R1 с числом 7, обозна­чить результат R2.

3. Разделить R2 на х, считать резуль­тат значением у.

2. Составьте алгоритм вычислении в миллиметрах длины ломаной, состо­ящей из:

   1. двух звеньев;

   2. пяти звеньев

3. Алгоритм решения неравенства х+2440 методом перебора задан при помощи блок схемы. Восстановите пропущенные шаги.

2. Составьте и запишите алгоритм построения на клетчатой бумаге квад­рата со стороной 5 см. Какие изменения надо внести в него, чтобы построить квадрат: а) со стороной 5 см на нелинованной бумаге; б) со стороной любой длины?

3. Используя прием пошаговой детализации, составьте алгоритм выполнения задания: «Определите логическую структуру и значение истинности высказывания, запишите его, используя символы». Про­верьте правильность составленного алгоритма для следующих выска­зываний:

   1. 28 кратно 4 и меньше 31;

   2. 28 кратно 4 или 9;

   3. неверно, что 28 кратно 9.

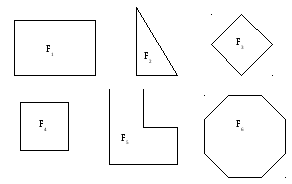
4. Используя определение квадрата, составьте и запишите алго­ритм, позволяющий среди различных геометрических фигур распо­знавать квадраты. Применяя его, выполните задание: «среди следую­щих фигур выделите квадраты».

2. Используя задание: «лежат ли три точки на одной прямой, если известны расстояния между ними: а) 3, 5, 8; б) 1, 4, 2; в) 6, 4, 5; г) 7, 11, 4; д) 3, 8, 12; е) 3, 6, 3?», разделите все случаи на группы в зависимости от результата; обобщите полученные выводы и постройте алгоритм принадлежности трех точек одной прямой. Каким приемом построения алгоритма вы воспользуетесь?

Примечание: расстояния между точками измерены с помощью одной и той же единицы длины.