
- •2011 Г.
- •20____ Г. Литература
- •§ 1. Основы молекулярно-кинетической теории газов.
- •§ 2. Явления переноса в газах.
- •§ 3. Первое начало термодинамики.
- •§ 4. Второе начало термодинамики.
- •§ 5. Реальные газы и жидкости
- •§ 6. Тепловые свойства твердых тел. Фазовые переходы.
- •Пример оформление задачи
- •Примерный перечень вопросов, выносимых на экзамен семестра
§ 4. Второе начало термодинамики.
Коэффициент полезного действия (КПД) тепловой машины:
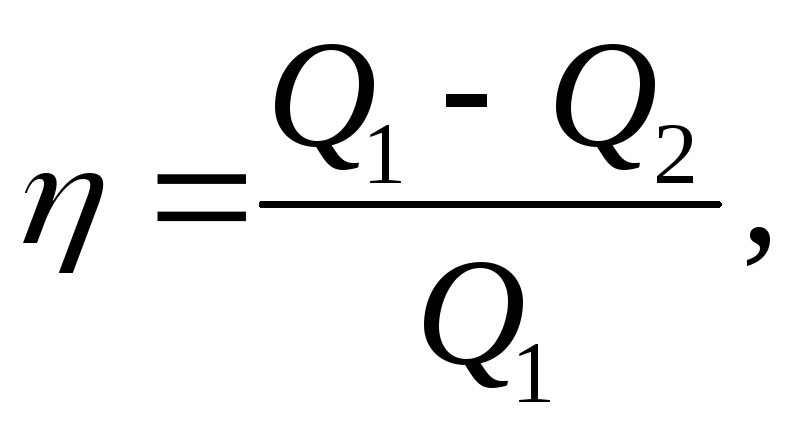 где
где -
количество теплоты, полученное рабочим
телом от нагревателя,
-
количество теплоты, полученное рабочим
телом от нагревателя, -
количество теплоты, переданное рабочим
телом холодильнику.
-
количество теплоты, переданное рабочим
телом холодильнику.КПД идеального цикла Карно:
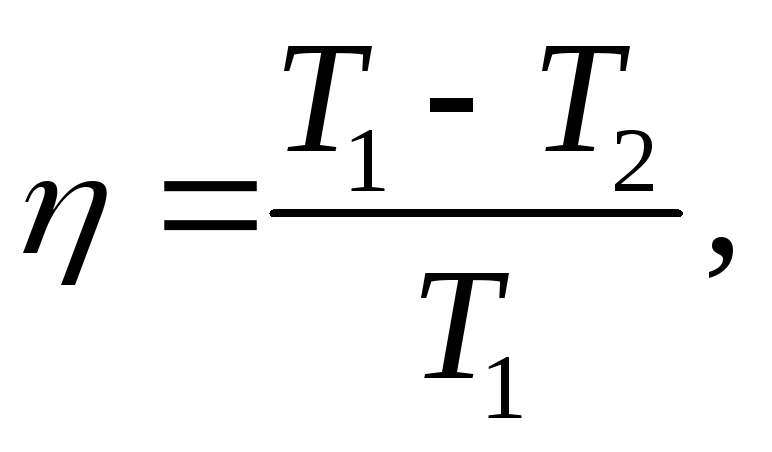 где
где - температура нагревателя,
- температура нагревателя,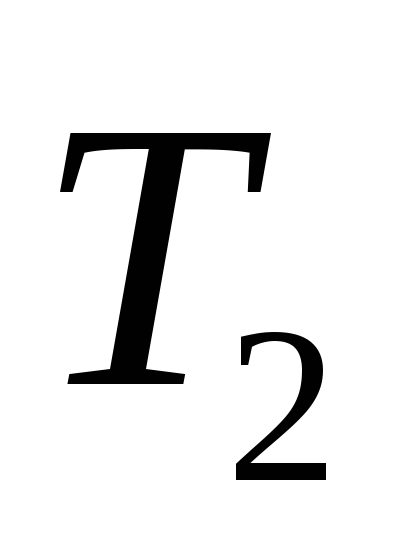 - температура холодильника.
- температура холодильника.Холодильный коэффициент холодильной машины:
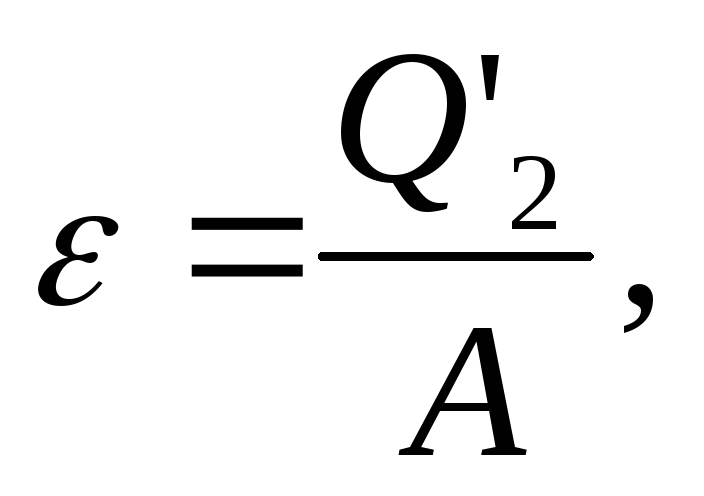 где
где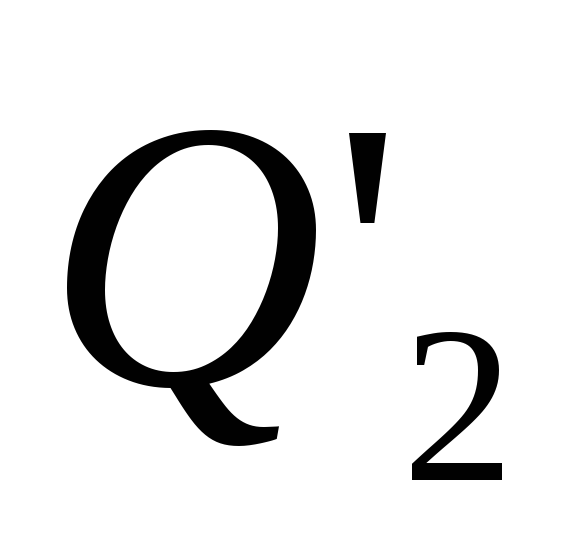 -
количество теплоты, отнятое от
охлажденного тела за цикл,
-
количество теплоты, отнятое от
охлажденного тела за цикл, -
работа, совершенная над газом за цикл.
-
работа, совершенная над газом за цикл.Приращение энтропии при переходе системы из состояния 1 в состояние 2:
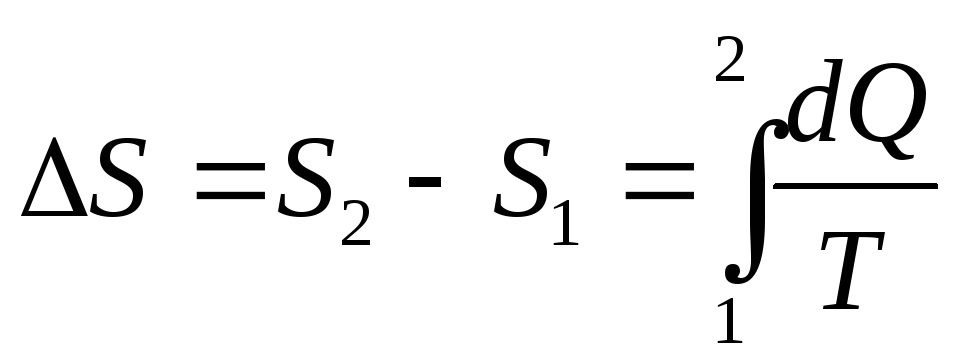
§ 5. Реальные газы и жидкости
Уравнение Ван-дер-Ваальса для произвольной массы
 газа: ,где
газа: ,где и
и - постоянные Ван-дер-Ваальса. Связь
критических параметров – молярного
объема, давления и температуры газа с
постоянными
- постоянные Ван-дер-Ваальса. Связь
критических параметров – молярного
объема, давления и температуры газа с
постоянными и
и
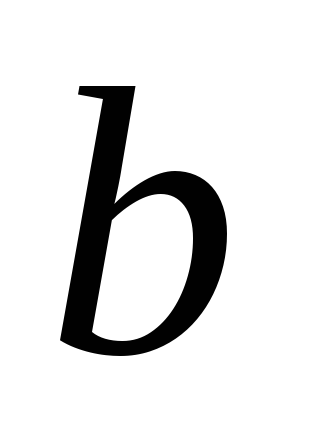 Ван-дер-Ваальса:
Ван-дер-Ваальса: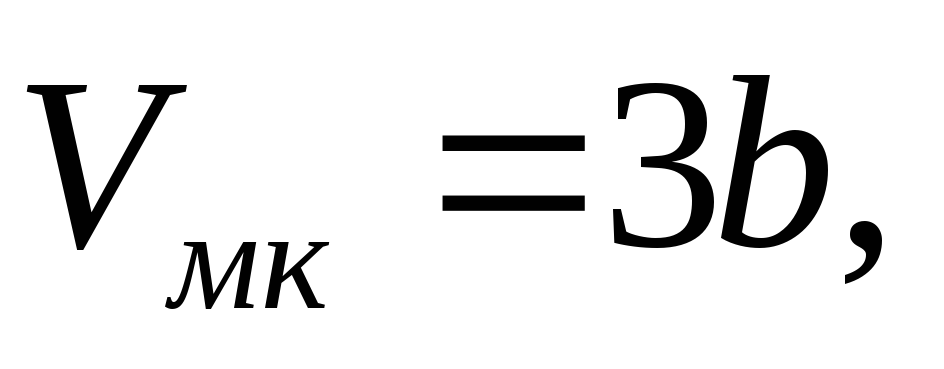
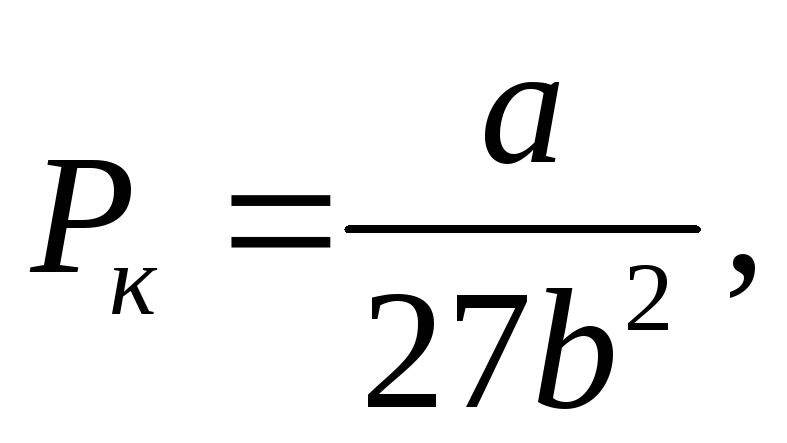
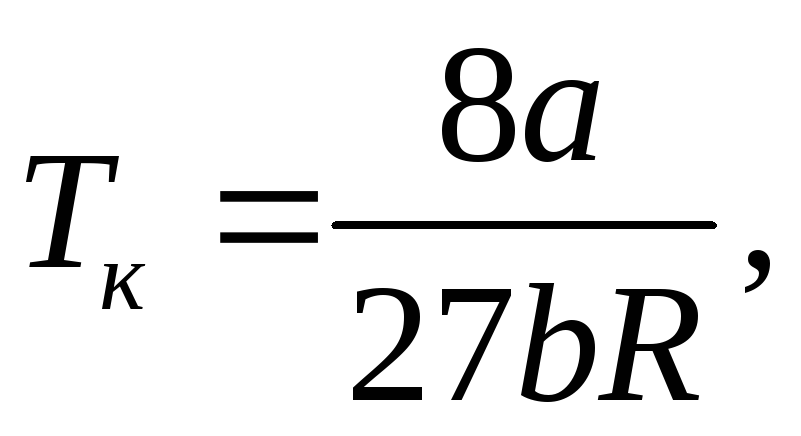
Уравнение Ван-дер-Ваальса в приведенных величинах для одного моля:
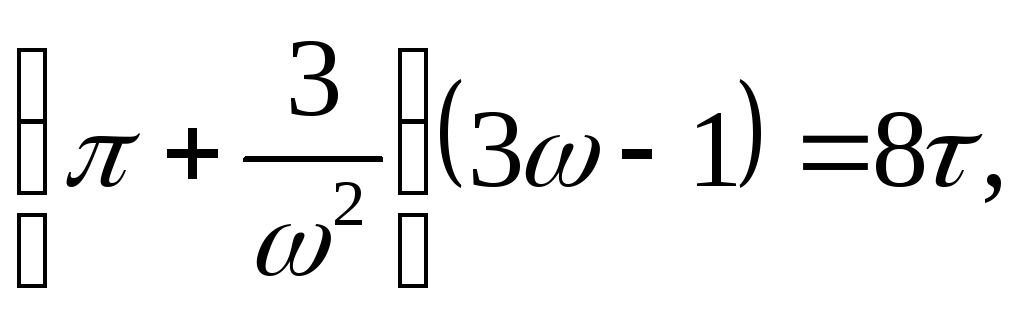 где
где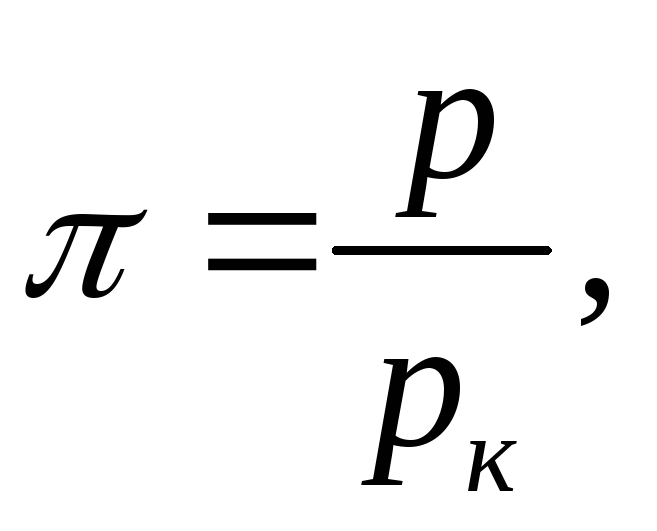
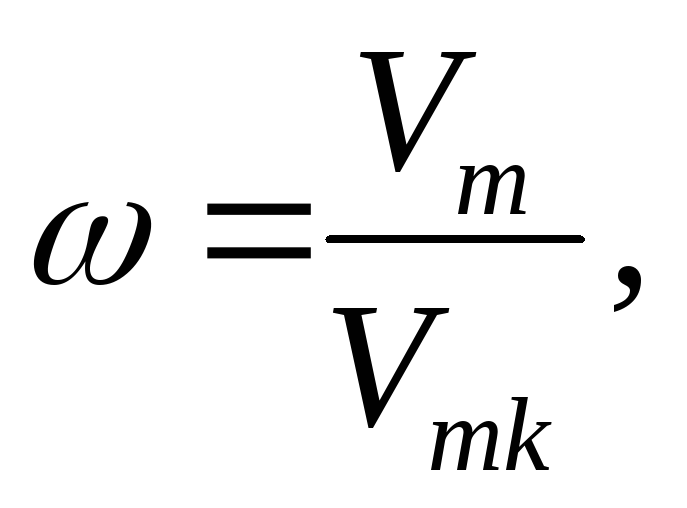
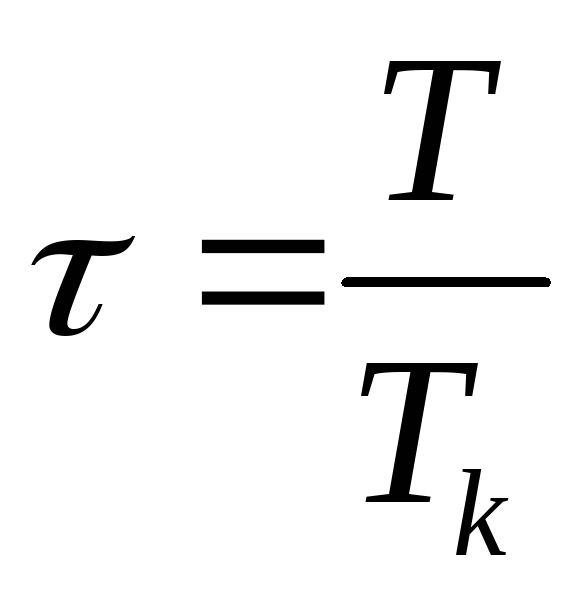 .
.Относительная влажность воздуха
 :
: ,
где
,
где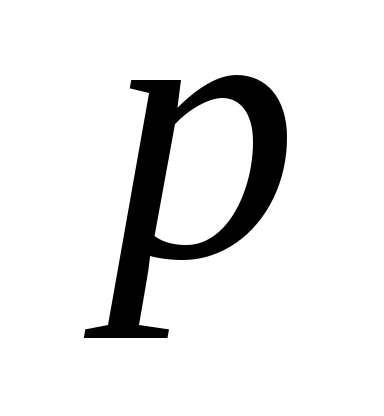 -
парциальное давление водяного пара,
находящегося в воздухе при данной
температуре (абсолютная влажность),
-
парциальное давление водяного пара,
находящегося в воздухе при данной
температуре (абсолютная влажность),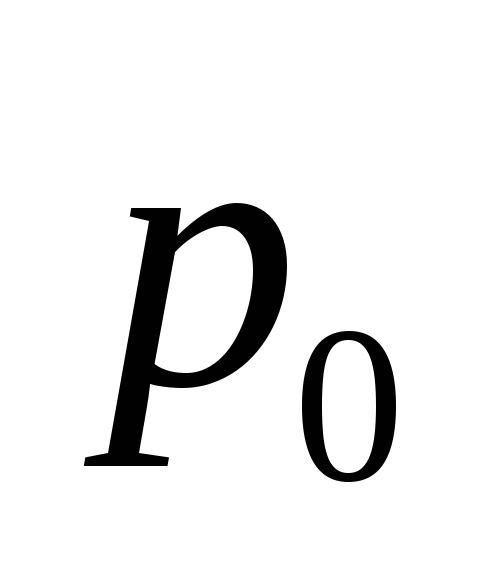 -
давление насыщенного пара при той же
температуре. Уравнение Клапейрона –
Клаузиуса:
-
давление насыщенного пара при той же
температуре. Уравнение Клапейрона –
Клаузиуса: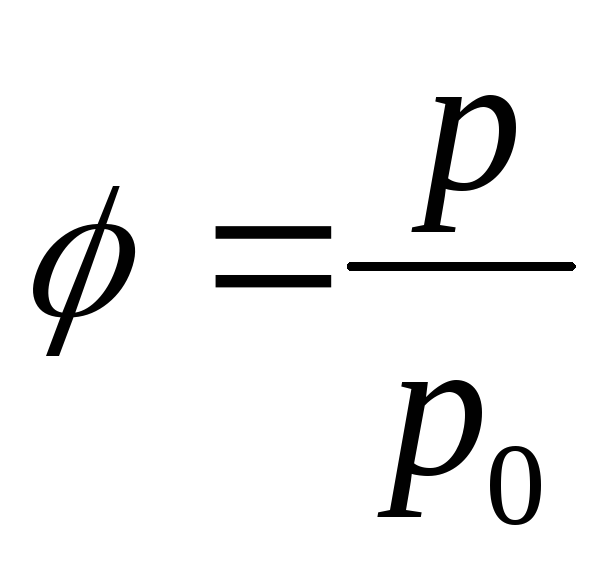 .
.Поверхностное натяжение:
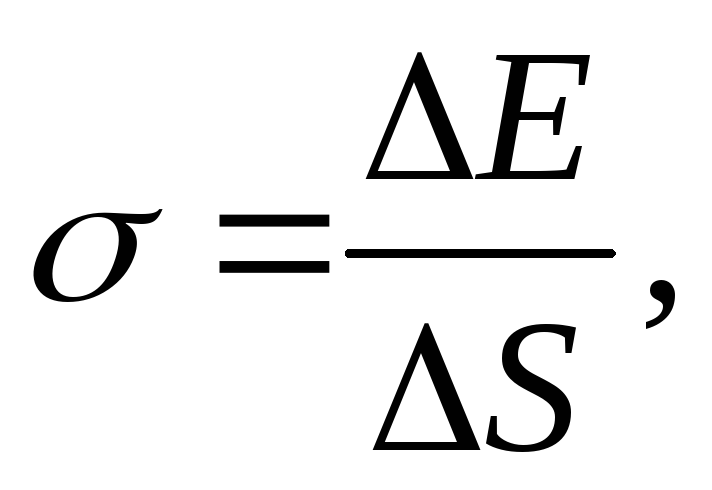 где
где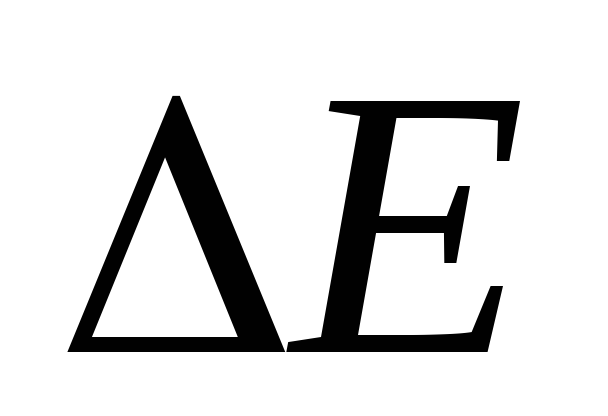 -
изменение свободной энергии поверхностного
слоя жидкости,
-
изменение свободной энергии поверхностного
слоя жидкости, -
изменение площади этого слоя.
-
изменение площади этого слоя.Добавочное давление, вызванное кривизной поверхности жидкости (формула Лапласа):
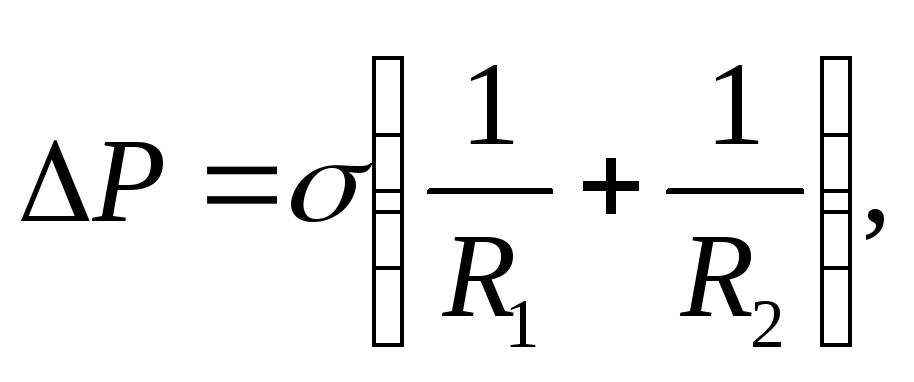 где
где и
и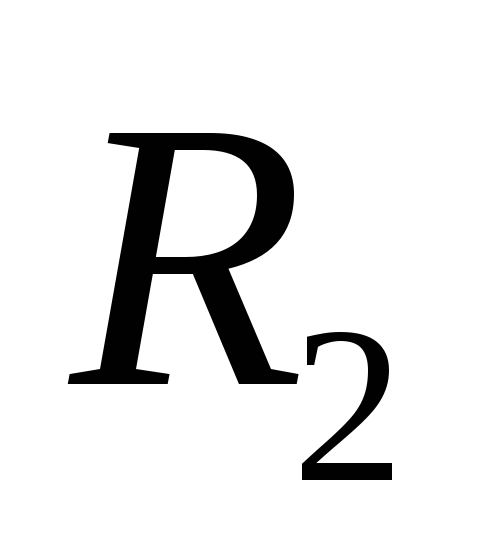 - радиусы кривизны двух взаимно
перпендикулярных сечений поверхности
жидкости.
- радиусы кривизны двух взаимно
перпендикулярных сечений поверхности
жидкости.Высота поднятия жидкости в капиллярных трубках:
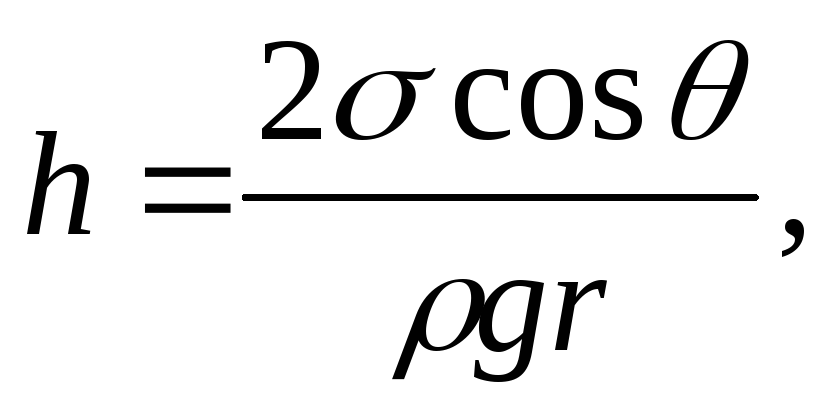
где
![]() -
краевой угол,
-
краевой угол,![]() -
плотность жидкости,
-
плотность жидкости,![]() -
радиус канала трубки.
-
радиус канала трубки.
Относительное изменение объема жидкости при нагревании:
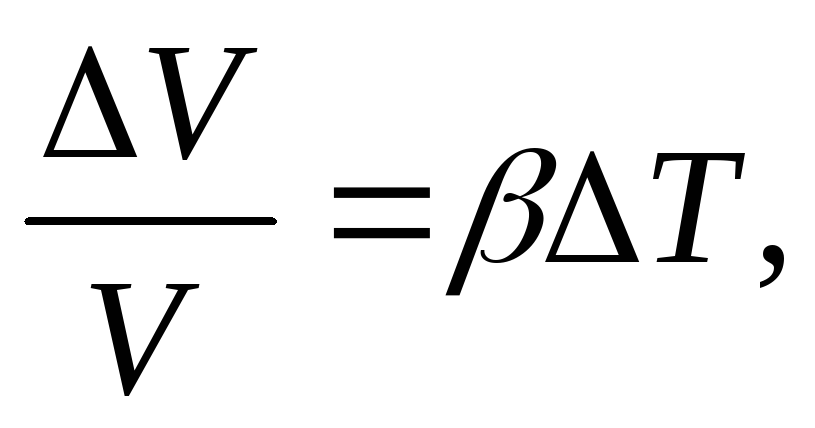 где
где -
температурный коэффициент объемного
расширения.
-
температурный коэффициент объемного
расширения.Относительное изменение объема жидкости при изменении давления:
![]() где
где
![]() - коэффициент сжатия. Плотность жидкости
при температуре
- коэффициент сжатия. Плотность жидкости
при температуре![]() :
:![]() где
где![]() -
плотность при
-
плотность при
![]() .
Осмотическое давление раствора (формула
Вант - Гоффа):
.
Осмотическое давление раствора (формула
Вант - Гоффа):![]() где
где![]() -
число молей растворенного вещества в
единице объема раствора.
-
число молей растворенного вещества в
единице объема раствора.
§ 6. Тепловые свойства твердых тел. Фазовые переходы.
Относительное изменение длины при изменении температуры на
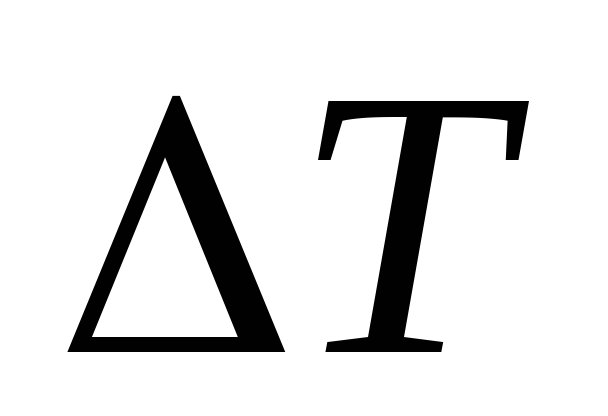 :
: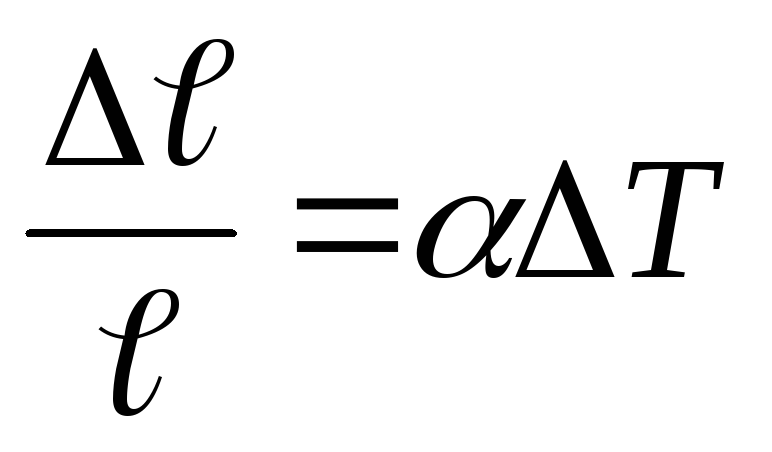 где
где -
начальная длина,
-
начальная длина, -
коэффициент линейного расширения.
-
коэффициент линейного расширения.Молярная теплоемкость химически простых твердых тел в классической теории теплоемкости (закон Дюлонга - Пти):

Примеры решения задач
Пример 1.
Подсчитать число молекул, содержащихся в 1 кг углекислого газа; найти массу одной молекулы. Вычислить для нормальных условий число молекул в 1 куб. м и в 1 куб. см газа и величину среднего расстояния между молекулами.
Решение.
Число
молекул в единице массы газа найдем из
соотношения:
![]() .
Тогда
.
Тогда![]()
![]() .
Число молекул в единице объема при
нормальных условиях равно
.
Число молекул в единице объема при
нормальных условиях равно
![]()
Для
массы одной молекулы имеем
![]() .
Среднее расстояние между молекулами в
газе составляет
.
Среднее расстояние между молекулами в
газе составляет![]() .
Подставляя в формулы числовые значения,
получим
.
Подставляя в формулы числовые значения,
получим![]()
![]() ,
в 1
,
в 1![]() молекул
в
молекул
в![]() раз меньше;
раз меньше;![]()
![]()
Ответ:
Число молекул в единице массы около
![]() ;
в единице объема примерно
;
в единице объема примерно![]() или
или![]() ;
масса молекулы
;
масса молекулы![]() приблизительно
приблизительно![]() ;
среднее расстояние между молекулами
газа при нормальных условиях около
;
среднее расстояние между молекулами
газа при нормальных условиях около
![]() .
.
Пример 2.
Найти
плотность кислорода при температуре
3000
Ки
давлении![]() .
Вычислить массу
.
Вычислить массу![]() кислорода при этих условиях.
кислорода при этих условиях.
Решение.
Задача решается с помощью уравнения
состояния газа
![]() и использованием формулы для плотности
вещества
и использованием формулы для плотности
вещества![]()
![]() .
Сделав подстановки и алгебраические
преобразования, получим
.
Сделав подстановки и алгебраические
преобразования, получим![]()
![]() .
Подставляя числовые значения, вычисляем
плотность кислорода при заданных
условиях:
.
Подставляя числовые значения, вычисляем
плотность кислорода при заданных
условиях:![]() ,
масса
,
масса![]() кислорода при тех же условиях равнаm=410
кг
кислорода при тех же условиях равнаm=410
кг
Задачу можно решить проще, применяя уравнение Менделеева – Клапейрона
![]() ,
откуда
,
откуда
![]()
![]()
Ответ:
Плотность кислорода при температуре
3000 К и давлении![]() равна
равна![]() ;
масса
;
масса![]() кислорода при этих условиях410кг.
кислорода при этих условиях410кг.
Пример 3.
Объем цилиндра поршневого насоса 0,50 л. Насос соединен с баллоном емкостью 3,0 л, содержащим воздух при нормальном атмосферном давлении. Найти давление воздуха в баллоне после 5 рабочих ходов поршня в случае нагнетательного и разрежающего режимов работы.
Решение.
1.
После nрабочих ходов
поршня в нагнетательном режиме насос
заберет из атмосферы объем воздуха![]() при давлении
при давлении![]() ;
эта масса воздуха будет введена в объем
баллона
;
эта масса воздуха будет введена в объем
баллона![]() ;
создав там парциальное давление
;
создав там парциальное давление![]() ;
так как изменения температуры не
учитывается, то по закону Бойля –
Мариотта
;
так как изменения температуры не
учитывается, то по закону Бойля –
Мариотта
![]() откуда
откуда
![]() .
Искомое давление воздуха в баллоне
будет равно
.
Искомое давление воздуха в баллоне
будет равно![]() .
Подставляя числовые значения, получим
.
Подставляя числовые значения, получим![]()
Ответ:
В нагнетательном режиме давление воздуха
в баллоне после 5 ходов поршня равно
![]() .
.
2.
В начале первого рабочего хода поршня
воздух в баллоне занимал объем
![]() при давлении
при давлении![]() .
К концу первого хода поршня та же масса
воздуха займет объем
.
К концу первого хода поршня та же масса
воздуха займет объем![]() при давлении
при давлении![]() .
Так как изменение температуры не
учитывается, то по закону Бойля-Мариотта
.
Так как изменение температуры не
учитывается, то по закону Бойля-Мариотта![]()
![]() .
В начале второго хода поршня объем и
давление газа в баллоне равны соответственно
.
В начале второго хода поршня объем и
давление газа в баллоне равны соответственно![]() и
и![]() ;
в конце хода они равны
;
в конце хода они равны![]() и
и![]() .
Отсюда
.
Отсюда![]() или
или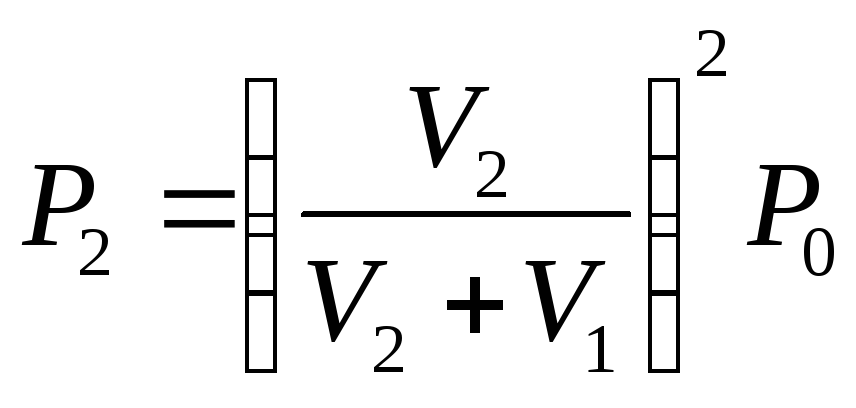 .
Продолжая те же рассуждения, находим,
что к концуn-го рабочего
хода
.
Продолжая те же рассуждения, находим,
что к концуn-го рабочего
хода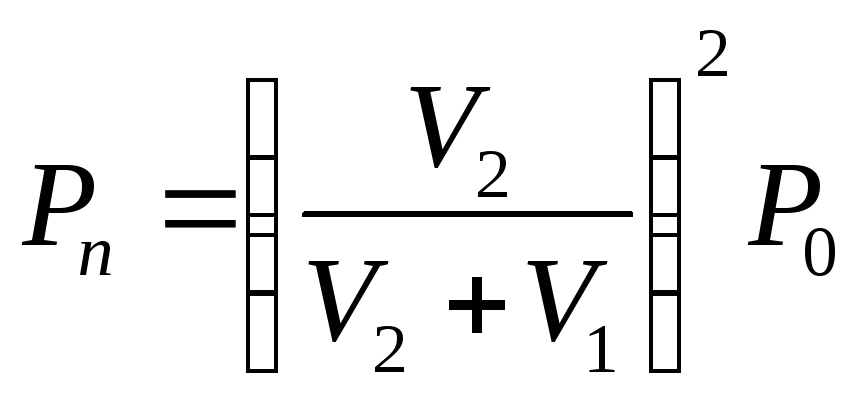 .
Подставляя числовые значения, получим
.
Подставляя числовые значения, получим![]()
![]()
![]()
![]()
Ответ.
В разрежающем режиме давление воздуха
в сосуде после 5 ходов поршня равно![]() .
.
Пример 4.
Стальной снаряд летевший со скоростью 200 м/с, ударяется в земляную насыпь и застревает в ней. На сколько градусов повысится температура снаряда, если на его нагревание пошло 60% кинетической энергии?
Решение.
Из всей кинетической энергии снаряда
на его нагревание ушла часть энергии
![]() .
Увеличение внутренней энергии снаряда
равно
.
Увеличение внутренней энергии снаряда
равно![]() .
Составим уравнение теплового баланса:
.
Составим уравнение теплового баланса:![]()
Из
составленного уравнения теплового
баланса находим
![]() .
Подставляя числовые значения, получим
.
Подставляя числовые значения, получим![]()
Ответ: Температура снаряда повысилась примерно на 26 0 К.
Пример 5.
На сколько километров пути хватит автомобилю 40л бензина, если вес автомашины 3,6 т, общее сопротивление движению составляет 0,050 веса, к.п.д. двигателя 18%. Движение считать равномерным.
Решение.
Пройденный путь можно найти из формулы
для работы, совершенной двигателем:
![]() .
Работу
.
Работу![]() двигатель совершает, используя часть
двигатель совершает, используя часть![]() всей энергии
всей энергии![]() ,
полученной при сжигании топлива:
,
полученной при сжигании топлива:![]() ,
откуда
,
откуда![]() .
Энергия, выделяющаяся при сгорании
топлива, равна
.
Энергия, выделяющаяся при сгорании
топлива, равна![]() ¸где
¸где![]()
Отсюда
![]()
Cила
тяги при равномерном движении равна
силе сопротивления движению![]() ,
которая по условию составляет 0,050 веса
машины, т.е.
,
которая по условию составляет 0,050 веса
машины, т.е.![]() .
Полученные нами выражения дляA
иFподставляем в
формулу дляS
.
Полученные нами выражения дляA
иFподставляем в
формулу дляS ![]()
Подставляя
числовые значения и вычисления, получаем:
![]()
Ответ: Бензина хватит на 130 км.
Пример 6.
На
электроплитке мощностью 600 Вт за 35 мин
нагрели 2,0 л воды от 2930 до 3730![]() ,
причем 200 г воды обратилось в пар.
Определить к.п.д. электроплитки.
,
причем 200 г воды обратилось в пар.
Определить к.п.д. электроплитки.
Решение.
По определению к.п.д. нагревателя равен
![]() ,
где
,
где![]() –
количество тепла, израсходованное на
нагрев воды и на превращение части воды
в пар.
–
количество тепла, израсходованное на
нагрев воды и на превращение части воды
в пар.![]() –
энергия, израсходованная электроплиткой.
–
энергия, израсходованная электроплиткой.
Подставим
выражение для Q 1
иQ 2в формулу для к.п.д.![]() .
.
Подставляя
числовые значения, получаем:
![]()
Ответ. Коэффициент полезного действия электроплитки приблизительно равен 89%.
Пример 7.
На какую высоту поднимается вода в стеклянном капилляре диаметром 0,20 мм? Краевой угол считать равным 30ºС, а температуру 288 0К.
Решение.
Высота подъема или опускания жидкости
в капилляре определяется по формуле
-
![]() , мениск имеет в этом случае форму
сферического сегмента.
, мениск имеет в этом случае форму
сферического сегмента.
(Если
же мы будем считать, что жидкость вполне
смачивает или вполне не смачивает стенки
капилляра, то мениск будет представлять
собой полусферу; значение краевого угла
будет соответственно равно нулю для
смачивания или 180º для не смачивания,
формула для
![]() примет вид
примет вид![]() ).
Подставив в формулу для
).
Подставив в формулу для![]() числовые значения, получим
числовые значения, получим![]()
Ответ. Высота подъема воды в капилляре равна примерно 12,7 см.
Пример 8.
В стеклянный сосуд массой 1,5 кг, содержащий 4,2 кг воды при температуре
333 0К, опускают 1,5 кг льда при температуре 2330К. Определить окончательную температуру воды.
Решение.
Задача решается с помощью уравнения
теплового баланса. Допустим, что весь
лед растает в горячей воде; тогда
количество тепла, полученное льдом и
образовавшейся из него водой, будет
равно
![]()
Количество тепла, отданное водой в сосуде при ее охлаждении от T1 доQ, равно
![]() .
.
На
основании закона сохранения энергии
составляем уравнение теплового баланса
![]() или
или![]()
Решение.
Решив уравнение теплового баланса
относительно![]() ,
найдем.
,
найдем.
![]() .
Подставляя числовые значения, получим
.
Подставляя числовые значения, получим
![]()
Ответ: Окончательная температура воды в сосуде равна 293 0К.
Пример 9.
При 0ºС стеклянная колба вмещает 680 г ртути, а при 100ºС – 670 г ртути. Определить коэффициент линейного расширения стекла.
Решение.
Коэффициент линейного расширения стекла
![]() ,причем
,причем![]() можно найти из соотношения
можно найти из соотношения![]() .
Где
.
Где![]() и
и![]() -
объемы колбы и заполняющей колбу ртути
при соответствующих температурах. Масса
ртути, занимающей объем
-
объемы колбы и заполняющей колбу ртути
при соответствующих температурах. Масса
ртути, занимающей объем![]() ,
равна
,
равна![]() ,
причем
,
причем![]() Масса ртути, занимающая объем
Масса ртути, занимающая объем![]() ,
равна
,
равна![]() .
Возьмем отношение массmиmo.
Найдем значение
.
Возьмем отношение массmиmo.
Найдем значение![]()
Разделив
mнаm0,
получим![]()
Найдем
![]()
![]()
Подставляя
числовые значения, получим
![]()
Ответ:
Коэффициент линейного расширения стекла
примерно равен 1·10-5 ![]()
