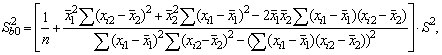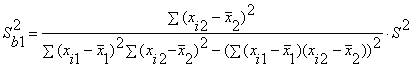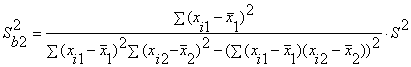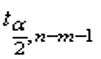Двумерное уравнение регрессии пр3 вар16 — копия
.docxФГБОУ ВО
«Уфимский государственный авиационный технический университет»
Кафедра ТК
ОТЧЕТ
по практической работе №3
по дисциплине “Всеобщее управление качеством”
Двумерное уравнение регрессии
Вариант 16
Проверил: проф.
Гвоздев В. Е.
Цель работы: Изучение методов построения моделей многомерных объектов на основе измерительных данных.
Задание на работу:
Оценить на основе совместно зарегистрированных значенийX1, X2 и Y параметры двумерной линейной регрессии . Номер варианта соответствует номеру в групповом журнале.
Вычислить интервальные оценки параметров линейной двухмерной регрессии.
Ход работы:
Часть первая
-
№Набл.
x
y
z
1
35,6898
22,0033
32,7950
2
4,7878
47,9330
13,6963
3
103,7932
12,0682
8,9156
4
80,1675
23,6622
-6,9500
5
110,0537
15,9769
-1,6031
6
115,3846
56,8871
12,2153
7
101,7379
0,4095
12,7538
8
102,1299
-11,4236
23,4583
9
-15,1056
23,2715
17,0727
10
38,7043
40,4842
29,3443
11
86,7936
59,0597
12,6149
12
62,4481
39,4466
13,4281
13
57,2195
-1,3262
27,2829
14
-67,0386
5,2566
14,3718
15
16,8304
14,6874
32,7934
16
-16,8660
60,3074
24,8202
17
25,3091
40,1323
31,8389
18
-31,8195
29,8299
-25,1961
19
52,1658
9,8169
13,5294
20
32,6892
61,1272
-27,8764
|
|
|
|
|
|
|
|
19,83 |
393,22 |
-5,48 |
30,00 |
-9,06 |
-179,73 |
-108,61 |
49,64 |
0,73 |
0,53 |
20,45 |
418,31 |
-39,97 |
-29,22 |
14,95 |
-817,40 |
-4,05 |
16,40 |
-15,41 |
237,54 |
59,04 |
-239,09 |
62,41 |
-909,93 |
-19,92 |
396,62 |
-3,82 |
14,58 |
35,41 |
-705,28 |
76,04 |
-135,22 |
-14,57 |
212,24 |
-11,50 |
132,33 |
65,30 |
-951,31 |
167,59 |
-751,19 |
-0,75 |
0,56 |
29,41 |
864,75 |
70,63 |
-52,97 |
-22,05 |
2077,01 |
-0,21 |
0,04 |
-27,07 |
732,84 |
56,98 |
-12,05 |
5,72 |
-1542,62 |
10,49 |
110,10 |
-38,90 |
1513,53 |
57,38 |
602,05 |
-408,22 |
-2232,17 |
4,11 |
16,87 |
-4,21 |
17,72 |
-59,86 |
-245,87 |
-17,29 |
251,95 |
16,38 |
268,27 |
13,00 |
169,10 |
-6,05 |
-99,08 |
212,99 |
-78,67 |
-0,35 |
0,12 |
31,58 |
997,25 |
42,04 |
-14,73 |
-11,06 |
1327,59 |
0,46 |
0,21 |
11,97 |
143,19 |
17,69 |
8,19 |
5,54 |
211,73 |
14,32 |
205,00 |
-28,81 |
829,82 |
12,47 |
178,48 |
-412,44 |
-359,10 |
1,41 |
1,98 |
-22,22 |
493,90 |
-111,79 |
-157,24 |
-31,26 |
2484,46 |
19,83 |
393,15 |
-12,79 |
163,66 |
-27,92 |
-553,67 |
-253,66 |
357,23 |
11,85 |
140,54 |
32,83 |
1077,60 |
-61,62 |
-730,50 |
389,16 |
-2022,78 |
18,87 |
356,21 |
12,65 |
160,07 |
-19,44 |
-366,99 |
238,79 |
-246,01 |
-38,16 |
1456,29 |
2,35 |
5,52 |
-76,57 |
2922,14 |
-89,66 |
-179,90 |
0,56 |
0,32 |
-17,66 |
312,00 |
7,41 |
4,18 |
-9,96 |
-130,92 |
-40,84 |
1668,04 |
33,65 |
1132,10 |
-12,06 |
492,73 |
-1374,19 |
-405,93 |
-
x
y
z
МИН
-27,8764
-11,4236
-67,0386
МАКС
32,7950
61,1272
115,3846
среднее
12,9653
27,4805
44,7537
b2
b1
b0
Коэффициенты регрессии
-27,8764
-11,4236
-67,0386
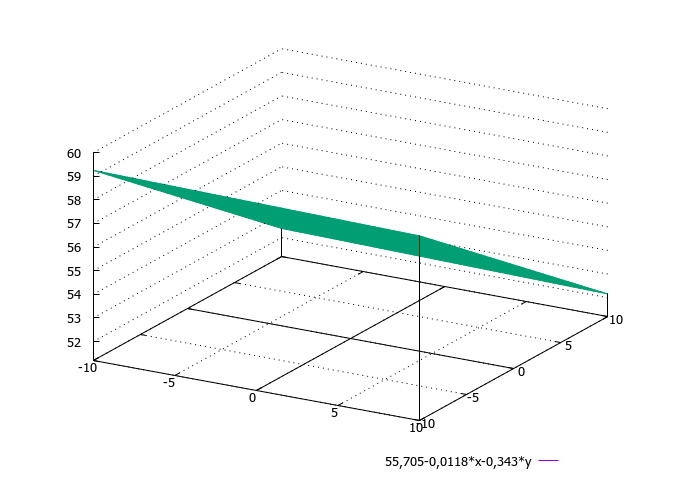
Регрессионная модель: Z=55,705-0,0118*Х1-0,343*Х2
Спрашивал за циферки, как я поняла 55,705 это цифра показывающая степень влияния неучтенных параметров, 0,0118 – степень влияния параметра Х1, 0,343 – степень влияния параметра Х2 соответственно. И вся эта функция показывает, что неучтенные нами параметры имеют гораздо большее влияние, чем те, которые мы рассматриваем.
-
Z
Zm
32,7950
14,0090
13,6963
9,9953
8,9156
14,8400
-6,9500
13,1685
-1,6031
14,0977
12,2153
7,0856
12,7538
16,8450
23,4583
18,8489
17,0727
14,4319
29,3443
10,8337
12,6149
7,0760
13,4281
10,7115
27,2829
17,6990
14,3718
18,1427
32,7934
15,4879
24,8202
8,1666
31,8389
11,0618
-25,1961
13,5285
13,5294
15,8708
-27,8764
7,4048
Часть вторая
Регрессионная модель: Z=55,705-0,0118*Х1-0,343*Х2
|

|
Интервал при b0 |
Интервал при b1 |
Интервал при b2 |
от |
5,7236 |
-1,6934 |
-1,5596 |
до |
105,6858 |
1,4569 |
0,8742 |
спрашивал за выделенные штуки, что значат, зачем нужны.
Вывод: В ходе данной практической работы были оценены параметры двумерной линейной регрессии на основе совместно зарегистрированных значений X1, X2 и Y, вычислены интервальные оценки параметров линейной двухмерной регрессии.