Вычисление показателей параметрической надежности по характеристикам случайных процессов изменения определяющих параметров вар — копия
.docxСпрашивал зачем мы оставляли выпадающие значения, и по сути их можно в табличку не включать
Значения нормирующего множителя с, параметров нормального закона распределения {
}
и вероятности
нахождения в работоспособном состоянии
в каждом временном сечении:
Значение нормирующего множителя с находим по формуле:
,
где
,
.
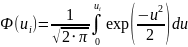Значение вероятности
нахождения в работоспособном состоянии
находим по формуле
,
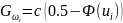где
,
.
Таблица 5 – Значения вероятности нахождения в работоспособном состоянии
t |
|
с* |
m |
σ |
0 |
0,96 |
1 |
8,87 |
5,11 |
1 |
0,88 |
1 |
5,86 |
4,88 |
2 |
0,94 |
1 |
6,67 |
4,32 |
3 |
0,89 |
1 |
6,39 |
5,15 |
4 |
0,88 |
1 |
6,41 |
5,45 |
5 |
0,94 |
1 |
7,46 |
4,80 |
6 |
0,92 |
1 |
7,24 |
5,12 |
7 |
0,95 |
1 |
8,17 |
5,03 |
8 |
0,94 |
1 |
8,33 |
5,31 |
9 |
0,97 |
1 |
9,13 |
4,97 |
10 |
0,96 |
1 |
9,05 |
5,11 |
11 |
0,98 |
1 |
9,49 |
4,62 |
12 |
0,98 |
1 |
9,43 |
4,69 |
13 |
0,98 |
1 |
9,37 |
4,77 |
14 |
0,97 |
1 |
9,31 |
4,86 |
*Параметр с равен 1, потому что границы фактически возможных значений не достигаются
Вычисление плотности распределения наработки до параметрического отказа
Вот это вроде не нужно было.
По данным из таблицы
3 рассчитал математическое ожидание и
среднеквадратическое отклонение
,
.
=0,06
=0,03
-
t
f
0
0,31
1
0,97
2
0,53
3
0,94
4
0,97
5
0,53
6
0,75
7
0,41
8
0,53
9
0,21
10
0,31
11
0,14
12
0,14
13
0,14
14
0,21
Вот это я пересчитывала на месте, уже не помню что там было не так, но график в итоге получился очень схожий, вопросы по графику задавал кста.
П
о
полученным данным была построена
гистограмма плотности распределения
наработки до параметрического отказа:
Рисунок 1 – Гистограмма плотности распределения наработки до параметрического отказа
Вывод: В ходе данной лабораторной работы были вычислены показатели параметрической надежности по характеристикам случайных процессов изменения определяющих параметров.