лр4 вариант17 (Построение классификационных шкал с учетом статистических особенностей данных) — копия

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра технической кибернетики

ОТЧЕТ

по лабораторной работе №4.

по дисциплине «Моделирование»

«Построение классификационных шкал с учетом статистических особенностей данных»

Проверил:

Гвоздев В. Е.

Вариант 17

Цель работы: Изучение методики классификации объектов по выборочным данным показателей состояния.

Задание: По данным, приведенным в Таблице 1, построить классификационную шкалу и осуществить одноуровневую классификацию объектов.

Таблица 1

Номер измерения	Значение показателя состояния
1	90
2	79
3	87
4	77
5	39
6	95
7	5
8	71
9	64
10	71

а) Расчет характеристик эмпирической функции распределения

Шаг 1. Выборочные данные преобразуется к виду , где a – левая граница физически возможных значений случайной величины Z_i (в общем случае а может принимать нулевое значение).

Таблица 2

Номер измерения
1	85
2	74
3	82
4	72
5	34
6	90
7	0
8	66
9	59
10	66

Шаг 2. По значениям рассчитываются эмпирические значения матожидания 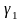и среднеквадратического отклонения

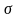
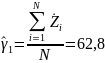
Шаг 3. по значениям , рассчитывается идентификатор формы эмпирической функции распределения

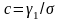
б) Определение числа классов

Шаг 4. По рассчитанному значению идентификатора формы эмпирической функции распределения и заданному объему выборки N на основании таблицы 1 определяется число классов состояния n_опт.

n_опт = 2.

в) Построение оценки эмпирической функции распределения и формирование классификационной шкалы

Шаг 5. Осуществляется построение оценки эмпирической функции распределения. Для этого исходные выборочные значения 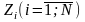ранжируются в порядке возрастания, т.е. на базе формируется вариационный ряд , после чего осуществляются преобразования вида

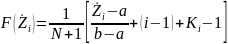
где 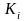- число одинаковых значений .

a-минимальное значение ;

b-максимальное значение .

Таблица 3

	F(z)
5	0,00
39	0,13
64	0,24
71	0,43
71	0,52
77	0,53
79	0,62
87	0,72
90	0,81
95	0,91

Шаг 6. По построенной оценке 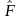(Z) с учетом полученного на шаге 4 значения n_опт строится классификационная шкала.

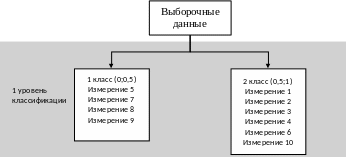
По какой оси определяются границы классов состояний??

По вертикальной если шо.

Рисунок 1 – Классификационная шкала

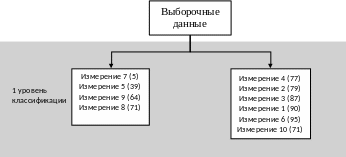
Рисунок 2 – Одномерная классификация

Вывод: В ходе данной лабораторной работы были изучены методы классификации объектов по выборочным показателям состояния. По данным, приведенным в Таблица 1, были построены классификационная шкала и осуществленная одноуровневая классификация объектов.

Ответы на контрольные вопросы:

1. Чем обусловлена необходимость решения задачи классификации с точки зрения управления сложными объектами?

Необходимость решения задачи классификации с точки зрения управления сложными объектами обусловлена тем, что классификации объектов по выборочным данным показателей состояния позволяет применять к объектам одного класса схожие методы и принципы действий, что значительно упрощает управление сложным объектом.

2. Чем обусловлена необходимость решения задачи классификации при малом числе исходных данных?

Необходимость заключается в том, что из-за малого количества исходных данных появляется недостаток информации. Классификация позволяет выделить основные схожие черты объектов, что упрощает работу с ними.

Операция агрегирования (к которой относится также и классификация) приводит к потере информации. Если данных мало, то зачем еще терять информацию?

3. Дайте описание ограниченной методике?

Данный метод может использоваться только для объектов, имеющих количественные характеристики (измеренные в некоторой количественной шкале).

Почему тогда нельзя использовать ХИ-квадрат, либо F-кпитерий Колмогорова?

4-

тут дядя опять до вопросов доебался, это его любимое