
- •Часть 1
- •8.337 (Округлить до десятых) ≈ 8.3; 833.438 (округлить до целых) ≈ 833; 0.27375 (округлить до сотых) ≈ 0.27.
- •8.3351 (Округлить дл сотых) ≈ 8.34; 0.2510 (округлитьь до десятых) ≈ 0.3; 271.515 (округлить до целых) ≈ 272.
- •1. Определение плотности вещества для тел правильной геометрической формы
- •2. Определение ускорения свободного падения с помощью физического маятника
- •3. Определение момента инерции диска относительно оси симметрии методом наклонной плоскости
- •4. Определение момента инерции тела методом колебаний
- •5. Определение модуля юнга кости животного
- •6. Изучение спектральной характеристики уха человека
- •5. Повторите измерения на других частотах. Результаты запишите в таблицу:
- •7. Определение коэффициента вязкости жидкости методом стокса
- •8. Определение расхода воды методом водомера вентури
- •9. Определение влажности воздуха с помощью аспирационного психрометра
- •394087, Г. Воронеж, ул. Мичурина, 1
8. Определение расхода воды методом водомера вентури
Цель работы: изучение законов течения идеальной жидкости
Приборы и оборудование: экспериментальная установка (водомер Вентури), секундомер, весы, разновес
Теоретическая часть
Идеальной называется воображаемая абсолютно несжимаемая жидкость, не обладающая вязкостью. Ряд реальных жидкостей (ацетон, спирт, бензин, вода, эфиры) обладают свойствами, близкими к идеальной жидкости. В частности, вода практически несжимаема, ее вязкость мала, и ее можно приближенно считать идеальной жидкостью.
Если движение жидкости ламинарное (слои движутся параллельно и не перемешиваются), то можно ввести понятие линий тока. Линия тока - линия, касательная к которой в каждой точке совпадает с вектором скорости движения жидкости. Часть пространства, ограниченная со всех сторон линиями тока, называется трубкой тока.
Для несжимаемой жидкости справедлива теорема о неразрывности струи: для любого поперечного сечения трубки тока произведение площади поперечного сечения S на скорость движения v есть величина постоянная.
![]()
Произведение S на v имеет физический смысл расхода жидкости Q - объема жидкости, проходящей через поперечное сечение трубки тока за единицу времени.
Для течения идеальной жидкости справедливо уравнение Бернулли:
![]()
Здесь - плотность жидкости, g – ускорение свободного падения, h – расстояние от середины сечения трубки тока до горизонтальной поверхности, v – скорость течения.
Р
– статическое давление жидкости, gh
–
гидростатическое давление,
![]() - динамическое давление.
- динамическое давление.
Согласно закону Бернулли для любого поперечного сечения трубки тока сумма динамического, гидравлического и статического давлений есть величина постоянная.

Если
трубка расположена горизонтально, то
h1=h2
, gh1=gh2
![]()
При
![]() получаем
получаем
![]() ,
и равенство выполняется, если
,
и равенство выполняется, если
![]() .
То есть, там,
где скорость течения жидкости больше,
статическое давление меньше.
Кровь является вязкой жидкостью, и для
нее нельзя вести строгие расчеты с
использованием уравнения Бернулли. Но
качественные закономерности, следующие
из данного уравнения, справедливы и
для крови. При течении крови по артериям
скорость движения у стенок меньше.
Поэтому форменные элементы (лейкоциты,
тромбоциты, эритроциты) группируются
преимущественно в средней части артерии.
.
То есть, там,
где скорость течения жидкости больше,
статическое давление меньше.
Кровь является вязкой жидкостью, и для
нее нельзя вести строгие расчеты с
использованием уравнения Бернулли. Но
качественные закономерности, следующие
из данного уравнения, справедливы и
для крови. При течении крови по артериям
скорость движения у стенок меньше.
Поэтому форменные элементы (лейкоциты,
тромбоциты, эритроциты) группируются
преимущественно в средней части артерии.
Движение
жидкости может быть не только ламинарным,
но и турбулентным.
В этом случае течение не является
стационарным, оно перестает быть
слоистым, скорости молекул жидкости в
каждой точке меняются, возникают
завихрения и шумы. О характере потока
можно судить, например, по величине
числа
Рейнольдса
![]() , где D –
диаметр трубы (сосуда),
- коэффициент вязкости жидкости. Для
крови при Re
2000 ее течение будет ламинарным, при Re
3000 - турбулентным.
, где D –
диаметр трубы (сосуда),
- коэффициент вязкости жидкости. Для
крови при Re
2000 ее течение будет ламинарным, при Re
3000 - турбулентным.
Расход
жидкости, в частности – крови, может
быть найден по формуле Пуазейля:
![]() , где
, где
![]() - гидравлическое
сопротивление
сосуда, r
– радиус кровеносного сосуда, Р
– разность давлений на участке сосуда
длиной l.
- гидравлическое
сопротивление
сосуда, r
– радиус кровеносного сосуда, Р
– разность давлений на участке сосуда
длиной l.
При последовательном соединении сосудов с гидравлическими сопротивлениями Z1 и Z2 общее гидравлическое сопротивление Z = Z1 + Z2.
При
параллельном соединении сосудов
![]() .
.
Из
формулы Пуазейля следует, что
![]() ,
и падение давления в сосуде определяется
расходом крови и гидравлическим
сопротивлением сосуда. Падение давления
очень мало в аорте, так как ее радиус
велик и Z
мало. В других артериях радиус сосудов
меньше, гидравлическое сопротивление
и падение давления значительно больше.
В капиллярах падение давления мало,
так как несмотря на очень большое
гидравлическое сопротивление расход
крови чрезвычайно мал.
,
и падение давления в сосуде определяется
расходом крови и гидравлическим
сопротивлением сосуда. Падение давления
очень мало в аорте, так как ее радиус
велик и Z
мало. В других артериях радиус сосудов
меньше, гидравлическое сопротивление
и падение давления значительно больше.
В капиллярах падение давления мало,
так как несмотря на очень большое
гидравлическое сопротивление расход
крови чрезвычайно мал.
Порядок выполнения работы
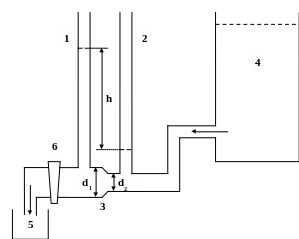
В настоящей работе определяется расход воды с помощью водомера Вентури, в котором имеются две трубки манометра (1 и 2), соединенные широким (диаметром d1) и узким (диаметром d2) сечениями трубки 3, по которой вода из резервуара 4 выливается в сосуд 5. Расход жидкости регулируется краном 6.
В
данном случае расход воды можно
рассчитать по формуле
![]() ,
,
где
![]() и
и
![]() ,
,
d1 = 810-3 м, d2 = 1,910-3 м, h – разность уровней воды в трубках 1 и 2 при открытом кране 6.
Тот же расход воды можно определить весовым методом с использованием формулы
![]()
,
где m1 –
масса сосуда 5 без воды, m2
– масса того же сосуда с водой, t
– время, за которое наполняется сосуд
5, - плотность
воды (
![]() ).
).
Путем взвешивания найдите массу m1 пустого сосуда 5.
Поставьте сосуд 5 под кран 6, откройте кран и одновременно включите секундомер, измерьте во время течения воды разность уровней h в манометре, через 20 – 30 сек. закройте кран.
Определите m2 сосуда 5 с водой.
По рабочим формулам вычислить расход воды Q1 и Q2 (при вычислениях все величины выразить в СИ)
Контрольные вопросы и задания
Ламинарное и турбулентное движение жидкости. Число Рейнольдса. Линии тока, трубки тока.
Теорема о неразрывности струи, уравнение Бернулли. Почему форменные элементы крови группируются в средней части артерии?
Расход жидкости. Формула Пуазейля, гидравлическое сопротивление.
От чего зависит падение давления крови в кровеносных сосудах? Почему падение давления в аорте и капиллярах меньше, чем в артериях? Как сказывается сужение артерий при чуме на расходе крови?
