Примеры тестовых вопросов по теории вероятностей и математической статистике

1. Бросают 2 монеты. События {на первой монете выпадет герб} и {на второй монете выпадет цифра} являются (выберите правильные утверждения): 1) совместными; 2) несовместными; 3) зависимыми; 4) независимыми.

2. В урне находятся 1 белый и 2 черных шара. Из урны поочередно вынимают два шара, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются. Тогда вероятность того, что оба шара белые, равна …

3. Игральная кость бросается один раз. Тогда вероятность того, что на ее верхней грани выпадет не менее пяти очков, равна…

4. Пусть попарно независимые события, причем , . Найдите .

5. В урне 6 белых и 4 черных шара. Наудачу одновременно берут два шара. Какова вероятность, что оба они белые?

6. В лотерее 1 000 билетов. Выигрыш 5000 рублей выпадает на один билет, выигрыш по 1 000 рублей – на десять билетов, выигрыш по 200 рублей – на пятьдесят билетов, выигрыш по 50 рублей – на сто билетов; остальные билеты – без выигрыша. Покупается один билет. Тогда вероятность выигрыша не менее 50 рублей, но не более 200 рублей равна…

7. Образуют ли несовместные события полную группу, если ? Почему?

8. В первой урне 4 черных и 6 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…

9. В первой урне 4 черных и 6 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар, который оказался белым. Тогда вероятность того, что этот шар извлечен из первой урны, равна…

10. В урне из 10 шаров имеется 6 красных. Наудачу берут два шара. Тогда вероятность того, что среди них только один красный, равна…

11. Случайные события , удовлетворяющие условиям , являются (выберите правильные утверждения): 1) совместными; 2) несовместными; 3) зависимыми; 4) независимыми.

12. Случайные события , удовлетворяющие условиям , являются (выберите правильные утверждения): 1) совместными; 2) несовместными; 3) зависимыми; 4) независимыми.

13. Игральная кость брошена три раза. Какова вероятность того, что при этом хотя бы раз выпадет число, кратное трем?

14. Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелка равны соответственно 0,7 и 0,8. 1) Какова вероятность того, что в цель попадет только один стрелок? 2) Какова вероятность того, что цель будет поражена?

15. Страхуется 2500 автомобилей. Считается, что каждый из них может попасть в аварию с вероятностью 0,09. Для вычисления вероятности того, что количество аварий среди всех застрахованных автомобилей не превзойдет 230, следует использовать (выберите правильное утверждение): 1) формулу Пуассона; 2) формулу Бейеса; 3) интегральную формулу Муавра-Лапласа; 4) формулу полной вероятности.

16. Пусть X – дискретная случайная величина, заданная законом распределения вероятностей вида

X
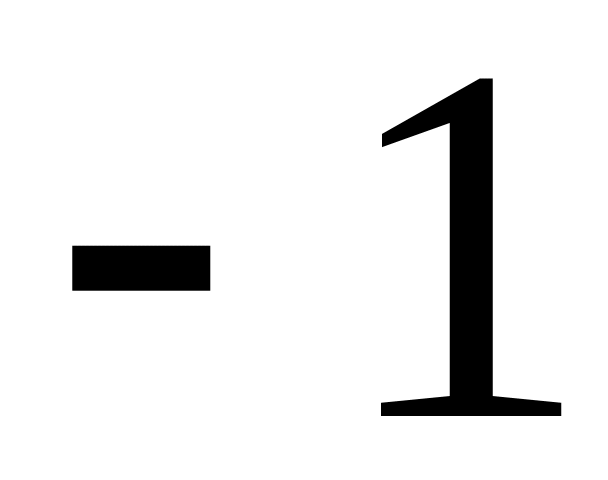
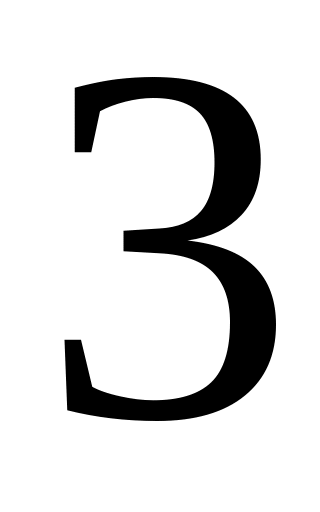
p	0,7	0,3

Тогда: 1) математическое ожидание этой случайной величины равно…; 2) математическое ожидание случайной величины равно…; 3) значение интегральной функции распределения вероятностей равно…

17. Пусть X – дискретная случайная величина, заданная законом распределения вероятностей вида

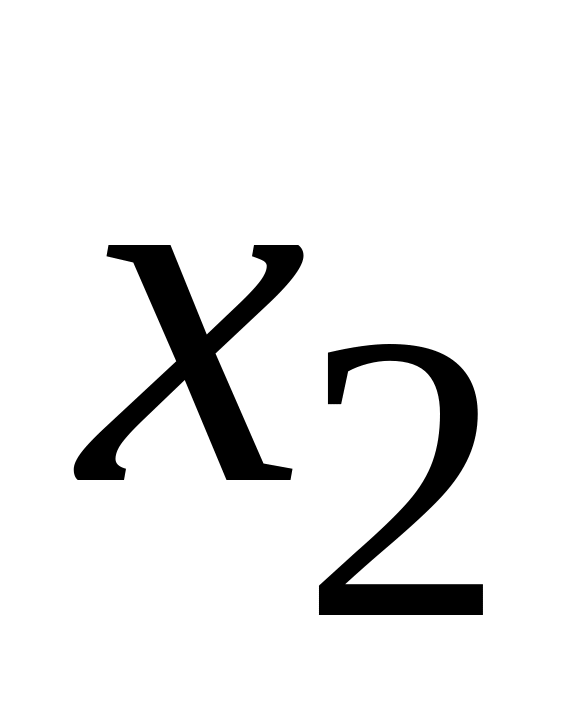
X	0		9
p	0,1	0,5

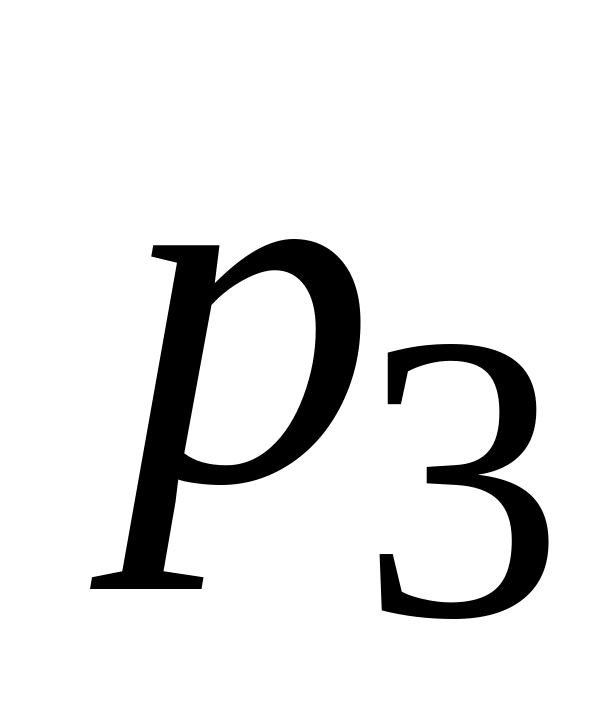
c . 1) Чему равно значение ? 2) Чему равно значение ?

18. Вероятность появления некоторого события в каждом из 30 независимых испытаний, проводимых по схеме Бернулли, равна 0,8. Чему равны математическое ожидание и дисперсия числа появлений этого события в испытаниях?

19. Случайная величина Х задана плотностью распределения вероятностей следующего вида:

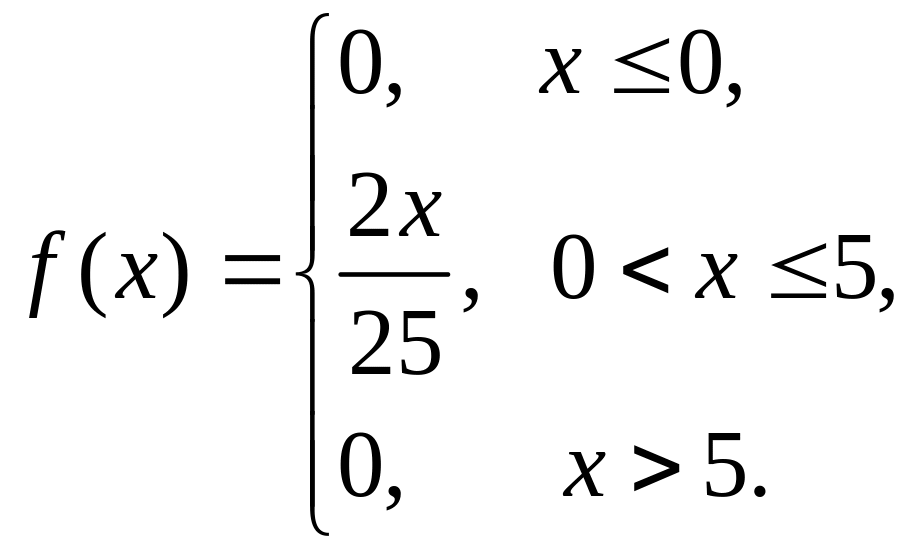
Тогда соответствующая функция распределения вероятностей равна…

20. Непрерывная случайная величина Х задана следующей интегральной функцией распределения вероятностей:

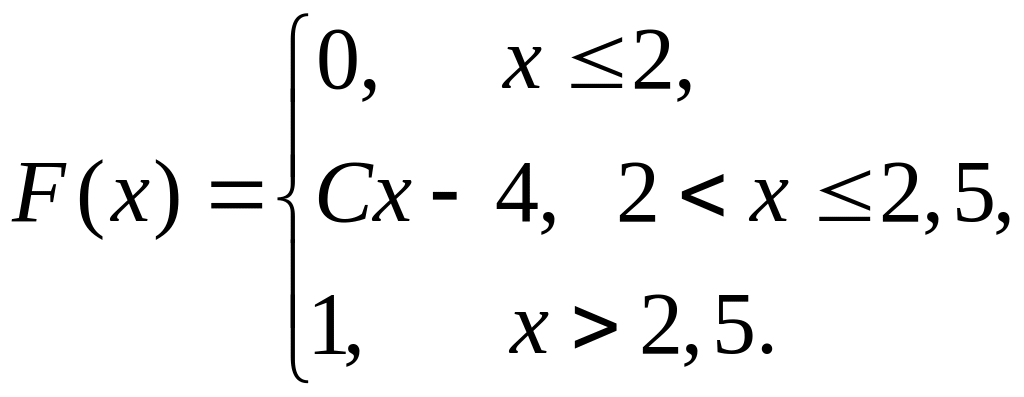
Тогда: 1) значение С равно…; 2) вероятность равна…

21. График плотности распределения вероятностей имеет следующий вид:

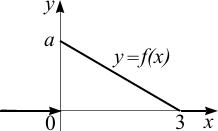
Тогда значение а равно…

22. График плотности распределения вероятностей непрерывной случайной величины X, распределённой равномерно в интервале , имеет вид:

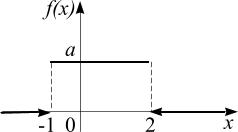
Тогда значение параметра а равно…

23. Случайная величина распределена равномерно на интервале (1; 5). Тогда ее математическое ожидание и дисперсия соответственно равны…

24. Непрерывная случайная величина X задана плотностью распределения вероятностей 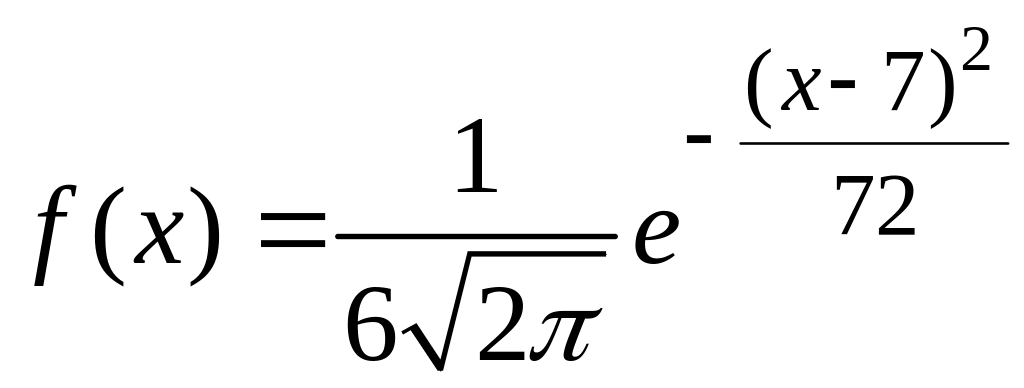. Тогда математическое ожидание и среднее квадратичное отклонение этой нормально распределенной случайной величины равны соответственно…

25. Пусть . Как изменится амплитуда нормальной кривой, если значение увеличить (уменьшить) в k раз?

26. Пусть . В каких четвертях координатной плоскости (первой, второй, третьей, четвертой) находится ось симметрии нормальной кривой, если ?

27. Из генеральной совокупности извлечена выборка объема :

	1	2	3	4
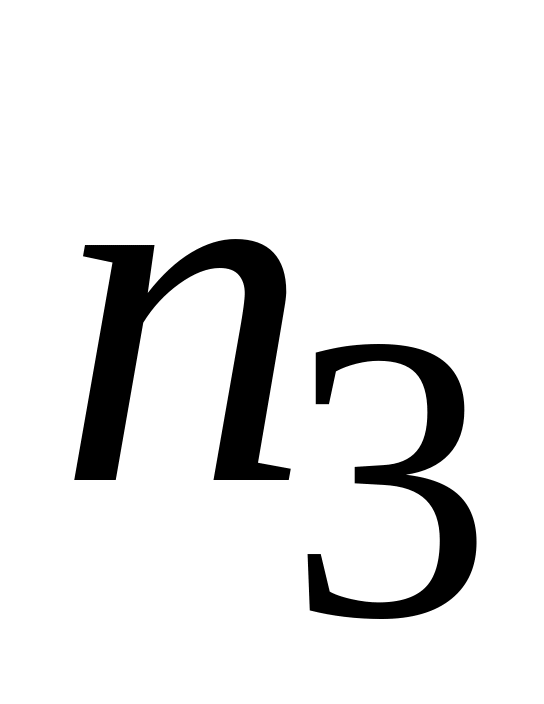
	12	4		19

Тогда =…

28. Статистическое распределение выборки имеет следующий вид:

	2	5	8	9
	3	4	6	4

Тогда относительная частота варианты равна…

29. Дана выборка объема n. Если каждый ее элемент увеличить в 5 раз, то выборочное среднее  (выберите правильное утверждение): 1) увеличится в 25 раз; 2) уменьшится в 5 раз; 3) не изменится; 4) увеличится в 5 раз.

30. Из генеральной совокупности извлечена выборка объема , полигон частот которой имеет вид

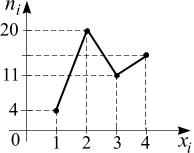
Тогда число вариант в выборке равно…

31. По выборке объема построена гистограмма частот:

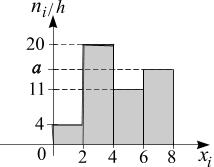
Тогда значение параметра а равно…

32. Мода вариационного ряда     равна…

33. Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): . Тогда несмещенная оценка математического ожидания равна…

34. Точечная оценка математического ожидания нормального распределения равна 10. Тогда его интервальная оценка может иметь вид (выберите правильное утверждение): 1) (8,5 ; 11,5);

2) (8,6 ; 9,6); 3) (8,4 ; 10).

35. Дана интервальная оценка (10,45; 11,55) математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна…

36. Если основная гипотеза имеет вид , то конкурирующей может быть (выберите правильные утверждения): 1) ; 2) ; 3) ; 4) .

37. Соотношением вида можно определить (выберите правильное утверждение): 1) двустороннюю критическую область; 2) левостороннюю критическую область; 3) область принятия гипотезы; 4) правостороннюю критическую область.

38. Выборочное уравнение парной регрессии имеет вид . Тогда выборочный коэффициент корреляции может быть равен (выберите правильное утверждение): 1) ; 2) ; 3) 0,6; 4) .

39. Выборочное уравнение парной регрессии имеет вид , причем выборочные с.к.о. . Тогда выборочный коэффициент корреляции равен…

40. При построении выборочного уравнения прямой регрессии вычислены выборочный коэффициент корреляции и выборочные с.к.о. . Тогда выборочный коэффициент регрессии Y на X равен…

О Г Л А В Л Е Н И Е

ЧАСТЬ I. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Введение …………………………………………………………….	3
Тема 1. Классификация событий. Различные определения вероятности……………………………………………………...	4
Индивидуальные задания к теме 1 ………………………	12
Тема 2. Теоремы сложения и умножения вероятностей ………..	19
Индивидуальные задания к теме 2 ………………………	23
Тема 3. Формула полной вероятности. Формула Бейеса………...	29
Индивидуальные задания к теме 3 ………………………	30
Тема 4. Схема Бернулли …………………………………………...	33
Индивидуальные задания к теме 4 ………………………	39
Тема 5. Случайные величины, их законы распределения и числовые характеристики ……………………………………	42
Индивидуальные задания к теме 5 ………………………	57
Тема 6. Равномерное и показательное распределения …………..	67
Индивидуальные задания к теме 6 ………………………	69
Тема 7. Нормальное распределение ………………………………	74
Индивидуальные задания к теме 7 ………………………	76
Тема 8. Примеры распределений, порожденных нормальным законом распределения ………………………………….	81
Индивидуальные задания к теме 8 ………………………	84
Тема 9. Системы двух дискретных случайных величин: таблица распределения, безусловные и условные законы распределения составляющих, линии регрессии, коэффициент корреляции………………………………….	88
Индивидуальные задания к теме 9 ………………………	93
ЧАСТЬ II. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Введение……………………………………………………………..	94
Тема 10. Описательные статистики ………………………………	95
Индивидуальные задания к лабораторной работе «Описательные статистики» ……………………………………	105
Тема 11. Проверка статистических гипотез ……………………...	117
Индивидуальные задания к лабораторной работе «Проверка статистических гипотез» …………………………..	124
Тема 12. Однофакторный дисперсионный анализ ……………….	126
Индивидуальные задания к лабораторной работе «Однофакторный дисперсионный анализ» ………………….	133
Тема 13. Корреляция и регрессия …………………………………	137
Индивидуальные задания к лабораторной работе «Корреляционный и регрессионный анализ» ………………...	149
ЧАСТЬ III. ПРИМЕРЫ ЛАБОРАТОРНЫХ РАБОТ ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ В СИСТЕМЕ MATHCAD..
Темы лабораторных работ и их основные цели…………………..	154
Лабораторная работа № 1. Распределения, связанные с нормальным законом распределения………………………..	158
Лабораторная работа № 2. Метод статистических испытаний (метод Монте-Карло)………………………………………	164
Лабораторная работа № 3. Описательные статистики…………...	167
Лабораторная работа № 4. Проверка гипотезы о нормальном распределении признака с помощью критерия Пирсона	174
Лабораторная работа № 5. Примеры проверки статистических гипотез……............................................................................	177
Лабораторная работа № 6. Однофакторный дисперсионный анализ	183
Лабораторная работа № 7. Корреляция и регрессия……………...	186
СПИСОК ЛИТЕРАТУРЫ ………………………………………	190
Приложение 1. Таблица значений функции Гаусса ……………..	191
Приложение 2. Таблица значений функции Лапласа …………...	193
Приложение 3. Критические точки распределения …………	195
Приложение 4. Критические точки распределения Стьюдента…	196
Приложение 5. Критические точки распределения Фишера…….	197
Приложение 6. Примеры тестовых вопросов по теории вероятностей и математической статистике……………	199

Учебное издание

Дементьев Сергей Николаевич

Слиденко Александр Михайлович

Стрыгина София Олеговна

ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

С ИСПОЛЬЗОВАНИЕМ

КОМПЬЮТЕРНОГО ПАКЕТА MATHCAD

Учебное пособие

Редактор С.А. Дубова

Корректор Н.В. Ульянова

Компьютерная верстка И.А. Остапенко

Подписано в печать 14.10.2010 . Формат 6084 ¹/₁₆.

Бумага офсетная. Печать офсетная. Гарнитура Таймс.

П.л. 12,9. Тираж 140 экз. Заказ №

Федеральное государственное образовательное учреждение

высшего профессионального образования

«Воронежский государственный аграрный университет имени К.Д. Глинки».

Типография ФГОУ ВПО Воронежский ГАУ