Основные понятия

В математической статистике важную роль играют некоторые законы распределения случайных величин, являющихся функ­циями независимых нормальных случайных величин. К ним отно­сятся распре­деления хи-квадрат, Стьюдента и Фишера.

Распределение хи-квадрат ( -распределение)

Пусть  независимые нормально распределенные стандартные случайные ве­ли­чины

Тогда распределение случай­ной величины

называется распределением хи-квадрат с степенями свободы .

Распределение Стьюдента ( распределение)

Пусть  независимые нормально распределенные стандартные случайные величины: Тогда случайная величина

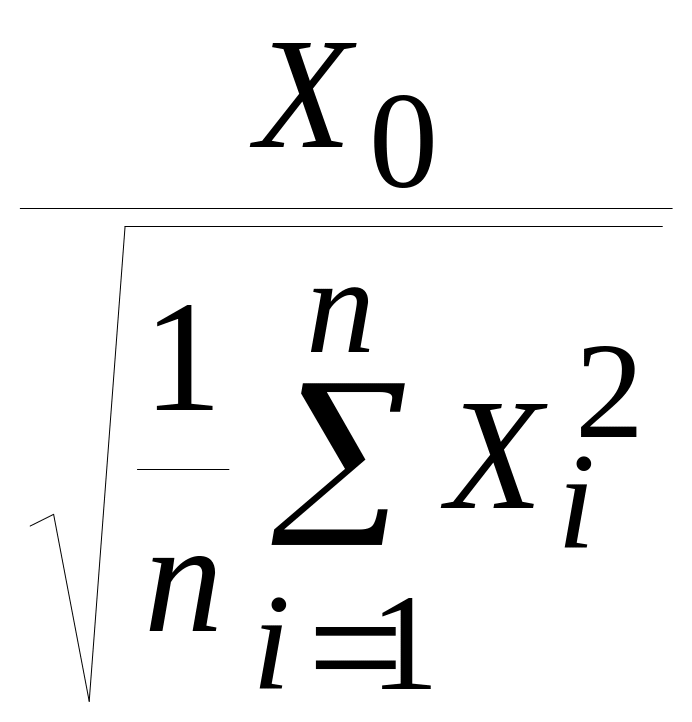
имеет по определению распределение Стью­дента (или распределение) с степенями свободы .

Распределение Фишера ( -распределение)

Пусть  независимые нормаль­ные случай­ные величины, причем

Тогда по определению случайная величина

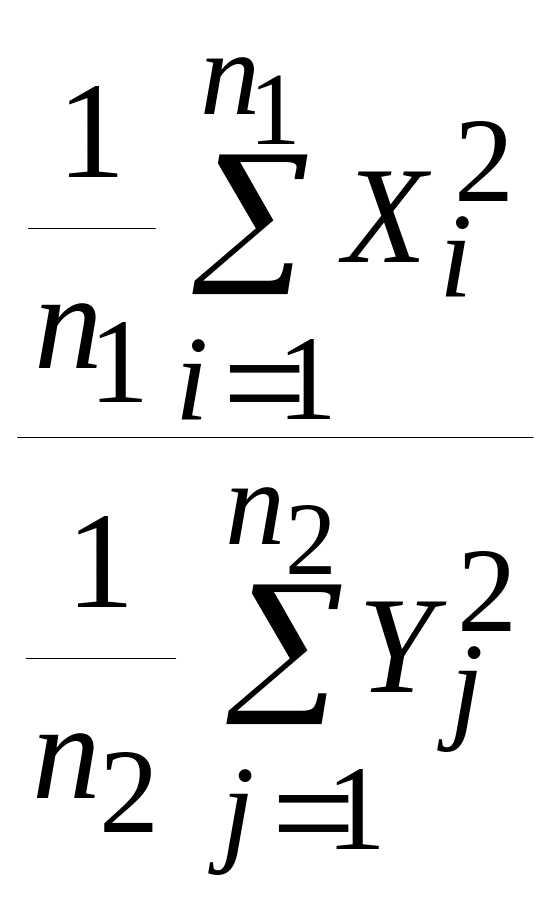
имеет распределение Фишера (или распределение) со степенями свободы .

На рис. 8.18.3 изображены графики плотностей вероятности рассматриваемых распределений.

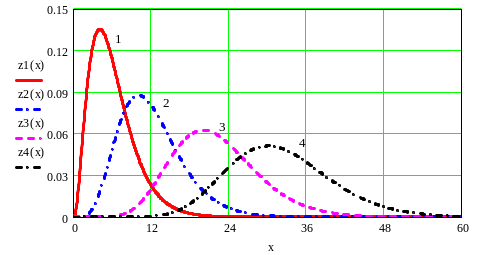Рис. 8.1. Кривая распределения при

n = 6 (1), n = 12 (2), n = 22 (3) и n = 32 (4)

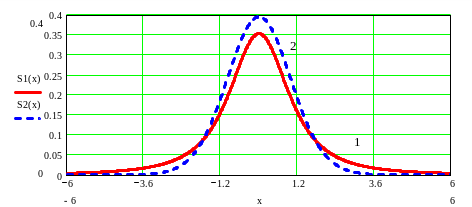
Рис. 8.2. Кривая распределения Стьюдента при

n = 1 (1) и n = 30 (2)

Рис. 8.3. Кривая распределения Фишера при

(1); (2); (3)

З а м е ч а н и я.

1.Можно показать, что каждое из рассмотренных выше распределений при неограниченном увеличении числа степеней свободы стремится к нормальному. Это достаточно хорошо прослеживается на рис. 7.17.3.

2.Критические точки рассматриваемых распределений можно найти в таблицах приложений 35.

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ К ТЕМЕ 8

Задача 8.1. Исходя из того, что

являются независимыми случайными величинами, привести примеры случайных величин

Вариант	k	m	p	q
130	Значения параметров назначьте сами

Примеры решения индивидуальных заданий

Пример 8.1. Заданы независимые случайные величины

Составить случайную величину, имеющую распределение .

Решение. Рассмотрим случайные величины 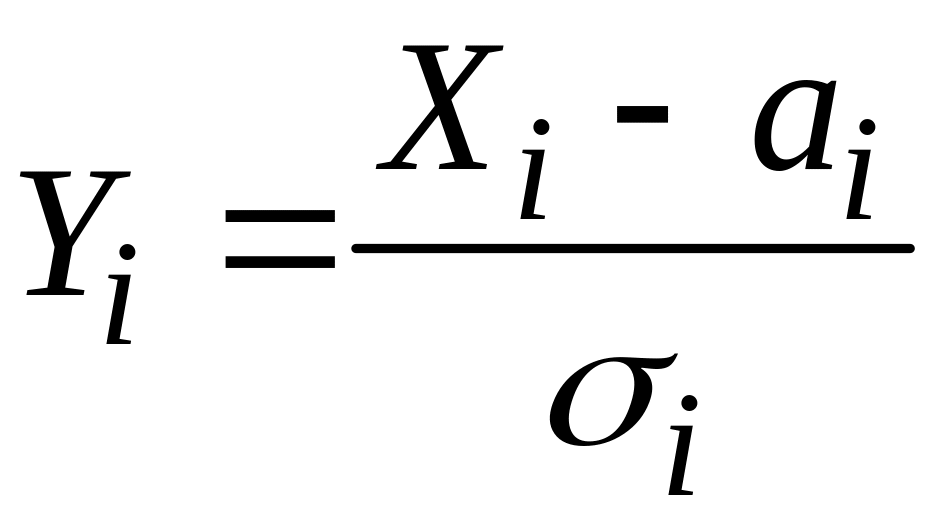, Они независимы, имеют нормаль­ные распределения. Найдем параметры этих распределений:

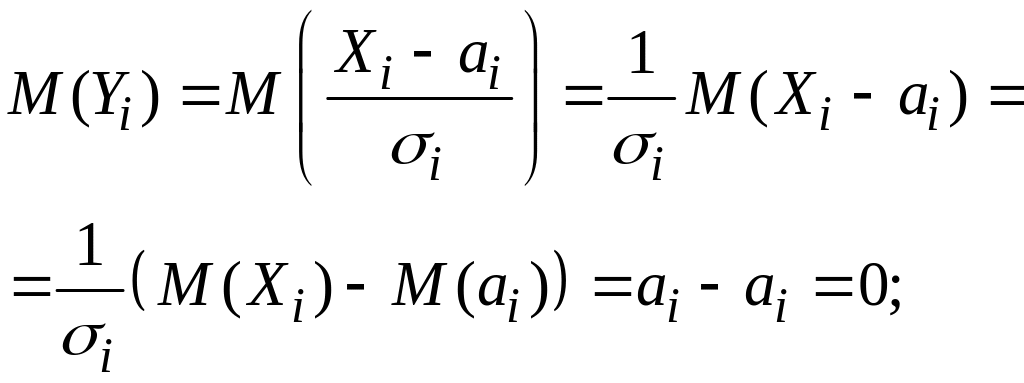
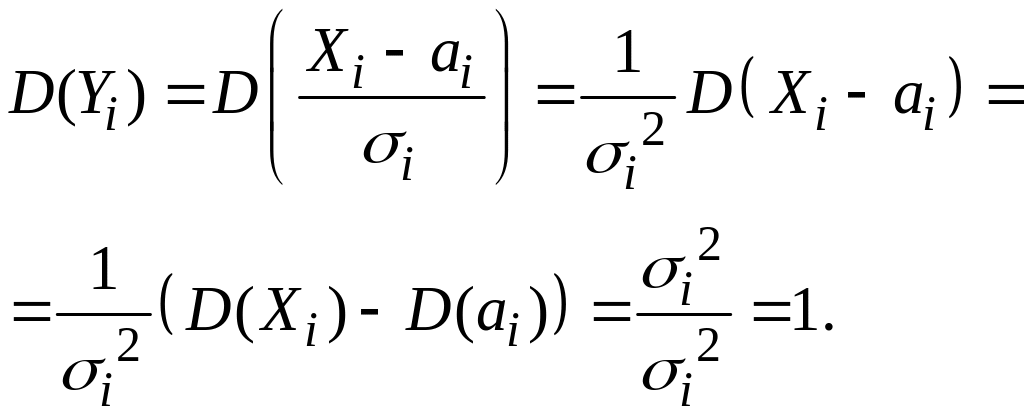
Отсюда и, следовательно,

,

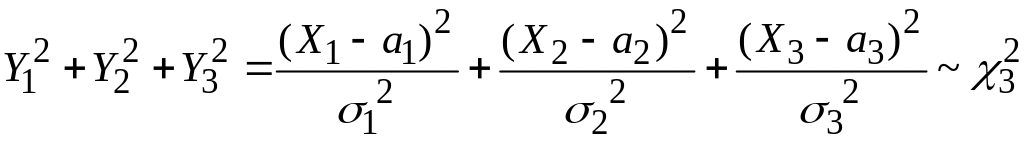т.е. имеет распределение хи-квадрат с тремя степенями свободы.

Пример 8.2. Заданы независимые случайные величины

Составить случайную величину, имеющую распределение Стьюдента с тремя степенями свободы ( ).

Решение. Случайные величины

имеют стандартные нормальные распределения ( ). Тогда, например, случайная величина

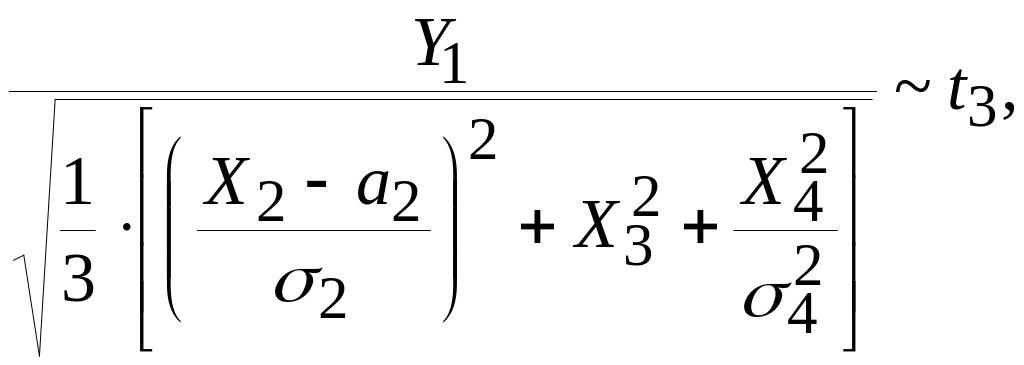
т.е. имеет рас­пределение Стьюдента с тремя степенями свободы.

Пример 8.3. Заданы независимые случайные величины ; ; ; ; .

Составить случайную величину, которая распределена по за­кону Фишера со степенями свободы

Решение. Рассмотрим случайные величины

Поскольку они имеют стандартные нормальные распределения, то случайная величина

,

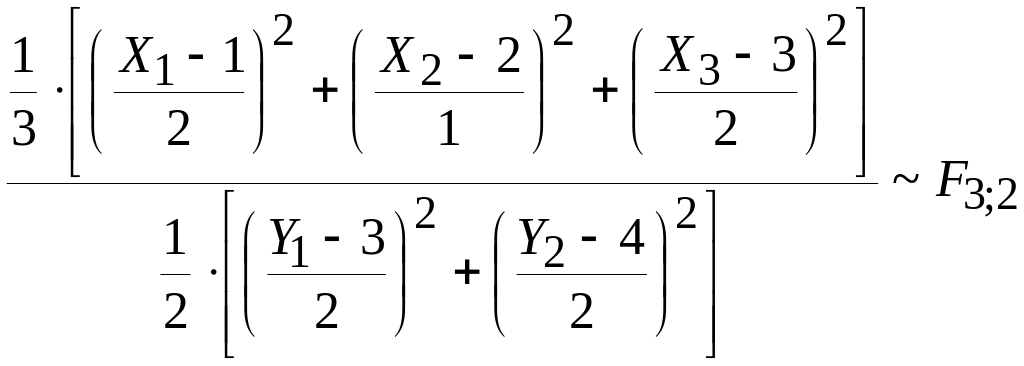т.е. имеет распределение Фишера со степенями свободы

КОНТРОЛЬНЫЕ ВОПРОСЫ К ТЕМЕ 8

1.Дайте определение закона распределения хи-квадрат.

2.Дайте определение распределения Стьюдента.

3.Распределение какой случайной величины называют распре­делением Фишера?

4.Как ведут себя законы распределений случайных величин , при

5.Как ведет себя закон распределения случайной величины при

6.Заданы независимые случайные величины Составить случайную величину, которая распределена по закону хи-квадрат с четырьмя степенями свободы.

7.Заданы независимые случайные величины Составить случайную величину, имеющую распределение Стьюдента с двумя степенями свободы.

8.Заданы независимые случайные величины Составить случайную величину, которая распределена по за­кону Фишера со степенями свободы

9.Случайная величина X имеет распределение хи-квад­рат с 4 степенями свободы. Используя таблицы критических точек распре­деления хи-квадрат, найти значения , если заданы вероят­ности со­бытий:

а) где ;

б) где

10.Пусть  независимые случайные вели­чины, причем Показать, что случайная величина имеет распределение

11.Случайная величина X имеет распределение Стьюдента с 10 степенями свободы. Используя таблицы критических точек распределения Стьюдента, найти значения если:

а) где

б) где

в) где

12.Случайная величина X имеет распределение Фишера со степенями свободы и Используя таблицы критических точек распределения Фишера, найти значения если заданы вероятности событий:

а) где

б) где

Тема 9.

СИСТЕМЫ ДВУХ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН: ТАБЛИЦА РАСПРЕДЕЛЕНИЯ, БЕЗУСЛОВНЫЕ И УСЛОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СОСТАВЛЯЮЩИХ, ЛИНИИ РЕГРЕССИИ, КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ