XVYggbpFw2

Это означает, что к содержимому строки C добавилось содержимое строки D. Таким образом один шаг алгоритма избавления от переходов без меток можно описать так:

Встолбце 1 выбираем любое состояние B. Допустим, оно находится

встроке A. К строке A поклеточно добавляем содержимое строки B (включая и элементы столбца fin).

Этот шаг проделывается до тех пор, пока добавляются новые элементы.

Внашем случае получим:

Убирая столбец 1 и строку D из-за того, что состояние D станет недостижимым, получим ответ:

Определение 12.3. Состояние автомата называется недостижимым, если нет ни одного пути из стартового состояния к данному состоянию. Состояние называется и непродуктивным если от данного состояния нет ни одного пути к какому-нибудь заключительному состоянию. Состояние называется бесполезным или лишним, если оно недостижимое или непродуктивное.

Автомат, в котором нет бесполезных состояний, называется при-

веденным.

Понятно, что здесь полная аналогия с соответствующими понятиями в КС-грамматиках. Как и в грамматиках можно избавиться от всех лишних

состояний автомата просто удаляя из графа как их вершины, так и все инцидентные им дуги. Повторив эту процедуру достаточное число раз мы получим автомат, эквивалентный исходному, и не содержащий лишних со-

стояний. Таким образом, любой автомат эквивалентен приведенному.

Упражнения

12.1. Построить автоматы, распознающие языки:

a)Множество всех цепочек вида an, где n – четное число.

b)Множество всех цепочек вида anbm.

c)Множество всех цепочек вида anbm, где n+m – четно.

d)Множество всех цепочек от букв a, b четной длины.

e)Множество всех цепочек от букв a, b нечетной длины.

f)Множество всех цепочек от букв a, b, в которых число букв a четно, а число букв b нечетно.

g)Множество всех цепочек от букв a, b, в которых число букв a четно и число букв b четно.

h)Множество всех цепочек от букв a, b, в которых число букв a нечетно и число букв b нечетно.

i)Множество всех цепочек от букв a,b,c которые не начинаются на букву c, не заканчиваются на c и в которых нет двух рядом стоящих c.

j) Множество всех цепочек от букв a, b вида т1 т2… тk , где т = abma.

12.3.Построить регулярную грамматику, определяющую язык, распознаваемый данным автоматом:

a)

b)

c)

d)

12.4.Автоматы упражнения 12.3 записать в табличном виде.

12.5.Данный автомат переделать в эквивалентный автомат, в котором нет переходов (дуг) без меток:

a)

b)

c)

12.6.Данный автомат, определяемый таблицей, переделать в эквивалентный приведенный автомат, в котором нет переходов

(дуг) без меток:

a)

13. ДЕТЕРМИНИРОВАННЫЕ АВТОМАТЫ

Определение 13.1. Конечный автомат A =<Q,T, ,S,F> называется

детерминированным, если для любых q Q, t T множество состояний 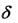(q,t) состоит не более, чем из одного элемента. Назовем автомат недетерминированным, если он не является детерминированным.

Детерминированность автомата на языке графов означает, понятно, что из одной и той же вершины не может выходить более одной дуги, помеченной одним и тем же терминальным символом. Если в автомате допускаются дуги без меток, и такая дуга выходит из какой-то вершины вместе с еще какой-нибудь дугой, то такой автомат также считаем недетерминированным. Таким образом детерминированность означает, что из любого положения у автомата может быть не более одного варианта сделать следующий шаг. Имея на входе какую-нибудь цепочку терминалов такой автомат, может проделать “однозначное” вычисление для того, чтобы узнать, воспринимается или нет. Другими словами автомат работает автоматически, как и полагается автомату. Нигде не надо гадать, по какому из нескольких возможных переходов следует идти, как это обычно бывает при работе недетерминированного автомата.

Мы знаем, что любой регулярный язык определяется конечным автоматом. Алгоритм построения по регулярной грамматике такого автомата

вобщем случае дает недетерминированный автомат. Например, наличие в грамматике продукций вида A аB|aC влечет наличие переходов из состояния A в состояния B и C, помеченные одной и той же буквой a. Но оказывается, что любой недетерминированный автомат можно переделать

вэквивалентный детерминированный.

Теорема 13.1. Любой недетерминированный автомат эквивалентен некоторому детерминированному автомату.

Доказательство. Доказательство теоремы, как и раньше, даст нам алгоритм переделки недетерминированных автоматов в детерминированные. Идея весьма проста. В случаях, когда из одного состояния A исходит целый веер ребер, помеченных одной и той же буквой a, надо вместо всех состояний, на которые указывает a, ввести одно. Иными словами - некоторые множества состояний сжать в точку.

Итак, пусть A =<Q,T, ,S,F> произвольный (недетерминированный) автомат. Считаем, что в нем нет переходов без меток (от них надо избавиться в первую очередь). Строим по нему детерминированный Adet = <

Qdet,T,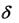det,Sdet,Fdet> (терминалы T остаются прежними). Все состоя-

ния автомата Adet – будут некоторыми множествами состояний автомата

A.

Полагаем стартовым состоянием Sdet = {S} – множество из одного

элемента.

Определение Sdet - это первый шаг построения. Дальше делается серия однотипных шагов до тех пор, пока у Adet продолжают появляться

новые состояния.

Общий шаг. Состоит из двух этапов.

1. Берем любое из построенных состояний P нового автомата и любой терминал a. Рассмотрим множество

R = {B Q | A P , что из A в B выходит дуга, помеченная буквой a} Если R не является элементом множества Qdet уже построенных состоя-

ний автомата Adet, то добавляем его к Qdet.

2. Из P в R проводим дугу с меткой a (если ее еще не было), т.е. полагаем

det (P , a) = {R}.

Процесс выполнения шагов завершается, когда новых состояний или переходов не возникает. После этого остается определить заключительные

На каком-то шаге рассматриваются R1 и b, по которым конструируется (или находится) R2, в котором лежит B и в которое из R1 есть переход, помеченный буквой b. Аналогично находятся R3, R4, причем R4 является

заключительным, т.к. содержит символ D. Теперь очевидно, что автомат Adet воспринимает цепочку abcd. Ясно также, что подобное рассуждение

справедливо для любой цепочки (независимо от того, повторяются в ней какие-то буквы или нет) и для любых сопутствующих ей состояний автомата A .

Пусть L(Adet). Как и выше, для примера пусть = abcd. Имеем последовательность конфигураций автомата Adet:

< Sdet , abcd > < R1 , bcd > < R2 , cd > < R3 , d > < R4 , >

для некоторых состояний R1, R2, R3, R4, причем R4 является заключительным состоянием автомата Adet. Значит Adet имеет переходы:

, , , .

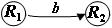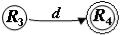Рассмотрим эту цепочку от конца к началу – в обратном направлении. Во-первых, видим, что в R4 имеется какое-то заключительное состоя-

ние автомата Adet. Пусть это D. Согласно основному шагу построения Adet множество R4 – это совокупность всех концов дуг автомата A, выхо-

Детерминированный автомат A = <Q,T, ,S,F> называется полным,

если множество (q,t) всегда состоит ровно из одного элемента. Это означает, что для каждого терминала a из каждого состояния выходит точно одно ребро, помеченное символом a. Для полных детерминированных автоматов можно (q,t) считать не множеством, а непосредственно тем элементом, из которого оно состоит.

Замечание 13.1. Легко видеть, что любой детерминированный неполный автомат A эквивалентен полному детерминированному конечному автомату. Для построения такого автомата A Err применим простую конструкцию. Присоединяем к A дополнительное состояние Err и полага-

ем (q,t)=Err для всех случаев неопределенного (q,t). Естественно, (Err,t) = Err. Состояние Err не является заключительным. Его можно интерпретировать как своеобразный обработчик ошибок.

Заметим еще, что если автомат является приведенным и не полным, то A Err приведенным уже не будет. В нем будет содержаться единственное

бесполезное состояние Err. Оно, очевидно, является непродуктивным.

Пример 13.1. Рассмотрим автомат на Рис. 1

Рисунок 1

Соответствующий детерминированный автомат вычисляем в виде таблицы:

В первом столбце таблицы перечисляются состояния нового автомата: S,G,H,I,C,J,K,… . В столбиках, помеченных терминалами, как и полагается в таблице, записаны значения функции переходов. В столбце справа перечисляются состояния старого автомата, из которых состоят новые. Напомним, что новые состояния являются множествами старых.

Построение таблицы начинается с первой строки. Записываем в нее S – стартовое состояние нового автомата. Оно, как множество, состоит из единственного элемента – стартового состояния S старого автомата. В правой колонке пишем это S, указывая этим, из каких элементов состоит S. Теперь вычисляем, какие множества порождаются этим S под действием каждого из терминалов a,b,c. Сначала для a. Глядя на схему старого автомата, видим, что из S выходят три дуги с меткой a в вершины A,E,D. Они и

составляют множество G. Буква G выбрана потому, что это первая буква, не использовавшаяся раньше. Теперь должно быть понятно, откуда во второй строке взялось G и A,E,D в последнем столбце. Клетки в столбцах под терминалами пока оставляем в покое. Продолжаем вычислять первую строку.

Теперь очередь – определить, во что превращается S под действием b. Но из S не выходит ни одной дуги с меткой b. Соответственно и из S таких дуг выходить не будет. Аналогично из S не будет выходить дуг с меткой c. Поэтому в строке 1 под терминалом a стоит G, а под b,c не стоит ничего. Это заканчивает заполнение строки 1.

Но появилась строка 2 с состоянием G и с его содержимым A,E,D.

Она требует вычисления Ga, Gb, Gc. Имеем Ga= , Gb={A,B}, Gc={ A,E,F}. Обозначая H={A,B}, I={A,E,F}, заполняем до конца строку 2. Затем добавляем две новые строки 3 и 4 для H и для I.

Вычисляем строку 3. Имеем, что Ha={C}, Hb= , Hc={A,F}. В результате получаем еще пару состояний C={C}, J={A,F}, которые займут строки 5 и 6. Мы обозначили состояние, содержащее единственный элемент C тоже буквой C. Только ради удобства и без всякого намека на глубокий смысл.

Вычисляем строку 4. Имеем, что Ia={S,E}, Ib={A,B}, Ic={A,F}. Множество {S,E} еще не встречалось. Обозначаем K={S,E}. Далее находим, что {A,B}= H и {A,F} = J. В результате заполняется строка 4. Мы пришли к ситуации, изображенной в последней таблице. Далее процесс продолжается до тех пор, пока процесс заполнения строк в терминальных столбцах не “догонит” процесс появления новых состояний. Т.к. всевозможных подмножеств множества {S,A,B,C,D,E,F} конечен, то рано или поздно это произойдет. В данном примере получится таблица:

Граф для этого автомата изображен на Рис 2.

Рисунок 2

Для того, чтобы почувствовать разницу между недетерминированным и детерминированным автоматом попробуйте распознать цепочку abca сначала автоматом на Рис.1, а затем – автоматом на Рис. 2.

Упражнения

13.1.Для данных автоматов построить им эквивалентные детерминированные:

a)