iSswV45XbM

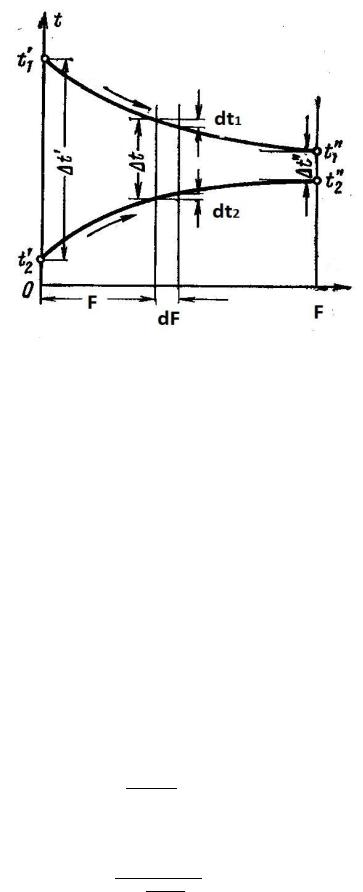
Рисунок 9. Изменение температурного напора между теплоносителями по длине поверхности теплообмена

Аналитическое решение уравнения теплопередачи позволяет сделать вывод, что вдоль поверхности теплообмена температурный напор изменяется по экспоненциальному закону

Следовательно, в теплообменниках с противоточной схемой движения t

уменьшается в случае, когда W1 < W2 , т.е. m > 0, а при W1 > W2 , т.е. когда m < 0, температурный напор t увеличивается (см. Рис. 9). Выполняя

усреднение температурного напора по всей поверхности теплообмена получают расчетную формулу среднелогарифмического температурного напора:

= ; (3.15)

или же выражение (1.15) записывают в таком виде

= , (3.16)

20

где – большая разность температур между теплоносителями;

– меньшая разность температур между теплоносителями.

Средняя разность температур, представленная формулами (3.15) и (3.16), может быть использована как при прямотоке, так и при противотоке при условии постоянства массового расхода теплоносителей и коэффициента теплопередачи вдоль всей поверхности теплообмена. В случае незначительного изменения температуры теплоносителей вдоль

Для сложных схем движения теплоносителей определение температурного напора по формулам (3.15 - 3.17) будет не точным, поэтому для учета особенностей теплообмена в этом случае используют экспериментально полученные зависимости между величинами P и R для

собой отношение водяных эквивалентов теплоносителей или изменений температур теплоносителей. Стоит отметить, что тепловая эффективность рассматривается, как отношение изменения температуры холодного теплоносителя к максимально возможной разности температур, т. е. к разности между входными температурами обоих теплоносителей:

Величина P всегда меньше единицы, а R может быть и меньше, и больше единицы в зависимости от соотношения водяных эквивалентов W1 и W2 . На рисунках Приложений 27 – 32 даны такие зависимости для перекрестного, одновременно прямоточного и противоточного, и многократно перекрестного схем движения.

Для расчета коэффициента теплопередачи через цилиндрическую поверхность трубки необходимо помнить, что в общем случае передача тепла через цилиндрическую стенку конкретных размеров определяется выражением

21

где l -длина трубки;

λ – теплопроводность материала трубки;

dвн и dнар – внутренний и наружный диаметры трубки;

α1 и α2 – соответственно коэффициенты теплоотдачи внутри и снаружи трубки;

t1 и t2 – соответственно температуры горячего и холодного теплоносителей.

Относя этот тепловой поток к поверхности, которая соответствует среднему диаметру трубки, получают выражение для плотности теплового потока через поверхность среднего диаметра, а учитывая связь между плотностью теплового потока, поверхностью теплообмена и коэффициентом теплопередачи k получают следующую расчетную формулу:

k = . (3.21)

В практических расчетах по формуле (3.21) руководствуются следующим правилом:

при α1 > α2 за средний диаметр принимают наружный диаметр;

при α1 < α2 за средний диаметр принимают внутренний диаметр;

при α1 ≈ α2 за средний диаметр принимают dср = (dвн + dнар).

Имеющаяся практика расчета тонкостенных труб, в которых dнар/dвн <2, а определение коэффициента теплопередачи ведется по формуле справедливой для плоской стенки

приводит к дополнительной ошибке порядка 4% и поэтому при современном уровне использования вычислительной техники не является оправданной.

Очевидно, что для определения коэффициента теплопередачи необходимо рассчитать коэффициенты теплоотдачи с обеих сторон поверхности теплообмена. Для этого могут быть использованы эмпирические критериальные уравнения, полученные на основе

22

экспериментальных исследований различных видов теплообмена, характера и режима течения теплоносителя, расположения поверхности теплообмена. Коэффициенты теплоотдачи, рассчитанные по таким уравнениям, относят к рассчитанным для идеальных гладких труб или пучков труб, поскольку вводят такие допущения, как стационарный режим работы теплообменника, участие в теплообмене в одинаковой степени любой части потока теплоносителя, постоянство теплоемкости теплоносителя, отсутствие потерь теплоты в окружающую среду.

Использование критериальных уравнений предполагает следующий стандартный алгоритм расчета коэффициентов теплоотдачи:

1.В зависимости от вида конвективного теплообмена выбирают конкретное уравнение из справочной литературы.

2.Находят для выбранного уравнения значения определяющих параметров – характерный геометрический размер, температуру и теплофизические свойства теплоносителя при этой температуре, скорость потока (исходя из заданного расхода теплоносителя).

3.Определяют режим течения теплоносителя по критерию Рейнольдса Re для вынужденного движения или Релея Ra при свободном движении и уточняют вид критериального уравнения.

4.Рассчитывают по критериальному уравнению число Нуссельта Nu, являющееся безразмерным коэффициентом теплоотдачи.

5.Вычисляют коэффициент теплоотдачи, используя

функциональную связь α = Nu.

Однако, решение критериальных уравнений по указанному алгоритму предполагает знание температур поверхности теплообмена. Поскольку они неизвестны, то в первом приближении их задают, руководствуясь следующим общепринятым правилом:

- со стороны горячего теплоносителя температура стенки определяется, как разность между температурой горячего теплоносителя и ½ сренелогарифмического температурного напора

:

-со стороны холодного теплоносителя, учитывая высокую теплопроводность материала стенки, выбирают температуру стенки на 1-3 градуса меньше, чем со стороны горячего теплоносителя:

23

Теплопроводность материала стенки определяют из справочных данных при средней температуре стенки, равной ½(t1ст+t2ст). Дальнейшее уточнение t1ст и t2ст производят, используя метод последовательного приближения. Для этого по критериальным уравнениям рассчитывают коэффициенты теплоотдачи α1 и α2. Затем вычисляют коэффициент теплопередачи по формуле (3.21) или (3.22) и определяют плотность теплового потока q через поверхность теплообмена:

Зная плотность теплового потока, определяют температуры стенки на горячей и холодной стороне:

t1ст = t1 - , (3.26)

Процентное расхождение между полученными значениями и заданными в первом приближении оценивают допускаемой величиной, обычно в 1 – 5 %. Если расхождение больше установленной нормы, то расчет повторяют, задаваясь уже полученными из расчетов значениями t1ст и t2ст.

Возможен и другой способ определения температур t1ст и t2ст. Для этого задаются в первом приближении ожидаемыми значениями коэффициентов теплоотдачи α1 и α2, выбирая из справочной литературы диапазоны, реально существующие для случаев нагрева и охлаждения жидкостей, газов или кипения и пленочной конденсации жидкостей. В этом случае теплопроводность материала стенки находят из справочников при температуре, равной среднему значению температур горячего и холодного теплоносителей ½(t1+t2). Учитывая, что разность температур между теплоносителями складывается из суммы разностей температур между горячим теплоносителем и стенкой, разности температур между горячей и холодной стороной стенки и разности между температурой стенки с холодной стороны и холодным теплоносителем, можно составить два уравнения, которые определяют связь между этими температурными

24

стороны;

=– термическое сопротивление теплопроводности стенки;

=– термическое сопротивление конвекции с холодной

стороны;

–толщина стенки трубы.

Решая совместно эти два уравнения, находят выражения для температур стенки с горячей стороны t1ст и с холодной t2ст:

критериальным уравнениям, и, если расхождение между полученными значениями коэффициентов и заданными превышают установленную точность, расчет повторяют, задаваясь последними полученными расчетным способом величинами и .

При движении теплоносителя без изменения фазового состояния в прямых гладких круглых трубах, в щелевых каналах пластинчатого теплообменника или в каналах некруглого сечения могут быть использованы следующие критериальные уравнения:

1) при ламинарном вязкостном движении, когда произведение критериев Грасгофа Gr и Прандтля Pr меньше 8·105, среднее значение критерия Нуссельта Nuср определится уравнением [2, С. 212],

в котором l – длина трубки, – поправка на гидродинамический начальный участок, d - определяющий размер, которым может быть либо внутренний диаметр трубы , либо эквивалентный диаметр канала сложной формы dэкв:

25

либо (для внешнего прохода теплоносителя в межтрубном пространстве кожухотрубного теплообменника)

dэкв = , (3.35)

где – число трубок;

физические свойства жидкости, входящие в критерии уравнения,

коэффициент εl, учитывающий поправку на гидродинамический начальный участок, выбирают из следующей Табл. 1 [2, С. 213].

Таблица 1

Значения εl при ламинарном режиме

2) при ламинарном вязкостно-гравитационном режиме движения, когда произведение критериев Грасгофа и Прандтля Gr· Pr>8·105 [6, С. 374]

здесь за определяющую температуру принимают среднюю температуру жидкости в трубе.

За определяющую температуру в этом уравнении принимают среднюю температуру соответствующего теплоносителя на входе и выходе из

26

теплообменника tср = ( + ), а за определяющий размер – эквивалентный

диаметр dэкв равный учетверенной площади канала, деленной его полный периметр (для круглых труб dэкв равен геометрическому диаметру трубы).

4) при переходном режиме движения, когда 2300 <Re <104 [6, С. 378]

При расчете теплообмена в изогнутых трубах в вышеприведенных уравнениях полученное число Nuср умножают на поправочный коэффициент εl , который определяется выражением [2, С. 219]

где – радиус изгиба трубы.

5) при движении теплоносителя в пучке труб под углом атаки ψ = 90о

предложены следующие зависимости для расчета среднего значения числа

Nu [1,5, С. 104]:

6) при пленочной конденсации водяного пара и ламинарном стекании пленки под действием силы тяжести, которое происходит, если dнар < 20·( )0,5, используется формула для расчета среднего значения

коэффициента теплоотдачи, предложенная Нуссельтом [2, С. 272]:

27

где a = 0,943, b = h – т.е. высоте вертикальной стенки или тубы, a = 0,728, b = dнар – для горизонтальной трубы,

–поверхностное натяжение пленки,

–плотность пленки,

–ускорение свободного падения,

–температура насыщения водяного пара.

6)теплоотдача при развитом пузырьковом кипении воды в условиях свободного движения преимущественно зависит от тепловой нагрузки q и

давления насыщения pн, поэтому в практических расчетах ограничиваются применением эмпирических формул, справедливых в диапазоне давлений от 0,1 до 4 Мпа, и полученных при анализе и обработке экспериментальных данных [2, С. 311]:

где t соответствует разности температур стенки tст и насыщения водяного пара .

7) теплоотдача при пузырьковом кипении и вынужденной конвекции в трубах должна учитывать гидродинамическое влияние; такое влияние учитывается на практике отношением коэффициента теплоотдачи по формулам развитого кипения, когда отсутствует воздействие скорости потока на теплообмен, т. е. по формулам (3.45, 3.46), и коэффициента теплоотдачи по формулам вынужденного конвективного теплообмена однофазной жидкости, например, по формуле (3.37). Интерполяционная зависимость при этом имеет вид [2, С. 317]:

= . (3.47)

Если это отношение меньше 0,5, то среднее значение коэффициента теплоотдачи αср рассчитывают по формулам (3.45, 3.46), при величине отношения больше 2 среднее значение αср рассчитывают по формуле (3.37), а в случае, когда отношение лежит в диапазоне 0,5 – 2 коэффициент теплоотдачи αср определяют по формуле:

28

8) теплоотдача при использовании в качестве теплоносителя излучающего газа представляет собой сложный теплообмен и должна учитывать суммарный коэффициент теплоотдачи, что предполагает метод раздельного учета теплообмена конвекцией и излучением; в этом случае суммарное значение среднего коэффициента теплоотдачи будет включать конвективную составляющую αк и лучистую αл :

Коэффициент αл определяют после расчета плотности лучистого теплового потока qл, который согласно закону Стефана-Больцмана может быть определен по приближенной формуле [5, С. 176]:

где – коэффициент излучения абсолютно черного тела = 5,67 Вт/(м2·K4),

–степень черноты газа,

–степень черноты поверхности теплообмена,

–среднее значение абсолютной температуры газа, К,

–среднее значение абсолютной температуры стенки, К.

Вид уравнения (3.50) предполагает передачу тепла от объема газа к более холодной стенке, поэтому степень черноты нужно выбирать при температуре . Если же поток тепла направлен от стенки к газу, то величину нужно выбирать при температуре . Это позволяет учесть то обстоятельство, что поглощательная способность газа по отношению к излучению от стенки не равна его степени черноты.

В практических технических расчетах наибольший интерес представляет степень черноты газового объема. Для углекислого газа и водяного пара выполнены многочисленные исследования и их результаты для удобства пользования сведены в номограммы (в частности, номограмма для СО2 представлена в Приложении 24). В ней степень черноты СО2 приведена в зависимости от произведения парциального давления газа p и длины пути луча l. Номограмма построена с учетом того, что излучение проходит через единичную площадку из окружающей её газовой полусферы с

29