Шифр Вернама

Этот шифр был предложен в 1926 году американским инженером Гилбертом Вернамом и использовался на практике, но доказательство его невскрываемости было получено значительно позже Шенноном[2]. Для этого шифра также часто используется название «одноразовый блокнот». Рассмотрим этот шифр для двоичного алфавита, так как очевидно, что в случае практической реализации на компьютере, данный шифр легко может быть сведён к данному случаю. Как известно, любая информация на компьютере физически хранится и обрабатывается именно в двоичном коде.

Пусть исходное сообщение состоит из символов, т.е. существует всего различных сообщений . В шифре Вернама предполагается, что ключ также состоит из символов (количество различных ключей будет ) и все ключи используются с равной вероятностью. Это означает, что вероятность появления любого ключа будет равна . Более того, это определение является весьма близким к определению случайной последовательности, так как все символы равновероятны и независимы.

Пусть необходимо зашифровать некоторое сообщение при помощи выбранного ключа . Тогда зашифрованное сообщение получается по формуле:

где - сложение по модулю 2. Другими словами, шифрование происходит за счет посимвольного сложения по модулю 2 сообщения и ключа. Так как сложение по модулю 2 является взаимообратной операцией, то есть , то получаем, что для дешифрования сообщения необходимо применить следующую формулу:

Докажем, что полученное в результате шифрования сообщение, так же как и ключ, будет являться случайной последовательностью. Для начала необходимо рассмотреть таблицу истинности для функции сложения по модулю 2 (побитовое исключающее или).

x	y
0	0	0
0	1	1
1	0	1
1	1	0

Пусть вероятности сообщения известны и равны , при этом символы ключа равновероятны, т.е. . Тогда определим вероятности зашифрованного сообщения:

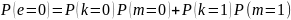
Подставим в формулы значения вероятностей сообщений и ключа и получим:

Таким образом мы доказали, что все символы зашифрованного сообщения будут равновероятны, как и символы ключа, что характеризует зашифрованную последовательность как случайную.

При выполнении работы допускается использовать любые алгоритмические генераторы псевдослучайных чисел, в том числе из стандартных библиотек, тем не менее, следует учитывать равномерность распределения символов в ключе. Т.е. при генерации случайного байта информации необходимо, чтобы его значение находилось в интервале [0,255].

Электронная подпись Криптографическая хэш-функция

Во многих криптографических алгоритмах используются хэш-функции, обладающие определёнными свойствами, опишем подобные функции:

Криптографическая хэш-функция – это одностороннее отображение бесконечного множества объектов 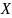на конечное фиксированное множество натуральных чисел 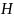, обладающее следующими свойствами:

1. Вычисление функции является относительно простой операцией и должно выполняться достаточно быстро.

2. Обратное вычисление наоборот является крайне трудоёмкой задачей, невыполнимой для современного уровня развития вычислительной техники.

3. Нахождение двух разных объектов , для которых значение функции будет идентичным является также крайне трудоёмкой задачей, невыполнимой при текущем уровне развития вычислительной техники.

4. Трудоёмкой (невыполнимой) задачей также является нахождение любого объекта , для которого выполняется равенство при известном значении .

Семейство международных стандартов на такие функции называется SHA (secure hash algorithm), в России существуют аналоги в виде ГОСТов. На данный момент самой надёжной функцией считается SHA3, основанная на алгоритме Keccak[3].

При выполнении лабораторных работ следует пользоваться алгоритмами с уровнем безопасности не ниже чем у алгоритма MD5. Рассмотрим подробнее именно этот алгоритм, ставший в своё время основой для первого семейства криптографических функций SHA1. Подробное описание алгоритма можно найти в [4]. Естественно при этом допускается реализовывать функцию самому, а применить любую из уже разработанных библиотек (например, openssl[5]).

Ниже приведем пример использования библиотеки openssl:

#include <stdio.h>

#include <string.h>

#include <openssl/sha.h>

 

int main() {

    unsigned char digest[SHA256_DIGEST_LENGTH];

    const char* string = "hello world";

 

    SHA256_CTX ctx;

    SHA256_Init(&ctx);

    SHA256_Update(&ctx, string, strlen(string));

    SHA256_Final(digest, &ctx);

 

    char mdString[SHA256_DIGEST_LENGTH*2+1];

    for (int i = 0; i < SHA256_DIGEST_LENGTH; i++)

        sprintf(&mdString[i*2], "%02x", (unsigned int)digest[i]);

 

    printf("SHA256 digest: %s\n", mdString);

 

 

    return 0;

}

Здесь SHA256_Update используется для обновления значения хэша. Эту функцию можно использовать, например, при хэшировании файла, если выполнять чтение побайтово (или по блокам) и обновлять для каждого байта (блока) значение хэша.

Электронная подпись

Прежде чем рассматривать конкретные алгоритмы, сформулируем основные свойства, которыми должна обладать любая подпись (как электронная, так и рукописная):

1. Подписать документ от своего имени может только один человек, т.е. невозможно подделать подпись другого человека.

2. Автор подписи не может от неё отказаться, в случае споров должно быть возможно привлечение третьих сторон (например, суда) для подтверждения подлинности подписи.

3. Подпись должна защищать целостность документа и подтверждать, что подписавший его человек ознакомлен с содержимым.

На самом деле, реализовать эти свойства в электронной подписи во многом проще и удобнее, чем в физическом исполнении. Рассмотрим подробнее, как это может быть реализовано, на примере следующего алгоритма.

Уточнение по реализации лабораторных работ по теме «электронная подпись»:

В рамках лабораторной работы необходимо использовать криптографическую хэш-функцию с уровнем безопасности не ниже md5. Все подобные функции формируют в качестве хэш-функции файла большое число размером 16/32/64 байт. Рассматриваемые ниже алгоритмы подписи предполагают работу с результатом хэш-функции как с одним числом, и это условие действительно будет выполнено, если во всех алгоритмах использовать «длинную арифметику» и работать с числами порядка 1024 бита. Тем не менее, так как требования к лабораторным работам позволяют использовать стандартные типы данных, предлагается следующий подход. Представить значение хэш-фукнции как массив байт, и каждый из этих байт подписать отдельно, применив к нему алгоритм подписи с одними и теми же изначальными параметрами (общие данные, секретный и открытый ключи).