
- •10.05.02 Информационная безопасность телекоммуникационных систем, специализация Защита информации в системах связи и управления (очная форма обучения)
- •1. Цель работы
- •2. Программа лабораторной работы
- •4. Расчетные формулы
- •6.5 Измерение частоты и периода гармонических сигналов резонансным частотомером.
Федеральное агентство связи
федеральное государственное бюджетное образовательное учреждение
высшего образования
«Сибирский государственный университет телекоммуникаций и
информатики»
Кафедра передачи дискретных сообщений и метрологии
10.05.02 Информационная безопасность телекоммуникационных систем, специализация Защита информации в системах связи и управления (очная форма обучения)
Лабораторная работа 3.6
Выполнил:
студент ФАЭС,
гр. АБ-75 /А.Е.Карелин/
«__»_________ 2021 г. (подпись)
Проверил:
Доцент каф. ПДС и М /И.Н. Запасный/
«__»_________ 2021 г. (подпись)
Новосибирск 2021.
1. Цель работы
1.1 Освоить методы измерения частоты и периода электрических сигналов специализированными средствами измерений.
1.2 Приобрести практические навыки работы с цифровыми и резонансными частотомерами, измерительными генераторами.
1.3 Получить практические навыки обработки результатов измерения частоты и периода сигналов, оценки погрешности (неопределенности) результатов измерений и их оформление.
2. Программа лабораторной работы
2.1 Измерение частоты и периода источника гармонических колебаний с помощью цифрового частотомера.
2.2 Измерение периода и частоты гармонических колебаний с помощью цифрового периодомера.
2.3 Измерение частоты и периода гармонических сигналов резонансным частотомером.
3. Описания средств измерения лабораторного стенда.
Электронный цифровой частотомер. [1, стр.17]
Модель электронного цифрового частотомера служит для измерения частоты и периода периодических электрических сигналов.
Ниже приведены некоторые метрологические характеристики модели:
• диапазон рабочих частот от 10 Гц до 10 МГц;
входное напряжение не менее 3 В не более 10 В;
входное сопротивление не менее 1 МОм.

Генератор сигналов синусоидальной формы. [1, стр.19]
Модель генератора сигналов синусоидальной формы служит для формирования гармонического электрического сигнала с регулируемыми параметрами.
Ниже приведены некоторые метрологические характеристики модели:
диапазон рабочих частот от 1 Гц до 100 кГц;
выходное напряжение плавно регулируется в диапазоне от 0 В до 5 В;

погрешность установки частоты выходного сигнала не более 1 %.
Электронный аналоговый резонансный частотомер. [1, стр.20]
Модель электронного аналогового резонансного частотомера служит для измерения частоты гармонических электрических сигналов.
Ниже приведены некоторые характеристики модели:
• диапазон рабочих частот от 1 Гц до 100 кГц;
• класс точности обозначен 1, следовательно, предел допускаемой
приведенной погрешности равен 1%;
• входное сопротивление не менее 1 МОм.
• входное напряжение не менее 20 мВ и не более 10 В.

4. Расчетные формулы
4.1 Связь оценок погрешности (неопределенности) измерений частоты и периода.
Так как частота
 и период
и период
 связаны соотношением
связаны соотношением
 , [1,
ф.7.1]
, [1,
ф.7.1]
то, зная оценку погрешности (неопределенности) одного параметра, легко оценить погрешности (неопределенности) другого, воспользовавшись методикой оценки погрешности (неопределенности) косвенных измерений [1 – 7]

 , [1,
ф.7.2]
, [1,
ф.7.2]
или
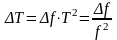 , [1,
ф.7.3]
, [1,
ф.7.3]
где
 - граница абсолютной погрешности
(неопределенности) измерения периода;
- граница абсолютной погрешности
(неопределенности) измерения периода;
 - граница абсолютной
погрешности (неопределенности) измерения
частоты.
- граница абсолютной
погрешности (неопределенности) измерения
частоты.
Перейдя
к относительным неопределенностям
периода
 и частоты
и частоты
 ,
получим:
,
получим:
 . [1,
ф.7.4]
. [1,
ф.7.4]
4.2 Оценка погрешности (неопределенности) измерения частоты цифровым частотомером.
Относительная
погрешности (неопределенности) измерения
частоты частотомером
складывается
из двух компонентов: относительной
погрешности (неопределенности) частоты
образцового (обычно кварцевого) генератора
частотомера
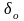 и относительной погрешности
(неопределенности) дискретизации
(квантования)
и относительной погрешности
(неопределенности) дискретизации
(квантования)
 ,
вызванной тем, что аналоговую величину
представляют целым числом импульсов
,
вызванной тем, что аналоговую величину
представляют целым числом импульсов

 . [1,
ф.7.5]
. [1,
ф.7.5]
Значение задано в метрологических характеристиках частотомера, вычисляют, пользуясь выражением
 [1,
ф.7.6]
[1,
ф.7.6]
где
 - измеренное значение частоты;
- измеренное значение частоты;
 - время счета,
установленное на частотомере.
- время счета,
установленное на частотомере.
Исходя из (7.5):
 . [1,
ф.7.7]
. [1,
ф.7.7]
4.3. Оценка погрешности (неопределенности) измерения периода
цифровым периодомером.
Относительная погрешности (неопределенности) измерения периода периодомером складывается из трех компонентов: относительной погрешности (неопределенности) частоты образцового (обычно кварцевого) генератора прибора , относительной погрешности (неопределенности) уровня запуска (формирования), вызванной наличием шумов в исследуемом сигнале и нестабильностью порога срабатывания формирующего устройства и относительной погрешности (неопределенности) дискретизации (квантования) , вызванной тем, что аналоговую величину представляют целым числом импульсов .
Предел допускаемой относительной погрешности измерения периода оценивают по формуле
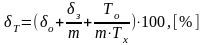 [1,
ф.7.8]
[1,
ф.7.8]
где - относительная погрешность (неопределенность) частоты образцового (обычно кварцевого) генератора частотомера, она указана в метрологических характеристиках прибора;
 - относительная
погрешность (неопределенность) уровня
запуска (формирования), вызванная
наличием шумов в исследуемом сигнале
и нестабильностью порога срабатывания
формирующего устройства в периодомере,
она указана в метрологических
характеристиках прибора;
- относительная
погрешность (неопределенность) уровня
запуска (формирования), вызванная
наличием шумов в исследуемом сигнале
и нестабильностью порога срабатывания
формирующего устройства в периодомере,
она указана в метрологических
характеристиках прибора;
 - период следования
образцовых (счетных) импульсов,
установленный на периодомере, эти
импульсы иногда называют тактовыми или
метками времени;
- период следования
образцовых (счетных) импульсов,
установленный на периодомере, эти
импульсы иногда называют тактовыми или
метками времени;
m - множитель периода исследуемого сигнала, установленный на периодомере (коэффициент деления частоты исследуемого сигнала);
 - измеренное
значение периода.
- измеренное
значение периода.
Следовательно, погрешность уровня запуска измерения периода равна
 ,
а погрешность дискретизации
,
а погрешность дискретизации
 .
[1, стр.17]
.
[1, стр.17]
4.4 Оценка погрешности (неопределенности) измерения частоты
резонансным частотомером.
Для
резонансного частотомера, используемого
в лабораторной работе, нормирован предел
допускаемой приведенной погрешности
.
В этом случае предел допускаемой
абсолютной погрешности измерения
частоты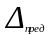 находят по формуле:
находят по формуле:
 ,
[1, стр.17]
,
[1, стр.17]
где
 – нормирующее значение, равное конечному
значению шкалы частот установленного
на частотомере частотного диапазона.
Предел допускаемой относительной
погрешности находят из соотношения:
– нормирующее значение, равное конечному
значению шкалы частот установленного
на частотомере частотного диапазона.
Предел допускаемой относительной
погрешности находят из соотношения:
 ,
[1, стр.17]
,
[1, стр.17]
где
 – измеренное значение частоты (показание
частотомера).
– измеренное значение частоты (показание
частотомера).
Задачи для контроля самостоятельной работы.
Решение предложенных измерительных задач необходимо привести в заготовке отчета до начала занятия.
ЗАДАЧА
1. Определить частоты (
или
 ),
абсолютную и относительную погрешности
(неопределенности) и форму сигналов на
входах «Х» и «Y»
осциллографа, если на его экране наблюдают
фигуру, показанную в таблице 5.1, а частота
сигнала и его абсолютная погрешности
(неопределенности)
на одном из входов осциллографа
соответствует таблице 5.2. Оформите
результаты измерений в соответствии с
нормативными документами.
),
абсолютную и относительную погрешности
(неопределенности) и форму сигналов на
входах «Х» и «Y»
осциллографа, если на его экране наблюдают
фигуру, показанную в таблице 5.1, а частота
сигнала и его абсолютная погрешности
(неопределенности)
на одном из входов осциллографа
соответствует таблице 5.2. Оформите
результаты измерений в соответствии с
нормативными документами.
Таблица 5.1 Фигуры Лиссажу к задаче 1
Последняя цифра номера студенческого билета (пароля) |
2 |
|
Таблица 5.2 Значение частоты и ее абсолютной погрешности (неопределенности) к задаче 1
Вид параметра |
Предпоследняя цифра номера студенческого билета (пароля) |
2 |
|
, Гц |
40 |
, Гц |
? |
, Гц |
4 |
Если
фигура на экране осциллографа неподвижная,
справедливо соотношение
 [2, стр.207]
[2, стр.207]
Где fy-частота сигнала поданного на вход Y осциллографа
fx- частота сигнала поданного на вход X осциллографа
 -максимальное
число пересечений наблюдаемой фигуры
Лиссажу с горизонтальной секцией
-максимальное
число пересечений наблюдаемой фигуры
Лиссажу с горизонтальной секцией
 -максимальное
число пересечений наблюдаемой фигуры
Лиссажу с вертикальной секцией
-максимальное
число пересечений наблюдаемой фигуры
Лиссажу с вертикальной секцией

В данном случае




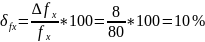
Ответ:

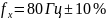
P=0,997 Условия измерения нормальные.
Изобразим формы сигналов X и Y

ЗАДАЧА
2. Определить показание периодомера
(градуировка в миллисекундах), абсолютную
и относительную погрешности
(неопределенности) дискретности измерения
периода и число импульсов, накопленное
в электронном счетчике цифрового
периодомера при измерении периода
сигнала, частота которого
 указана в таблице 5.3, если частота
следования счетных импульсов
указана в таблице 5.3, если частота
следования счетных импульсов
 и коэффициент деления делителя частоты
исследуемого сигнала (множитель периода)
и коэффициент деления делителя частоты
исследуемого сигнала (множитель периода)
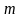 в периодомере соответствуют таблице
5.5.
в периодомере соответствуют таблице
5.5.
Таблица 5.3 Частота исследуемого сигнала к задаче 2
Вид параметра |
Последняя цифра номера студенческого билета (пароля) |
2 |
|
, Гц |
400 |
Таблица 5.4 Частота следования счетных импульсов и коэффициент деления делителя частоты исследуемого сигнала (множитель периода) к задаче 2
Вид параметра |
Предпоследняя цифра номера студенческого билета (пароля) |
2 |
|
|
10 |
|
10 |
Определим период

Найдем относительную погрешность дискретности измерения периода

Где



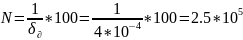
Ответ:
 ,
,
 ,
N=
,
N=
Показание
периодомера
 мс
мс
ЗАДАЧА
3. Известны: показание частотомера,
частота и относительная нестабильность
частоты опорного кварцевого генератора
 (см. таблицу 5.6). Выполнить задание,
указанное в таблице 5.7.
(см. таблицу 5.6). Выполнить задание,
указанное в таблице 5.7.
Таблица 5.6 Показание частотомера, частота опорного генератора
и нестабильность его частоты к задаче 3
Предпоследняя цифра номера студенческого билета |
Показание частотомера |
|
Частота опорного генератора, МГц |
2 |
000358,12 кГц |
5 |
1 |
Таблица 5.7 Задание к задаче 3
Последняя цифра номера студенческого билета |
З а д а н и е |
2; 7 |
Определить интервал времени, в течение которого был открыт электронный ключ в процессе измерения. |
Решение:
Найдем количество импульсов, поступивших на счетчик

Тогда для показания «000358,12 кГц»
N=35812
Найдем интервал времени

Ответ:

6. Выполнение работы.
6.3 Исследование погрешности (неопределенности) измерения частоты и периода цифровым частотомером.
Таблица 6.1 Значения частоты F1 генератора сигнала при измерении частоты и периода
Варианты |
Последняя цифра номера зачетной книжки (пароля) |
2 |
|
F1, кГц |
0,08 |
Таблица 6.2 Значения частоты F2 генератора сигнала при измерении
частоты и периода
Варианты |
предпоследняя цифра номера зачетной книжки (пароля) |
2 |
|
F2 , кГц |
85 |
Пороговое напряжение равно 3В
Таблица 6.3 Результаты исследования погрешности (неопределенности) измерения частоты цифровым частотомером
Частота генератора сигналов, Гц |
Время счета, с |
Показание частото- мера, кГц |
Абсолютная погрешность дискретизации, Гц |
Относительная погрешность дискретизации, % |
Граница абсолютной погрешности измерения частоты, Гц |
Граница относительной погрешности измерения частоты, % |
Результат измерения частоты; Р=0.997; Условия измерения нормальные |
80 |
1 |
0,081 |
1 |
1,2346 |
1,00012 |
1,2347 |
|
80 |
10 |
0,0801 |
0,1 |
0,124844 |
0,10012 |
0,12499 |
|
85000 |
0,01 |
85.1 |
100 |
0,117647 |
100,01 |
0,117659 |
|
85000 |
1 |
85.001 |
1 |
0,001176471 |
1,12749 |
0,00132646 |
|
85000 |
10 |
85.0000 |
0,1 |
0,000117647 |
0,2275 |
0,000267647 |
|
Найдем относительную погрешность дискретизации:

Найдем абсолютную погрешность дискретизации:
 Гц
Гц
Найдем границу относительной погрешности измерения частоты
.


Найдем границу абсолютной погрешности измерения частоты:


Таблица 6.4 Результаты косвенного измерения периода колебаний частотомером
Частота генератора сигналов, Гц |
Время счета, с |
Показание частото- мера, кГц |
Рассчитанное значение периода, мс |
Граница абсолютной погрешности измерения периода, мкс |
Граница относительной погрешности измерения периода, % |
Результат измерения периода Р=0.997; Условия измерения нормальные |
80 |
1 |
0,081 |
12,3457 |
152,434 |
1,2347 |
|
80 |
10 |
0,0801 |
12,4844 |
15,6047 |
0,12499 |
|
85000 |
0,01 |
85.1 |
0,0117509 |
0,0138097 |
0,117659 |
|
85000 |
1 |
85.001 |
0,0117646 |
0,00015605 |
0,001326457 |
|
85000 |
10 |
85.0000 |
0,0117647 |
0.000031488 |
0,000267647 |
|
Рассчитаем значение периода
,

Перейдя к относительным неопределенностям периода и частоты , получим:
.
Таким
образом:

Найдем границу абсолютной погрешности измерения периода
,

 %
%
6.4 Исследование погрешности (неопределенности) измерения периода и частоты цифровым периодомером.
Таблица 6.5 Результаты исследования погрешности (неопределенности) измерения периода цифровым периодомером
Частота генератора сигналов |
Положение переключателя «множитель периода» |
Положение переключателя периода счетных импульсов, мкс |
Показание периодомера |
Абсолютная погрешность дискретизации, мкс |
Относительная погрешность дискретизации, % |
Граница абсолютной погрешности измерения периода, мкс |
Граница относительной погрешности измерения периода, % |
Результат измерения периода Р=0.997; Условия измерения нормальные |
80 Гц |
1 |
0,01 |
12500,01мкс |
0,01 |
0,0000799999 |
37,5288 |
0,30023 |
|
80 Гц |
1 |
10 |
12,51мс |
10 |
0,0799361 |
47,5488 |
0,38009 |
|
85 кГц |
1 |
0,01 |
11,77мкс |
0,01 |
0,0849618 |
0,0453277 |
0,385112 |
|
85 кГц |
1 |
10 |
0,02мс |
10 |
50 |
10,060 |
50,3002 |
|
80 Гц |
|
10 |
12,5001мс
|
0,1 |
0,000799994 |
0,493753 |
0,00394999 |
|
80 Гц |
|
10 |
2,500001мс |
0,001 |
0,00004 |
0,0055 |
0,00022 |
|
85 кГц |
|
10 |
0,0118мс |
0,1 |
0,847458 |
0,100372 |
0,850608 |
|
85 кГц |
|
10 |
0,011765мс |
0,001 |
0,00849979 |
0,00102118 |
0,00868 |
|
Относительная погрешность дискретизации:
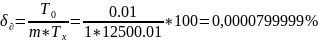
Абсолютная погрешность дискретизации:

Граница относительной погрешности измерения периода:

=0,30023%
 %
%
,гдеδ0=1.5*10-6
δx=3*10-3
Граница абсолютной погрешности измерения периода:

 %
%
Таблица 6.6 Результаты косвенного измерения частоты сигнала периодомером
Частота генератора сигналов |
Положение переключателя «множитель периода» |
Положение переключателя периода счетных импульсов, мкс |
Показание периодомера |
Расчетное значение частоты Гц |
Граница абсолютной погрешности измерения частоты, Гц |
Граница относительной погрешности измерения частоты, % |
Результат измерения частоты Р=0.997; Условия измерения нормальные |
80 Гц |
1 |
0,01 |
12500,01мкс |
79,9999 |
0,240184 |
0,30023 |
|
80 Гц |
1 |
10 |
12,51мс |
79,9361 |
0,303826 |
0,38009 |
|
85 кГц |
1 |
0,01 |
11,77мкс |
84,9618 |
327,198 |
0,385112 |
|
85 кГц |
1 |
10 |
0,02мс |
50 |
25150,1 |
50,3002 |
|
80 Гц |
|
10 |
12,5001мс
|
79,9994 |
0,00315997 |
0,00394999 |
|
80 Гц |
|
10 |
2,500001мс |
400 |
0,00088 |
0,00022 |
|
85 кГц |
|
10 |
0,0118мс |
84,7458 |
720,854 |
0,850608 |
|
85 кГц |
|
10 |
0,011765мс |
84,9979 |
7,37763 |
0,00868 |
|
Найдем значение частоты:


Так как
Граница абсолютной погрешности измерения частоты:

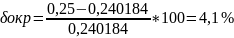


 ,
МГц
,
МГц
 Гц
Гц %
% Гц
Гц Гц
Гц
 %
% кГц
кГц кГц
кГц %
% Гц
Гц Гц
Гц %
% Гц
Гц Гц
Гц %
% мс
мс мс
мс
 %
% мс
мс мс
%
мс
% мкс
мкс %
% нс
нс нс
нс %
% нс
нс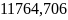 нс
нс %
% мкс
мкс мкс
мкс %
% мкс
мкс мкс
мкс %
% мкс
мкс мкс
мкс %
% с
с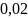 мс
мс %
%
 мкс
мкс %
%
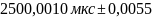 мкс
мкс мкс
мкс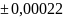 %
% мкс
мкс мкс
мкс %
%
 мкс
мкс %
% Гц
Гц Гц
%
Гц
% Гц
Гц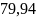 Гц
%
Гц
% Гц
Гц Гц
%
Гц
%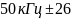 кГц
кГц кГц
%
кГц
% Гц
Гц Гц
Гц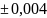 %
% Гц
Гц Гц
%
Гц
% Гц
Гц Гц
%
Гц
% Гц
Гц Гц
%
Гц
%