чм 5

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ»

ЛАБОРАТОРНАЯ РАБОТА №5

«Одномерная оптимизация»

Выполнил: Ядринцев С.М.

Проверил: Сосновиков Г.К.

Москва 2022

1. Выбрать индивидуальное задание по номеру варианта из табл.5-1 для решения задачи одномерной оптимизации:

   • Функцию f(x),минимум которой необходимо найти;

   • метод золотое сечение

   • метод дихотомии

2. Провестиисследованиеиндивидуальноговариантазадания:

   • Построить график функции y=f(x);

   • Выбрать начальный отрезок неопределенности (отрезок, содержащий точку минимума);

   • проверить выполнение аналитического условия унимодальности функции на выбранном отрезке.

3. Ручной расчет

4. Создать в сценарии функцию для проведениязначений 3-х итерацийопределить длину отрезка, содержащего точку минимума, послетрехитераций.

5. Решить задачу оптимизации с использованием функции optim пакета Scilab.

Индивидуальное задание

№ вар.	Целеваяфункция
23	f(x) =

.

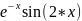
1. Задание для решения задачи одномерной оптимизации:

   • функция, для которой необходимо найти минимум

2. Исследованиезадания:

• график функции отрезке ОДЗ функции:

y=f(x), построенный на достаточно большом

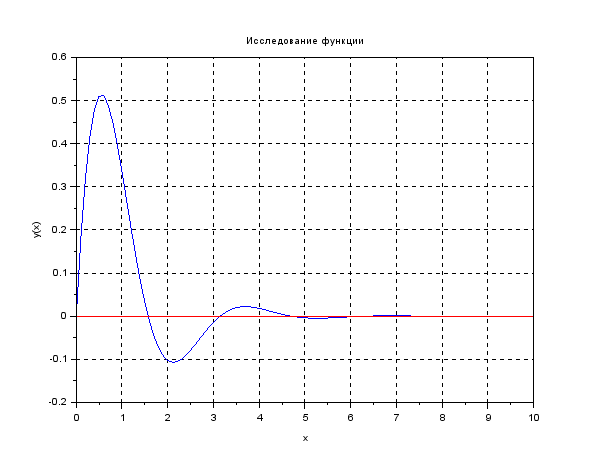
• выберем по построенному графику функции начальный отрезок неопределенности (отрезок, содержащий точку минимума): отрезок[1.5;2.5];

• проверим выполнение аналитического условия унимодальности функции на выбранном отрезке:

function fx=f(x) fx=sin(2*x).*exp(-x); end function dy=f1(x) // первая производная от f(x) dy=numderivative(f, x); endfunction function dy=f2(x) // вторая производная от f(x) dy=numderivative(f1, x); endfunction disp(" x f(x) f`(x) f``(x)"); m=[ ]; for x=1.5:0.1:2.5 z=[x, f(x), f1(x),f2(x)]; m=[m,z']; end disp(m');

" x f(x) f`(x) f ``(x)" 1.5 0.0314881 -0.4732825 0.7891238 1.6 -0.0117855 -0.3913189 0.8415657 1.7 -0.0466831 -0.3065531 0.8465216 1.8 -0.0731481 -0.2233182 0.8123771 1.9 -0.0915147 -0.1450932 0.74776 2. -0.1024221 -0.0745 0.6611105 2.1 -0.1067301 -0.0133411 0.5603326 2.2 -0.1054405 0.0373336 0.4525353 2.3 -0.0996263 0.0771377 0.3438561 2.4 -0.09037 0.1062455 0.2393591 2.5 -0.0787133 0.1252821 0.1430023

Достаточное условие: f ``(x)>0

^{Необходимое условие:} f`(x) пересекает точку 0 (меняет знак с – на +)

На отрезке [1.5;2.5] функция f`(x) монотонно возрастает, следовательно, функции f(x) – на выбранном отрезке унимодальная.

3. Результаты сценария функции трех итераций методом Дихотомии.

Сценарий метода Дихотомии:

function ff=f(x) ff=sin(2*x).*exp(-x); endfunction function d=dih(a, b, d) n=1; k=b-a; m=[]; while n<>4 x1=(a+b)/2-d; x2=(a+b)/2+d; del=(k-2*d)/2^n+2*d; z=[n,a,b,x1,x2,f(x1),f(x2),del]; m=[m,z']; n=n+1; if f(x1)>=f(x2) then a=x1; else b=x2; end end xmin=(a+b)/2; fun=[xmin,f(xmin)] disp(m'); disp("Координаты точки минимума:"); disp(' xmin f(xmin)'); disp(fun); disp('Длина неопределенности отрезка после трех итераций = '); disp(del); end a=1.5; b=2.5; d=0.01; disp("Результат расчета 3 итераций метода Дихотомии:"); disp(" n a b x1 x2 f(x1) f(x2) deln"); dih(a,b,d);

Результаты работы кода:

"Результат расчета 3 итераций метода Дихотомии:" "n a b x1 x2 f(x1) f(x2) deln" 1. 1.5 2.5 1.99 2.01 -0.1016439 -0.1031342 0.51 2. 1.99 2.5 2.235 2.255 -0.1038645 -0.102733 0.265 3. 1.99 2.255 2.1125 2.1325 -0.1068534 -0.1068738 0.1425 4. 2.1125 2.255 "Координаты точки минимума:" " xmin f(xmin)" 2.18375 -0.1059867 "Длина неопределенности отрезка после трех итераций = " 0.1425

n	a	b	х1	х2	f(x1)	f(x2)	deln
1	1.5	2.5	1.99	2.01	-0.1016439	-0.1031342	0.51
2	1.99	2.5	2.235	2.255	-0.1038645	-0.102733	0.265
3	1.99	2.255	2.1125	2.1325	-0.1068534	-0.1068738	0.1425

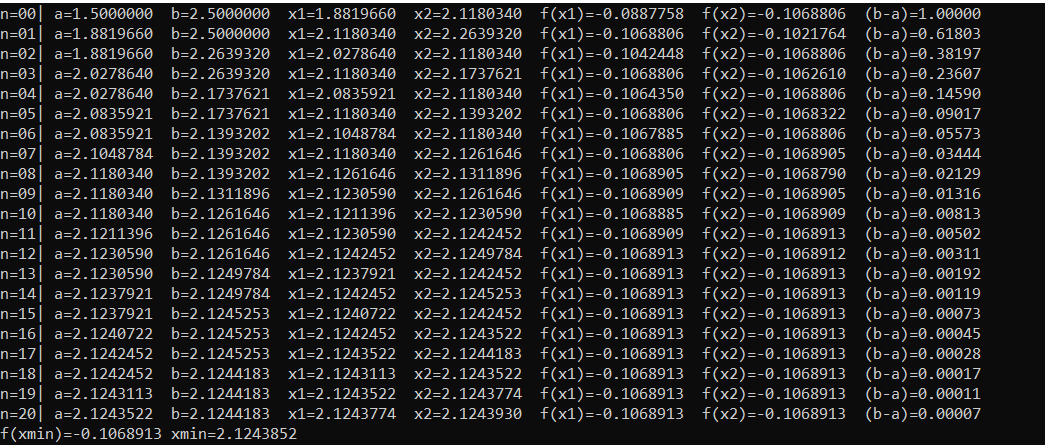
4. Результаты работы программы вычисления координат точки минимума методом Золотого сечения с точностью E=10^-4.

Код С++ Золотого сечения:

#include<iostream> #include<cmath> using namespace std; double fun(double x) { double f = sin(2*x) *exp(-x); return(f); } double sec(double a, double b, double Ex) { int n=0; double xmin; double k1 = (3 - sqrt(5)) / 2; double k2 = (sqrt(5)-1) / 2; double x1 = a + k1 * (b-a); double x2 = a + k2 * (b - a); double F1 = fun(x1); double F2 = fun(x2); printf("n=%.2d| a=%.7f b=%.7f x1=%.7f x2=%.7f", n, a, b, x1, x2); printf(" f(x1)=%.7f f(x2)=%.7f (b-a)=%.5f\n", fun(x1), fun(x2), (b - a)); do { if (F1 < F2) { b = x2; x2 = x1; x1 = a + k1 * (b - a); F2 = F1; F1 = fun(x1); } else { a = x1; x1 = x2; x2 = a + k2 * (b - a); F1 = F2; F2 = fun(x2); } n = n + 1; printf("n=%.2d| a=%.7f b=%.7f x1=%.7f x2=%.7f", n, a, b, x1, x2); printf(" f(x1)=%.7f f(x2)=%.7f (b-a)=%.5f\n", fun(x1), fun(x2), (b - a)); } while ((b-a) > Ex); xmin = (a + b) / 2; return(xmin); } int main() { double a=2, b=3, ex = 0.0001; double xmin=sec(a,b,ex); printf("f(xmin)=%.7f xmin=%.7f", fun(xmin),xmin); }

Результаты работы кода:

5. Число итераций, необходимое для локализации точки минимума и E=10^-4

Теоретическая величина погрешности для метода дихотомии определяется длиной конечного отрезка неопределенности после N итераций .

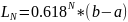Отсюда имеем .

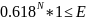Если точность E=0.0001, то получим:

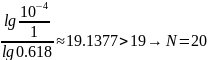
В результате расчета на ПК при N=19 длина отрезка равна 0.00011. Точность достигнута при N=20,т. е. расчет совпадает с теоретической оценкой.

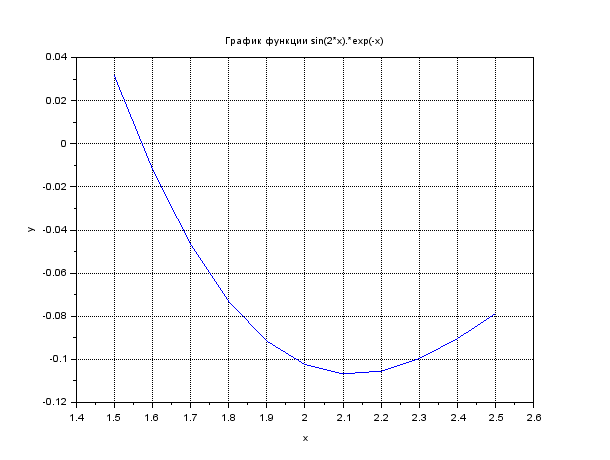
Решение задачи оптимизации с использованием функции optim пакета Scilab.

x=1.5:0.1:2.5; y=sin(2*x).*exp(-x); plot(x, y); xtitle('График функции sin(2*x).*exp(-x)','x','y'); xgrid(); // Решение задачи оптимизации deff('y=f0(x)','y=sin(2*x).*exp(-x)'); //Описание целевой функции function [f, g, ind]=costf(x, ind) f=f0(x) g=numderivative(f0,x) endfunction x0=1.5; [fmin,xmin]=optim(costf,x0); disp('fmin='); disp(fmin); disp('xmin='); disp(xmin); "fmin=" -0.1068913 "xmin=" 2.1243707