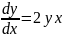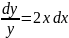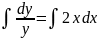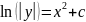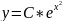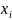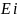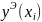чм 4
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ»
ЛАБОРАТОРНАЯ РАБОТА №4
«Методы решения обыкновенных дифференциальных уравнений»
Выполнил: Ядринцев С.М.
Проверил: Сосновиков Г.К.
Москва 2022
Общее задание
Выбрать индивидуальное задание в табл. 4-1 для решения обыкновенных дифференциальных уравнений:
Дифференциальное уравнение y’=f(x,y);
Интервал [a; b], где ищется решение дифференциального уравнения;
начальные условия
,
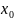;шаг интегрирования
.
Найти аналитическое решение y=y(x) заданного дифференциального уравнения, полагая его точным.
Создать в сценарии функцию для вычисления значения полученного решения y(x) на отрезке [a;b] с шагом .
Создать в сценарии функцию для вычисления значений численное значение решение дифференциального уравнения методом Эйлера -
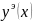в точках отрезка
[a;b]
с шагом
.Вычислить значение погрешностей
для
,
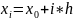.Написать и выполнить программу, реализующую программу решения дифференциального уравнения методом Рунге-Кутта 4-го порядка
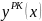в точках отрезка
[a;b]
с шагом
,
обеспечив с использованием метода
автоматического выбора шага, точность
10-4.Вычислить значение погрешностей
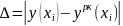для
,
.Найти решения дифференциального уравнения
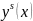использованием функции пакета Scilab
ode.Проиллюстрировать решение
,
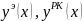в одной системе координат.
Индивидуальный вариант задания
Задание для численного решения обыкновенных дифференциальных уравнений:
Дифференциальное уравнение
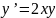
Интервал [0; 0.6];
начальные условия
,
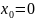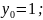шаг
интегрирования
.
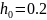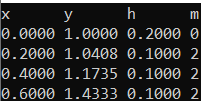
Точное аналитическое решение заданного дифференциального уравнения:
Найдем точное аналитическое решение заданного дифференциального уравнения (решение y=y(x)).
Из начальных условий следует, что C = 1.
Аналитическое
решение дифференциального уравнения
примет вид
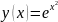
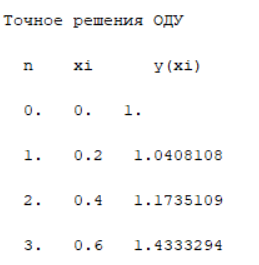
Значение точного решения ОДУ -
:
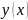n |
|
|
0 |
0 |
1 |
1 |
0.2 |
1.0408108 |
2 |
0.4 |
1.1735109 |
3 |
0.6 |
1.4333294 |
//Сценарий точного решения ОДУ function y=resh(x, n) function y=func(x) y=exp(x.^2); end disp('Точное решения ОДУ'); disp(' n xi y(xi)'); for i=1:n+1 y(i)=func(x(i)); z=[i-1,x(i),y(i)] disp(z); end endfunction |
|
Численное решение ОДУ методом Эйлера:
n |
|
|
0 |
0 |
1 |
1 |
0.2 |
1 |
2 |
0.4 |
1.08 |
3 |
0.6 |
1.2528 |
//Сценарий численного решение ОДУ методом Эйлера function y=eler(x, h, n) function yy=func(x, y) yy=2*x.*y; end x(1)=0; y(1)=1; disp('Численное решение ОДУ методом Эйлера'); disp(' n xi yЭ(xi)'); z=[0,x(1),y(1)]; disp(z); for i=2:n+1 y(i)=y(i-1)+h*func(x(i-1),y(i-1)); z=[i-1,x(i),y(i)] disp(z); end endfunction |
|
Значение погрешностей:
n |
|
|
0 |
0 |
0 |
1 |
0.2 |
0.0408108 |
2 |
0.4 |
0.0935109 |
3 |
0.6 |
0.1805294 |
//Сценарий погрешности точного решения и Эйлера function E=pogrel(x, n, yr, ye) disp('Погрешность между точным решением и методом Эйлера'); disp(' n xi Ei'); for i=1:n+1 E(i)=abs(yr(i)-ye(i)); z=[i-1,x(i),E(i)] disp(z); end endfunction |
|
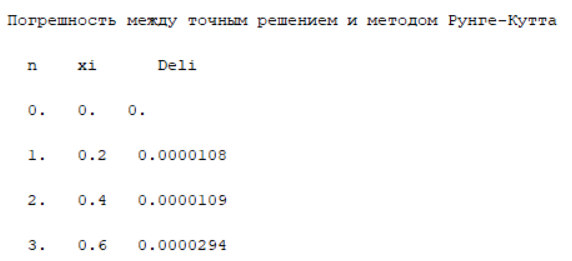
Результаты решения ОДУ методом Рунге-Кутта 4-го порядка, дополненным методом автоматического выбора шага, обеспечивающим точность 10-4:
n |
|
|
0 |
0 |
1 |
1 |
0.2 |
1.0408 |
2 |
0.4 |
1.1735 |
3 |
0.6 |
1.4333 |
//код решения ОДУ #include<iostream> #include<cmath> using namespace std;
double fun(double x, double y) { double f =2*x*y; return(f); }
double r(double x, double y, double h, int m) { double k1, k2, k3, k4; for (int j = 1; j <= m; j++) { k1 = fun(x, y); k2 = fun(x + h / 2, y + h * k1 / 2); k3 = fun(x + h / 2, y + h * k2 / 2); k4 = fun(x + h, y + h * k3); y = y + (h / 6) * (k1 + 2 * k2 + 2 * k3 + k4); x = x + h; } return(y); }
void diff(double x0, double y0, double h0, double Ex, double b)
{ int n, i, m = 0; double h, y, y1, x; n = (b - x0) / h0+1; cout << "x y h m\n"; printf("%.4f %.4f %.4f %d \n", x0, y0, h0, m); for (int j = 1; j <= n; j++) { h = h0; m = 1; y = r(x0, y0, h, m); do { y1 = y; h = h / 2; x = x0; y = y0; m = 2 * m; y = r(x, y, h, m); } while (abs(y - y1) > Ex); x0 = x0 + h0; y0 = y; printf("%.4f %.4f %.4f %d \n", x0, y0, h, m); } }
int main() { double x0 = 0, y0 = 1, h0 = 0.2, ex = 0.0001, b = 0.6; diff(x0, y0, h0, ex, b); } |
|
Значение погрешностей
:
|
|
|
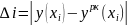0 |
0 |
0 |
1 |
0.2 |
0.0000108 |
2 |
0.4 |
0.0000109 |
3 |
0.6 |
0.0000294 |
//Сценарий погрешности точного решения и Рунге-Кутта function del=pogrk(x, n, yr, yrk) disp('Погрешность между точным решением и методом Рунге-Кутта'); disp(' n xi Deli'); for i=1:n+1 del(i)=abs(yr(i)-yrk(i)); z=[i-1,x(i),del(i)] disp(z); end endfunction |
|
Все решения полученные выше
|
|
|
|
|
|
0 |
1 |
1 |
0 |
1 |
0 |
0.2 |
1.0408108 |
1 |
0.0408108 |
1.0408 |
0.0000108 |
0.4 |
1.1735109 |
1.08 |
0.0935109 |
1.1735 |
0.0000109 |
0.6 |
1.4333294 |
1.2528 |
0.1805294 |
1.4333 |
0.0000294 |
Решение ОДУ с использованием функции ode пакета Scilab:
function yd=f(t, y)
yd=2*t.*y;
endfunction
y=1; t0=0; t=0:0.2:0.6;
z=ode(y,t0,t,f);
disp('Решение ОДУ функцией ode');
zz=[t;z];
disp(zz');
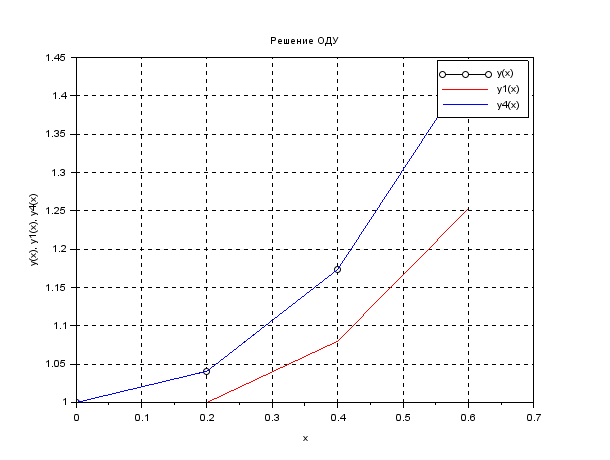
Все решения в одной системе координат:
//Сценарий вызова других функций и построения графиков a=0; b=0.6; h=0.2; n=(b-a)/h; for i=1:n+1 x(i)=a+(i-1)*h; end yr=resh(x,n); ye=eler(x,h,n); pogrel(x,n,yr,ye); yrk=evstr(x_dialog('Ведите значения оду в точках по Рунге_Кутту','')); pogrk(x,n,yr,yrk'); plot(x,yr,'k-o'); plot(x,ye,'r-'); plot(x,yrk','b-'); xgrid(); xtitle('Решение ОДУ','x','y(x), y1(x), y4(x)'); legend('y(x)','y1(x)','y4(x)'); |
