лабы / другие лабы / механика / laba5(2)
.docОбнинский Государственный Технический Университет Атомной Энергетики.
ФИЗИКО-ЭНЕРГЕТИЧЕСКИЙ ФАКУЛЬТЕТ.
Кафедра общей и специальной физики.
Лабораторная работа № 5.
Тема:
«Изучение поступательного движения на машине Атвуда».
Выполнил: Ермаков А. С.
Проверил: Вишератин К. Н.
Обнинск 2001
Цель работы:
Изучение поступательного движения на машине Атвуда, определение ускорения свободного падения опытным путем.
Перечень оборудования:
Машина Атвуда.
Краткая теория.
Поступательное движение тела описывается основным уравнением динамики:
ma=F (1)
Закон движения тела:
x=x0+(at)2/2
Таким образом второй закон Ньютона запишется в виде:
Ma1=Mg – T1
(M+m)a2=(M+m)g – T2 (3).
Основное уравнение вращательного движения:
I
=
rT1’+rT2’-N
(4).
Поскольку масса нити много меньше масс грузов, её можно считать невесомой, тогда:
T1=T1’ и T2=T2 (5)’
Если считать, что нить нерастяжима и не
проскальзывает по блоку, то: -a1=a2=a
(6)
Угловое и линейное ускорение связаны соотношением:
a= r (7)
Решив совместно систему 3-7 получим:
a=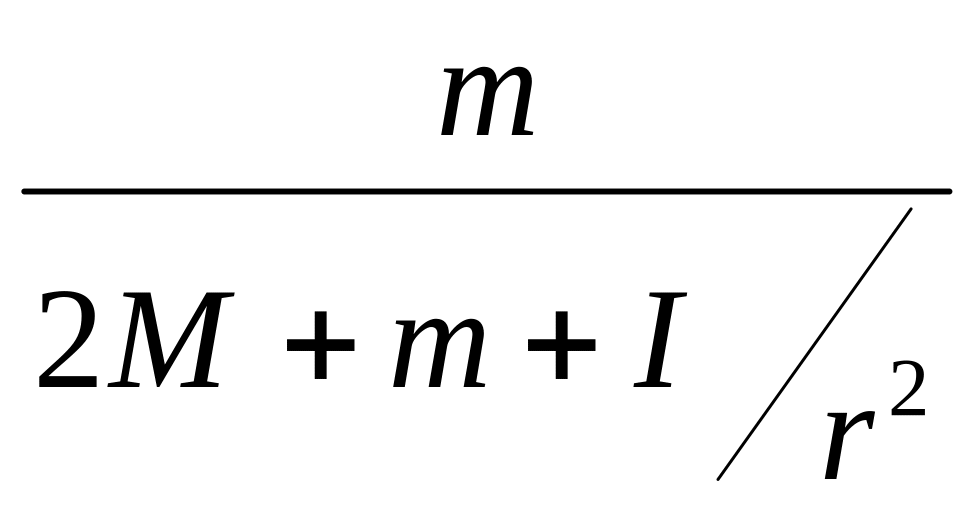
g
-
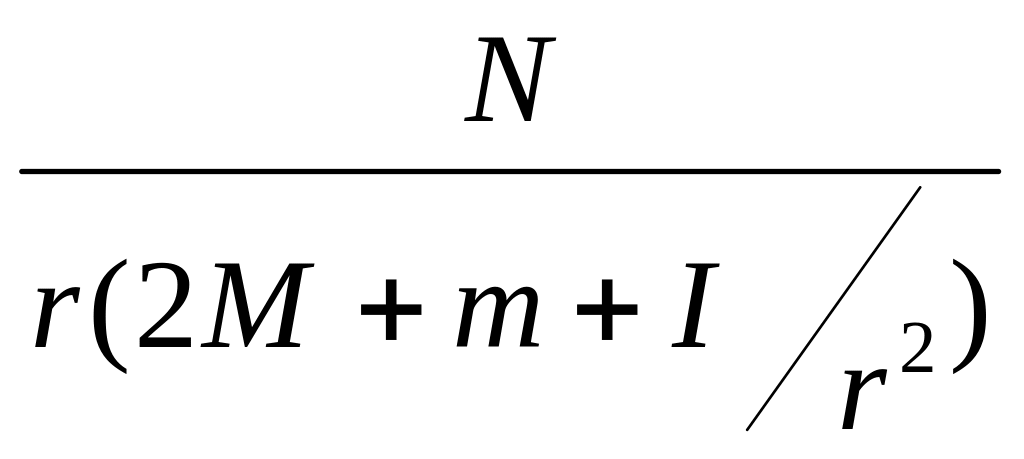(8)
Для ускорения свободного падения g получим:
g=
(9)
Если не учитывать момент инерции блока и момент сил трения, ускорение свободного падения можно определить по приближенной формуле:
g=
(10)
Полученное таким образом значение g окажется заниженным. К нему следует добавить поправку:
(11)
Момент сил трения можно определить экспериментально. Помещая на правый груз малые перегрузки, определить массу перегрузка m0 , при которой начнется движение грузов. Тогда N=rm0g (12)
С учетом (12) выражение для поправки примет вид:
(13)
В нашей работе ускорение свободного падения определяется по формуле (10) с учетом поправки (13).
Ускорение, используемое в формуле (10), получают в соответствии с законом равноускоренного движения (2):
a=
, (14)
где L определяется, как L=x – x0
Относительная погрешность для a (она является косвенно измеренной величиной) вычисляется следующим образом:
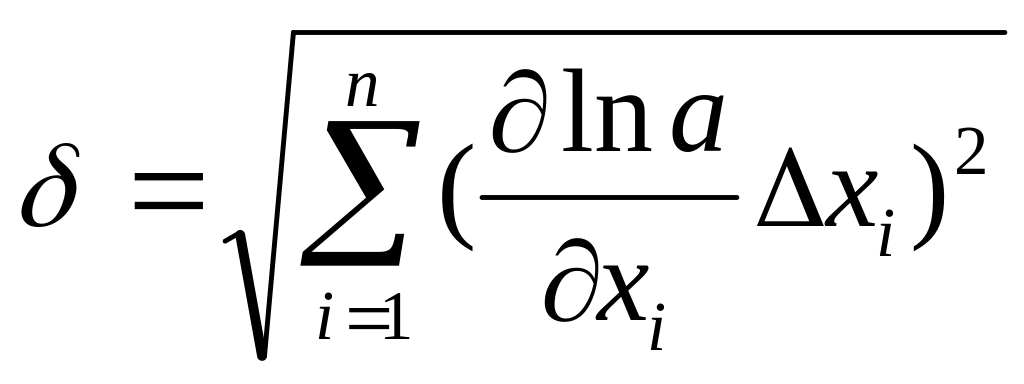
lna=ln =ln2L – lnt2= ln2L - 2lnt ,
(15)
Абсолютная погрешность времени
вычисляется
по формуле
(16),
где
мм
= 10-3 м, I=5,77*10-6
кг*м2 , r=41,5 мм ,
M=68,3 г.
Выполнение работы.
I. Включил прибор в сеть и прогрел в течение 5 мин.
II. На правый груз положил один из перегрузков и измерил время, в течение которого груз прошел путь L равный 37 см. Для трех перегрузков повторяем опыт 10 раз. Результату заношу в таблицу №1.
Время:
Таблица №1.
Масса |
m1=4 г |
m2=2.99 г |
m3=1.88 г |
Nопыта |
t1 ,c |
t2 ,c |
t3 ,c |
1 |
1.797 |
2.188 |
2.950 |
2 |
1.727 |
2.209 |
2.958 |
3 |
1.703 |
2.195 |
2.884 |
4 |
1.734 |
2.190 |
2.955 |
5 |
1.713 |
2.191 |
2.911 |
6 |
1.729 |
2.200 |
2.919 |
7 |
1.724 |
2.227 |
2.943 |
8 |
1.715 |
2.203 |
2.955 |
9 |
1.735 |
2.198 |
2.922 |
10 |
1.725 |
2.201 |
2.874 |
< t > |
1.730 |
2.200 |
2.927 |
Ускорение:
Таблица №2.
Масса |
m1=4 г |
m2=2,99 г |
m3=1,89 г |
|
|
|
|
N |
a1i, |
a2i, |
a3, |
|
|
|
|
1 |
0,229 |
0,155 |
0,085 |
|
0,000325 |
2,92 |
1,8 |
2 |
0,248 |
0,151 |
0,0845 |
|
8,40 |
1,48 |
3,24 |
3 |
0,255 |
0,153 |
0,0889 |
|
6,33 |
5,25 |
6,73 |
4 |
0,246 |
0,154 |
0,084 |
|
1,17 |
2,04 |
2,66 |
5 |
0,252 |
0,154 |
0,0873 |
|
2,48 |
1,65 |
9,06 |
6 |
0,247 |
0,152 |
0,0868 |
|
1,17 |
7,6 |
2,24 |
7 |
0,2489 |
0,149 |
0,0854 |
|
3,17 |
1,34 |
7,72 |
8 |
0,251 |
0,152 |
0,0847 |
|
1,93 |
1,51 |
2,66 |
9 |
0,246 |
0,153 |
0,0866 |
|
1,86 |
9,36 |
8,73 |
10 |
0,248 |
0,152 |
0,0895 |
|
2,22 |
1,24 |
1,03 |
<a> |
0,247 |
0,152 |
0,0863 |
Sn |
0,00222 |
0,0005 |
0,00057 |
|
0,0063 |
0,0041 |
0,0018 |
|
1.237 |
2.38 |
3.07 |
III. Нахожу ускорения грузов по формуле a= . Результаты заношу в таблицу №2.
Нахожу среднее значение ускорений:
<a1>=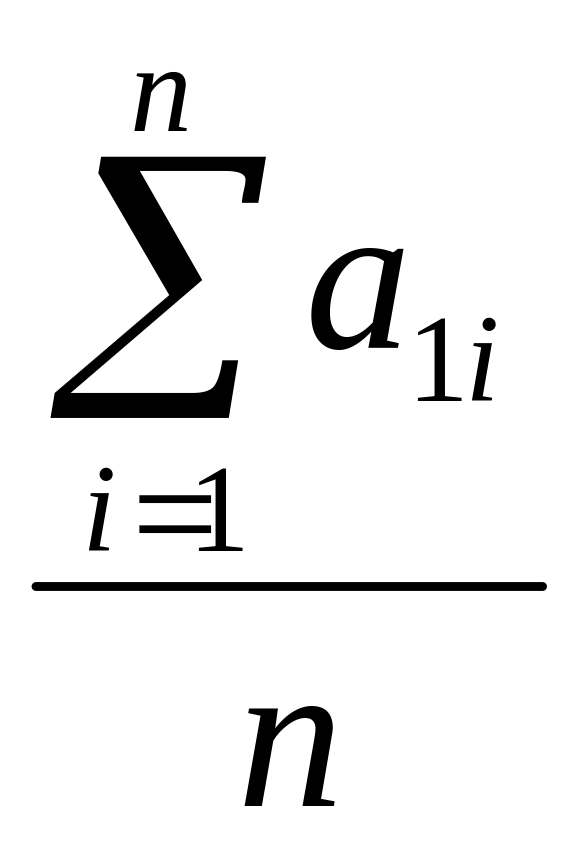
=
0,247
(
)
<a2>=
=
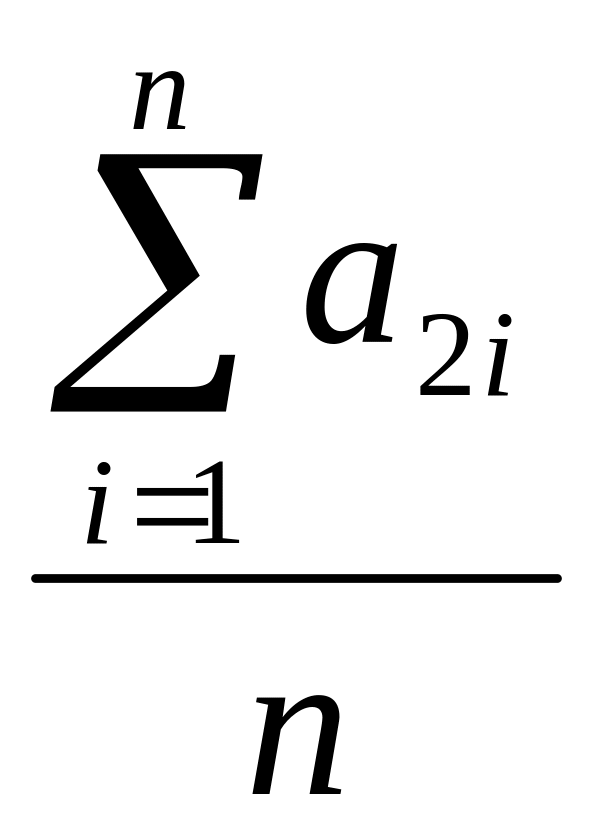0,152
(
)
<a3>=
=
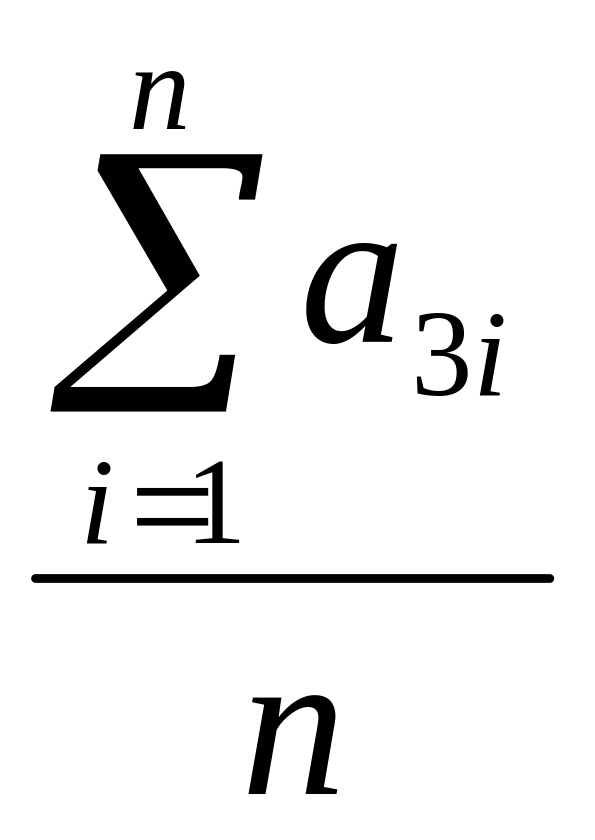0,0863
(
)
Среднее значение времени t=
<t1>= 1,730 с
<t2>= 2,200 с
<t3>= 2,927 с
IV. Нахожу относительные погрешности для ускорений
=
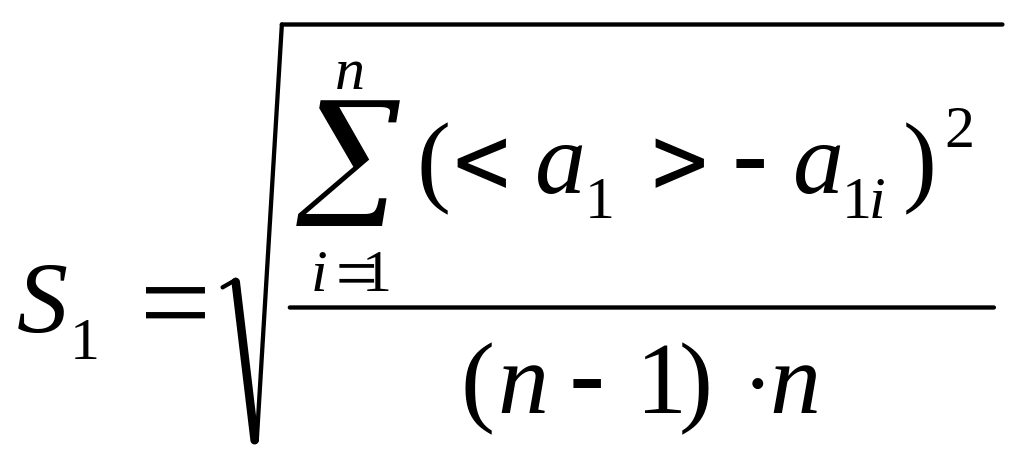0,00222 
=
0,0005
=
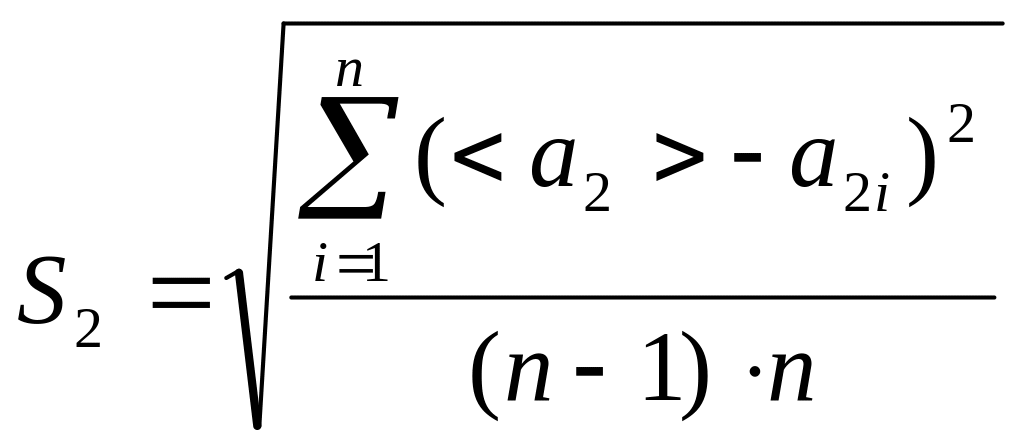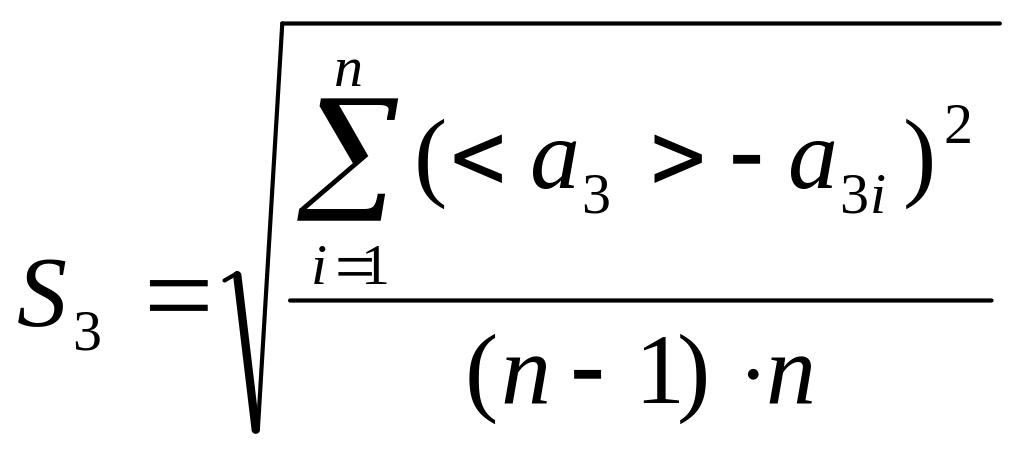0,00057
Ускорения можно записать в виде:
a1 =
0,247
0,00222
a2
= 0,152
0,0005
a3
= 0,0863
0,00057
V. Экспериментально мы установили, что система приходит в равновесие при массе перегрузка m0=420*10-6 кг.
Определим поправку (формула 13):
(
)
(
)
(
)
VI. Вычислим приближенное значение g по формуле 10:
g1=
(
)
g2=
(
)
g3=
(
)
VII. С учетом поправки получаем полное g:
g1=8,69 +1,237 = 9,925 ( )
g2=7,236 +2,38 = 9,616 ( )
g3=6,46 + 3,07 = 9,53 ( )
Таким образом среднее значение g:
<g>=
;
<g>= 9,69 (
)
Погрешность вычисления g:
,
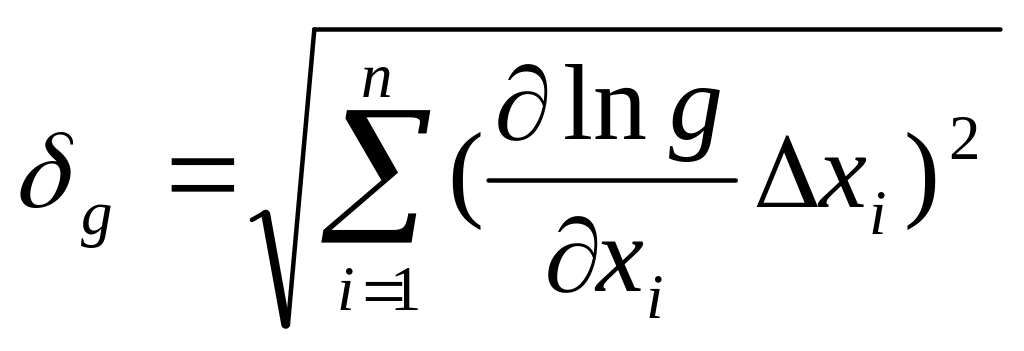где g=
,
причем
Тогда
=
,
=
= 0,231 (
)
Таким образом конечный результат представим в виде:
g=9,69 0,231 ( )
Вывод:
Ознакомился с машиной Атвуда. С помощью этой машины экспериментально определил ускорение свободного падения, которое получилось равным
g=9,69 0,231 ( )