Обнинский Государственный Технический Университет Атомной Энергетики.

ФИЗИКО-ЭНЕРГЕТИЧЕСКИЙ ФАКУЛЬТЕТ.

Кафедра общей и специальной физики.

Лабораторная работа №9.

Тема: Определение скорости полета пули с помощью баллистического маятника.

Выполнил: Ермаков А. С.

Принял: Вишератин К. Н.

Обнинск 2002.

Цель работы:

С помощью баллистического крутильного маятника определить импульс и энергию пули; по полученным данным установить скорость полета пули, научится вычислять погрешности, допускаемые при работе.

Оборудование:

Баллистический крутильный маятник, пуля в форме полого цилиндра.

Краткая теория:

Погрешности различных приборов измерения:

Систематическая погрешность миллисекундомера Δt=5 мс.

Систематическая погрешность измерения расстояния до пули ∆L=0,5 мм

Систематическая погрешность измерения угла отклонения 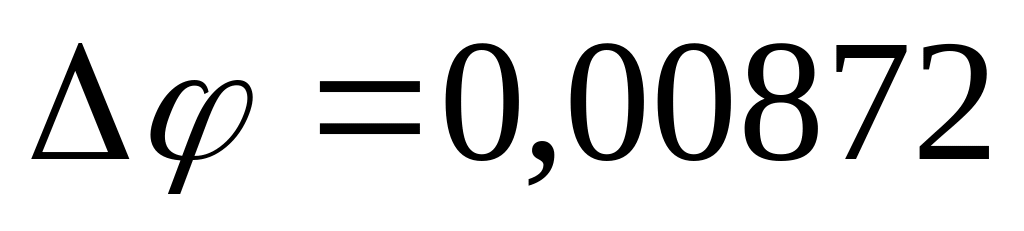рад

Масса грузов М=181,3  0,1 г. Масса пули m = мг.

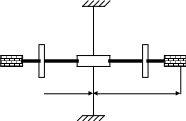Выведем формулы для

O’ вычесления скорости пули:

Момент импульса в системе

пуля-маятник сохраняется:

M M (I₁+mL²) - mVL=0 (1)

где I₁ и mL^{2 .}

- моменты инерции маятника и

пули относительно оси ОО’.

 - угловая скорость маятника

R L вместе с пулей сразу же после

удара; m , V – масса и скорость

O пули.

Если принебречь работой неконсервативных сил сопротивления при движении маятника, то полная механическая энергия остается постоянной:

(2) , где - потенциальная энергия упругой деформации стальной нити в момент максимального отклонения маятника от положения равновесия (G- модуль сдвига стальной нити, характеризующий ее упругие свойства, - угол поворота маятника, выраженный в радианах); - кинетическая энергия системы сразу после удара, когда нить подвеса еще не закручена.

Решая совместно (1) и (2), получим: (3). Так как момент инерции пули mL² много меньше момента инерции маятника I₁, то выражение (3) можно переписать в следующем виде: Таким образом, зная массу пули m и измеряя угол ₀ и расстояние L можно определить начальную скорость пули.

Найду G записав для двух моментов инерции маятника I₁ и I₂ соответствующие периоды колебаний: (6) и (7). Различные моменты инерции получаем располагая грузы на расстояниях R₁ и R₂. Пусть I_0M – момент инерции груза М относительно оси, проходящей через его центр масс и параллельной оси вращения маятника. Тогда момент инерции груза относительно оси OO’ есть I_OM+MR². Тогда получаем: I₁=I₀+2I_OM+2MR₁² (8) I₂=I₀+2I_OM+2MR₂² (9) где I₀ –момент инерции маятника без грузов М. Из уравнений (6) (7) (8) (9) получаем 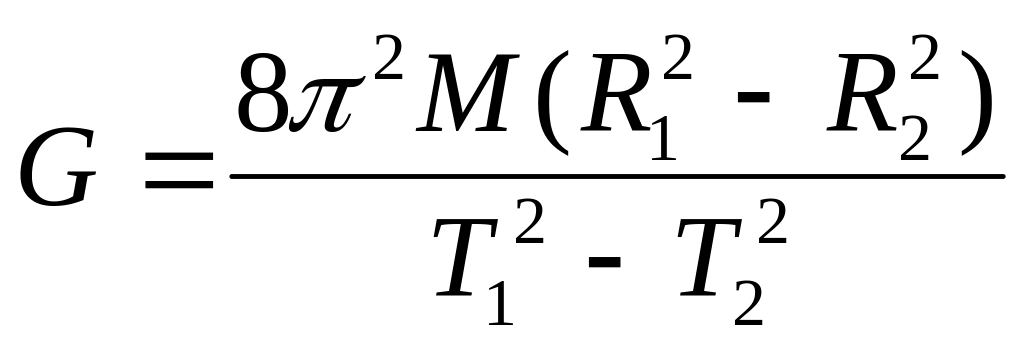(10) и 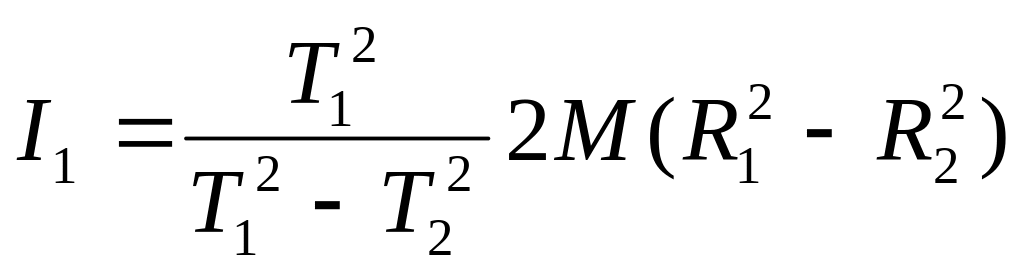(11) подставляя выражения из (10) и (11) в уравнение (4), получаем окончательную формулу для вычисления скорости полета пули:

Выполнение работы.

Таблица.

№	град	L мм	рад	При R1= см T1= с
				При R2= см T2= с

I. Переведу значение угла из градусов в радианы по формуле и заношу результаты в таблицу.

II. Используя результаты измерений, я вычисляю среднее значение длинны и величены угла по формуле: (где ).

< >= рад

<L>= мм

III. Определю средние квадратичные погрешности средних значений по формуле:

;

= рад = мм

IV. Затем я вычисляю абсолютную погрешность измерений: , где - систематическая погрешность, определяемая точностью измерительного инструмента, а - случайная погрешность. Случайная погрешность вычисляется по формуле (a = 0.95); Коэффициент Стьюдента t=2.3. Его взял из таблицы для случая доверительной вероятности =0.95, n=10.

= рад; = мм

рад; мм

Вычисляю относительную погрешность измерений: ,

; = * 10; ; ; ;

Ответ для максимального угла отклонения: рад

Ответ для расстояния от центра масс до положения пули: мм

Вычисляю скорость полета пули V: по формуле

Откуда м/c

Вычислю относительную погрешность для скорости: ∆V= ,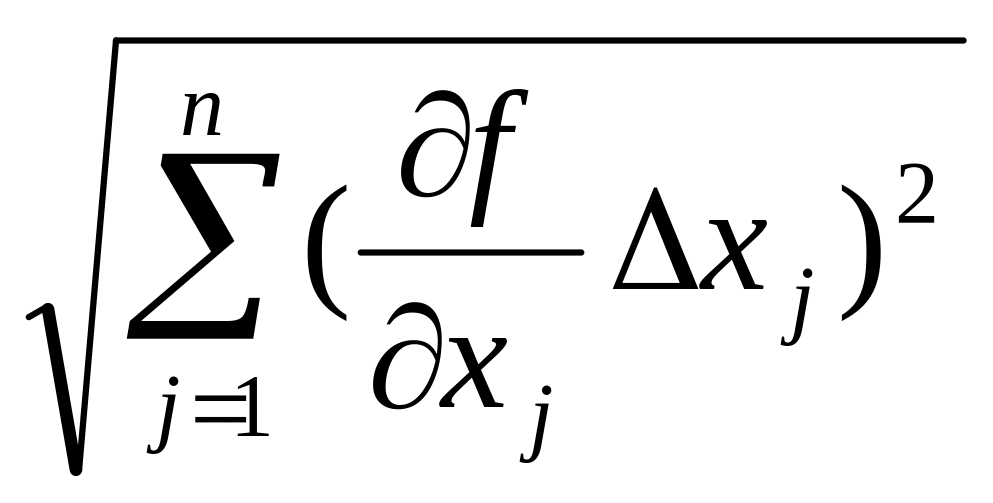

где

= м/c

Ответ: V=( ± ) м/c

Вывод: В результате проведенных опытов я нашел скорость пули. Анализируя полученный результат, видим, что такая скорость пули в данных условиях возможна. Следовательно, при проведение работы не было допущено грубых измерительных и вычислительных ошибок.