
лабы / другие лабы / механика / Лаб 6
..docМинистерство Общего и Специального Образования
Обнинский Институт Атомной Энергетики
Кафедра общей и специальной физики
Лабораторная работа N6.
Тема:
«Изучение вращательного движения твердого тела вокруг неподвижной оси на примере маятника Обербека».
Выполнил: Казанцев С.
Бодунов С.
Тихонов А.
Группа А1-01
Проверила: Лескина Надежда Николаевна
Обнинск 2001
Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси имеет следующий вид:
I![]() =Nвнеш
,
=Nвнеш
,
где - угловое ускорение тела, Nвнеш- сумма проекций на эту ось моментов всех внешних сил, приложенных к телу , I-момент инерции твердого тела относительно оси.
В работе вращательное движение твердого тела изучается на приборе, называемом маятником Обербека.
С учетом момента сил трения Nтр в оси подшипника шкива уравнение примет вид:
I =N-Nтр,
где N=T’r-момент силы натяжения нити,T’=T – сила натяжения нити, r-радиус шкива.
Цель работы: изучение вращательного движения на примере маятника Обербека.
Задание 1.
Экспериментальная проверка основного уравнения вращательного движения, определение момента инерции системы и оценка влияния момента силы трения.
Время падения груза, массой m
Nопыта |
t0 (m1=58,3) |
t1 (m2=50,6) |
T2 (m3=50,9) |
|
1 |
5,921 |
4,318 |
3,566 |
h=38,3 см |
2 |
5,833 |
4,342 |
3,541 |
R=7,2 см |
3 |
5,903 |
4,321 |
3,561 |
r=2,3 |
По
формуле <x>=![]() найдем
среднее значение времени падения.
найдем
среднее значение времени падения.
<t0>=5,855
<t1>=4,327
<t2>=3,556
По
формуле Sn=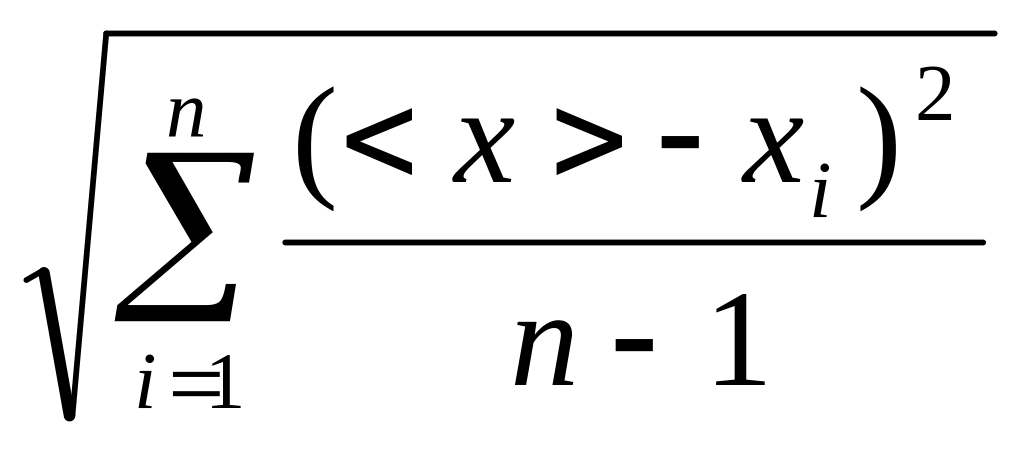 и S=
и S=![]() найдем погрешности единичных измерений
Sn
и S:
найдем погрешности единичных измерений
Sn
и S:
Sn, t0=0,041 (c) ; St0=0,023 (c)
Sn, t1=0,013 (c) ; St1=0,007 (c)
Sn, t2=0,013 (c) ; St2=0,007 (c)
По
формуле
![]() найдем абсолютную погрешность t:
найдем абсолютную погрешность t:
![]() (
(![]() ,
т.е.
,
т.е.
![]() )
)
По
формуле
![]() найдем случайную погрешность пи измерении
t (ta,n=4,3,
a=0,95, n=3)
найдем случайную погрешность пи измерении
t (ta,n=4,3,
a=0,95, n=3)
![]() =0,023*4,3=0,09
(c)
=0,023*4,3=0,09
(c)
![]() =0,03
(c)
=0,03
(c)
![]() =0,03
(c)
=0,03
(c)
По
формуле
![]() найдем угловое ускорение
найдем угловое ускорение
<
>=
(
1+
2+
3)*![]()
1=0,949 c-2; 2=0,978 c-2; 3=0,955 c-2;
< 0>=0,960 c-2
Аналогично:
< 1>=1,778 c-2
< 2>=2,633 c-2
По
формуле
![]() найдем относительную погрешность
косвенных измерений
:
найдем относительную погрешность
косвенных измерений
:
![]() :
ln
=ln2h-2lnt-lnr
=
lnh-2lnt-lnr
:
ln
=ln2h-2lnt-lnr
=
lnh-2lnt-lnr
![]() =
=![]()
(![]() =10,5
(мм); r=2,3
0,2
(см)); т.е.
=10,5
(мм); r=2,3
0,2
(см)); т.е.![]() 0,0013
0,0013
![]()
![]() =0,08
=0,08
т.е.:
![]() =0,08
=0,08
Аналогично:
![]() 0,08
0,08
![]() 0,08
0,08
По
формуле
![]() найдем абсолютную погрешность
:
найдем абсолютную погрешность
:
![]() с-2
с-2
![]() с-2
с-2
![]() с-2
с-2
т.е.:
0=0,96 0,07=(9,6 0,7)*10-1 с-2=(96 7)*10-2 с-2
1=(177 14)*10-2 с-2
2=(263 21)*10-2 с-2
По
формуле
![]() найдем
момент силы натяжения:
найдем
момент силы натяжения:
<N0>=58,3*10-3
кг*(9,8-0,022)![]() *2,3*10-3=0,0130
Н*м
*2,3*10-3=0,0130
Н*м
<N1>=0,0241 Н*м
<N2>=0,0353 Н*м
По
формуле
![]() =
=![]() рассчитаем
относительную погрешность косвенных
измерений N:
рассчитаем
относительную погрешность косвенных
измерений N:
lnN=lnM+ln(g-![]() )+lnr
)+lnr
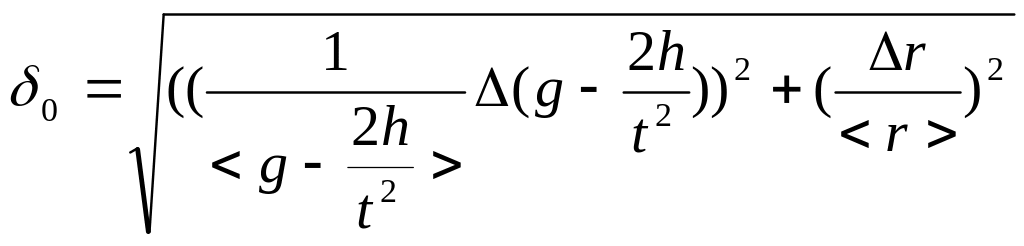 =
=![]()
<g-
>=9,76;
![]() =0,0008
=0,0008
![]() =8,1*10-5
=8,1*10-5
![]() 0
0
т.е.
относительной погрешностью
![]() можно пренебречь, т.е.:
можно пренебречь, т.е.:
![]() =0,08
=0,08
![]()
![]() =0,08
=0,08
![]() =0,08
=0,08
т.е.:
![]() Н*м
Н*м
![]() Н*м
Н*м
![]() =
0,0028 Н*м
=
0,0028 Н*м
N0=0,013 0,001 Н*м=(1,3 0,1)*10-2 Н*м=(13 1)*10-3 Н*м*с2
N1=0,0241 0,0019 Н*м=(24 2)*10-3 Н*м*с2
N2=(35 3)*10-3Н*м*с2
Как видно из этого графика Nтр=0,19*10-2 Н*м, т.е. им можно пренебречь
J=ctg![]() =
=![]() =0,0127
Н*м*c2
=0,0127
Н*м*c2
Задание 2.
Проверка теоремы Штейнера.
Nопыта |
t1 (r=12см) |
t2 (r=9см) |
|
1 |
7,640 |
6,576 |
h=38,3 |
2 |
7,567 |
6,521 |
|
3 |
7,714 |
6,529 |
|
По
формуле J=Mr2(![]() )
определяем J
)
определяем J
Для :
<t1>=7,641 c; Snt1=0,07 c; St1=0,04 c
![]() =0,04*4,3=0,17
=0,04*4,3=0,17
<t2>=6,542 c; Snt2=0,029 c; St2=0,016 c
![]() =0,06
=0,06
(h=38,3 0,5 см; r=2,3 0,2 см) 0,0013; 0,08
<J1>=58,3*10-3*(2,3*10-2)2*(![]() =0,023
Н*м*с2
=0,023
Н*м*с2
<J2>=58,3*10-3*(2,3*10-2)2*(![]() =0,0168
Н*м*с2
=0,0168
Н*м*с2
По формуле = рассчитаем относительную погрешность косвенных измерений момента инерции маятника:
lnJ=lnM+2lnr+ln( )
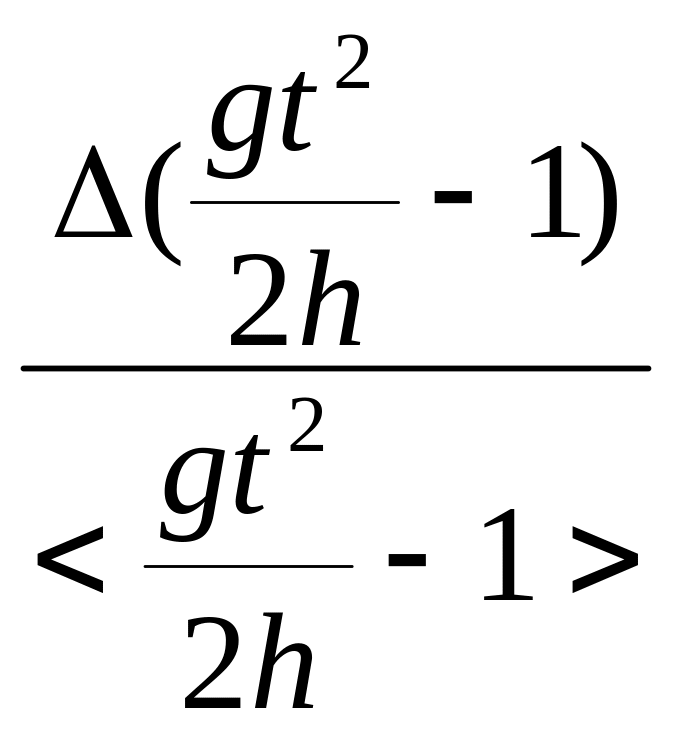 0
т.е.
0
т.е.
![]() =2
=2![]()
1= 2=2*0,08=0,16
т.е.
![]() =0,003
Н*м*с2
=0,003
Н*м*с2
![]() =0,0026
Н*м*с2
, т.е.
=0,0026
Н*м*с2
, т.е.
J1=0,023 0,003=(23 3)*10-3 Н*м*с2
J2=(17 3)*10-3
Как видно из графика
(J(0))=0,69*10-2 Н*м*с2
Время движения платформы при снятых грузах m:
Nопыта |
t,c |
1 |
4,292 |
2 |
4,229 |
3 |
4,300 |
<t>=4,233
c; Snt=0,03
c; St=0,017c;
![]() =0,07
c
=0,07
c
![]() =0,016
=0,016
Определим момент инерции Jкр маятника без грузов m:
<Jкр>=58,3*10-3*(2,3*10-2)2*(![]() =0,00703
Н*м*с2
=0,00703
Н*м*с2
![]() =0,16
=0,16
![]() =0,16*0,00703=0,001
Н*м*с2
=0,16*0,00703=0,001
Н*м*с2
т.е. Jкр=0,007 0,001=(7 1)*10-2 Н*м*с2
Т.к. по теореме Штейнера J=J(0)+4mR2
J(0)=Jкр+4J0
![]() J(0)
J(0)![]() Jкр
Jкр
J(0)=0,69*10-2 H*м*с2
Jкр=(0,7 0,1)*10-2
По формуле найдем J0 – момент инерции груза массой m относительно оси, проходящей через его центр масс и параллельной оси, вокруг которой вращается маятик.
(L=2
см;
m=200,7;
![]() ;
;
![]() =0,3
см )
=0,3
см )
J0=2,7*10-3 Н*м*с2
ВЫВОД: В первом задании при построении графика экспериментальной точки, в пределах точности измерений, “легли” на прямую. Это подтверждает зависимость
![]() (N-
момент силы натяжения нити)
(N-
момент силы натяжения нити)
Из графика было найдено J=0,013 Н*м*с2. Причем порядок J совпадает с числом величин J1 и J2 высчитанных во втором задании по экспериментальным данным. Это также подтверждает правильность построения графиков.
Во втором задании были определены моменты инерции тела J1 и J2. Был построен график зависимости J(R), причем как в первом задании, график-прямая, т.е. подтверждается зависимость J=J(0)+4mR2.
А также из графика было найдено J(0) 0,69*10-2 Н*м*с2
