лабы / другие лабы / молекулярка / Лабораторная Работа 5

Обнинский Институт Атомной Энергетики.

ФИЗИКО-ЭНЕРГЕТИЧЕСКИЙ ФАКУЛЬТЕТ.

Кафедра общей и специальной физики.

Тема: Изучение распределения Гаусса и двумерного

распределения Максвелла на механической модели.

Cдал: Егоров.Е.С

Принял:Фесенко.Г.А

Случайные явления часто встречаются в физике и технике, например, при многократных измерениях физических величин, при стрельбе в цель, при изучении теплового движения молекул,

радиоактивного распада и т.д. Предсказать результат отдельного случайного явления невозможно, на нём сказывается влияние большого числа факторов, не поддающихся контролю. Случайные явления описываются с помощью теории вероятности и статистических законов, дающих возможность определить вероятность, с которой осуществляется то или иное событие в серии случайных событий, наиболее вероятные и средние значения этих величин, стандартные отклонения и т.п. Для подобного рода вычислений необходимо знать закон или функцию распределения. Для очень широкого класса физических явлений таким законом является закон Гаусса или нормальное распределение Гаусса .Это распределение имеет место в том случае, если случайная величина зависит от большого числа факторов, могущих вносить с равной вероятностью положительные и отрицательные отклонения. Закон нормального распределения имеет вид (1).На рисунке 1 показан график распределения Гаусса; на нём представлены две кривые с разными мерами точности, причём h1>h2. Чем больше мера точности ,тем меньше разброс результатов измерений относительно их среднего значения и выше точность измерений. Важной характеристикой случайной величины является её среднее квадратичное отклонение от среднего  (2) или стандартное отклонение.

Р исунок 1 Дисперсия распределения вычисляется по фор-

f(x) муле (3).С учётом этого, распределение Гаусса

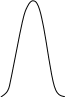имеет вид (4). Определение меры точности h

h1 данной серии случайных величин распределяю-

щихся по нормальному закону, состоит в том,

чтобы найти такое h, при котором появление да-

нной серии величин было бы наиболее вероят-

ным. Вероятность P появления серии случайных

величин равна произведению вероятностей появ

ления каждой из этих величин (5).Мера точно-

h2 сти h определяется из условия максимума веро

ятности P (6).Для стандартного отклонения  и

дисперсии D получим соответственно (7) и (8) .

x

Распределение Максвелла задаёт распределение молекул газа по скоростям при их хаотическом

тепловом движении.Случайные столкновения молекул при их движении в газе приводит к слу

чайным же изменениям их скоростей как по величине так и по направлению.Скорость молекул

удобно изобразить точкой в 3-х мерном пространстве скоростей.Совокупность скоростей всех

молекул газа заполнит пространство скоростей с некоторой плотностью, пропорциональной

плотности вероятности нахождения того или иного значения скорости.Вдоль любого направле-

ния в пространстве скоростей случайные отклонения в ту или иную сторону равновероятны,

поэтому в качестве функции распределения для этого направления можно взять распреде-

ление Гаусса.

Распределение Максвелла по компонентам скоростей (9). Распределение Максвелла по моду

лю скорости (10).На рисунке 2 показана механическая модель с помощью которой право-

дится опыт.

-4 -3 -2 -1 0 1 2 3