
Обнинский Институт Атомной Энергетики
Кафедра Общей и Специальной Физики
Отчет по лабораторной работе №8
«Изучение кратковременного взаимодействий на примере соударения шаров»
Выполнил: Пениос Марк Викторович
Студент группы ИС-Б21
Обнинск 2021
Цель работы: Проверить справедливость закона сохранения импульса при абсолютно упругом соударении и вычислить коэффициент восстановления К.
Оборудование: Экспериментальная установка для изучения соударения шаров.
Ход работы:
1.
Отвести правый шар массы m1=108,2±0,06
г. на угол
 =
15°, затем нажать кнопку пуск для
столкновения с шаром массы m2=173,2±0,06
г.
=
15°, затем нажать кнопку пуск для
столкновения с шаром массы m2=173,2±0,06
г.
Определить
углы
 и
и
 отклонения
шаров после соударения, записать их
значения в таблицу 1. Записать также
показания микросекундомера.
отклонения
шаров после соударения, записать их
значения в таблицу 1. Записать также
показания микросекундомера.
Измерения повторим 10 раз.
Длина нити L = 0,49 м.
Таблица 1. Результаты измерений.
№ опыта |
|
|
t, мкс |
1 |
1,25 |
11 |
107 |
2 |
1 |
11 |
111 |
3 |
1,25 |
11,25 |
111 |
4 |
1,25 |
11,25 |
103 |
5 |
1 |
10,5 |
108 |
6 |
1 |
11 |
104 |
7 |
0,75 |
10,5 |
119 |
8 |
1,25 |
10,75 |
116 |
9 |
1,25 |
11 |
109 |
10 |
1,25 |
11 |
106 |
2.
Вычислим коэффициент восстановления
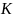 и
модуль средней силы
и
модуль средней силы
 по
формулам:
по
формулам:


Чтобы
найти
 и
и
 нужно
найти скорость тела до и после соударения
по формуле
нужно
найти скорость тела до и после соударения
по формуле

Результаты вычислений заносим в таблицу.
Таблица 2. Результаты вычислений п.2
-
№ опыта
K
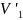

F, кН
1
0,816
0,05
0,005
0,9
2
0,8
0,04
0,004
0,87
3
0,83
0,05
0,005
0,9
4
0,83
0,05
0,005
0,9
5
0,76
0,04
0,004
0,87
6
0,8
0,04
0,004
0,87
7
0,75
0,03
0,003
0,86
8
0,8
0,05
0,005
0,86
9
0,816
0,05
0,005
0,87
10
0,816
0,05
0,005
0,87
3. Оценим погрешности для и по формулам







Таблица 3. Результаты вычислений п.3
|
|
|
|
|
|
|
1,125 |
0,5 |
0.36 |
0.62 |
0.55 |
|
10,925 |
0,68 |
0,5 |
0.70 |
0.06 |
|
109,4 |
12.93 |
9.4 |
9.41 |
0.08 |
|
15 |
0 |
0 |
0,5 |
0,03 |
Погрешность для коэффициента восстановления:




Относительная погрешность:

Абсолютная погрешность:

K= ±
± =0.85±0.44
=0.85±0.44
Погрешность для силы:


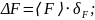

Относительная погрешность:

Абсолютная погрешность:

F=
± =1,98±0,22кН.
=1,98±0,22кН.
Примеры коэффициентов восстановления других материалов
Соударяющиеся тела |
Коэффициент восстановления |
Дерево о резину |
0,26 |
Деревянные шары |
0,5 |
Стеклянные шары |
0,94 |
Кость |
0,89 |
Вывод: В лабораторной работе мы вычислили, что коэффициент восстановления после соударения металлических шаров равен К = 0,85 ± 0,44. Таким образом можно сделать вывод, что соударения были упругими.
Вычислили силу, с которой шары взаимодействовали друг с другом при столкновении F=1,98±0,22кН.
Контрольные вопросы:
1. Абсолютно неупругий удар – это удар, в результате которого обе частицы «слипаются» и далее движутся как единое целое(или это удар, после которого тела имеют одну и ту же скорость или покоятся).
Абсолютно упругий удар – это столкновение в результате которого внутренняя энергия частиц не меняется, а поэтому не меняется и кинетическая энергия системы.
2. Удар называется центральным, если шары до удара движутся вдоль прямой, проходящей через их центры. При центральном ударе соударение может произойти, если: 1) шары движутся навстречу друг другу 2)один из шаров догоняет другой.
3. Fвнеш ∙ ∆t = ∆p— закон изменения импульса системы тел. Импульс суммы внешних сил равен изменению импульса системы тел.
4. Сложим эти два
выражения с учётом того, что
![]() :
:
![]()
![]()
То есть полное
изменение кинетической энергии двух
частиц – это работа внешних сил над
первой частицей, работа внешних сил над
второй частицей и работа силы их
взаимодействия, изменяющая расстояние
между этими частицами. Величина
![]() –
изменение потенциальной энергии двух
частиц. Следовательно, полученное
выражение можно записать следующим
образом:
–
изменение потенциальной энергии двух
частиц. Следовательно, полученное
выражение можно записать следующим
образом:
![]() ,
,
5. Полная механическая энергия системы материальных точек равна:
![]() ,
,
где
![]() –
суммарная кинетическая энергия частиц
системы;
–
суммарная кинетическая энергия частиц
системы;
![]() –
суммарная потенциальная энергия частиц
системы;
–
суммарная потенциальная энергия частиц
системы;
![]() –
суммарная потенциальная энергия
взаимодействия частиц системы между
собой. Коэффициент
–
суммарная потенциальная энергия
взаимодействия частиц системы между
собой. Коэффициент
![]() в
выражении
появился
вследствие того, что суммируется энергия
взаимодействия первой частицы со второй
и второй частицы с первой, но это одна
и та же величина.
в
выражении
появился
вследствие того, что суммируется энергия
взаимодействия первой частицы со второй
и второй частицы с первой, но это одна
и та же величина.








